初中数学浙教版九年级上册第3章 圆的基本性质3.5 圆周角教案配套课件ppt

这是一份初中数学浙教版九年级上册第3章 圆的基本性质3.5 圆周角教案配套课件ppt，文件包含第1课时圆周角定理及其推论1pptx、第2课时圆周角定理的推论2pptx、35圆周角doc、电子教案第1课时圆周角定理及其推论1doc、电子教案第2课时圆周角定理的推论2doc等5份课件配套教学资源，其中PPT共40页， 欢迎下载使用。

1.直径所对的圆周角是直角2.90°的圆周角所对的弦是直径. （重点、难点）
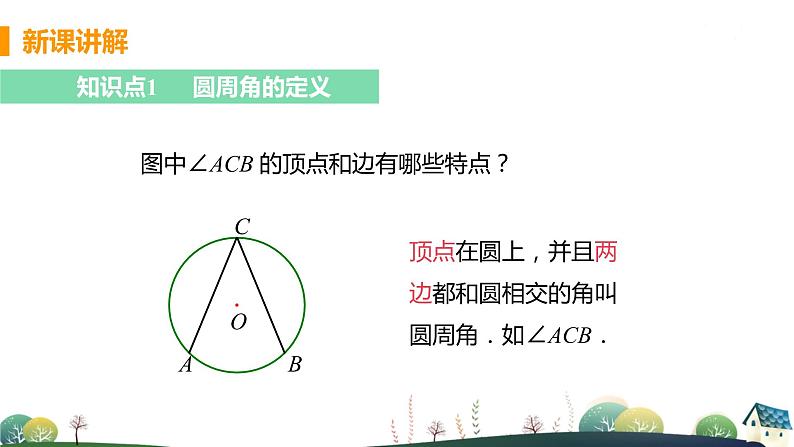
复习回顾1.什么叫做圆周角？2.圆周角定理是什么？3.圆周角定理的推论1的内容是什么？
知识点1 直径所对的圆周角是直角
直径所对的圆周角是多少度？请说明理由.
直径所对的圆周角是直角.
如图所示，已知经过原点的⊙ P 与x 轴、y 轴分别交于A，B 两点，点C 是弧AB 上一点，则∠ ACB 的度数是（ ）A. 80° B. 90°C. 100° D. 无法确定
利用“直角所对的弦是直径”，结合“直径所对的圆周角是直角”求解.
连接AB，如图所示.∵∠ AOB=90°，∴ AB 是⊙ P 的直径.∴∠ ACB=90°.
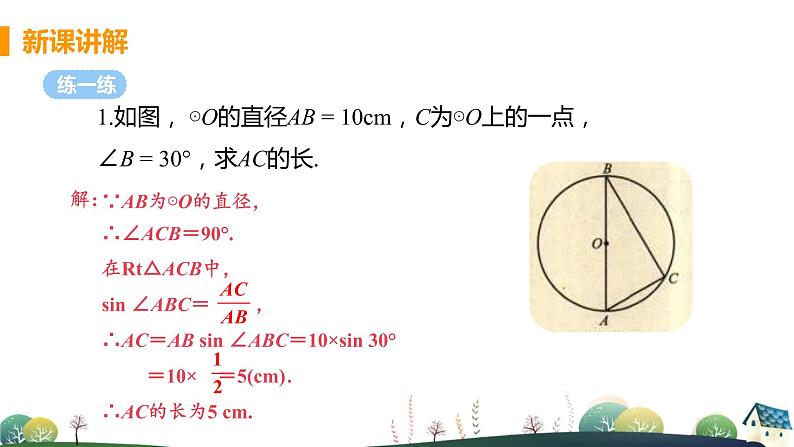
1.如图， ⊙O的直径AB = 10cm，C为⊙O上的一点，∠B = 30°，求AC的长.
∵AB为⊙O的直径，∴∠ACB＝90°.在Rt△ACB中，sin ∠ABC＝ ，∴AC＝AB sin ∠ABC＝10×sin 30° ＝10× ＝5(cm)．∴AC的长为5 cm.
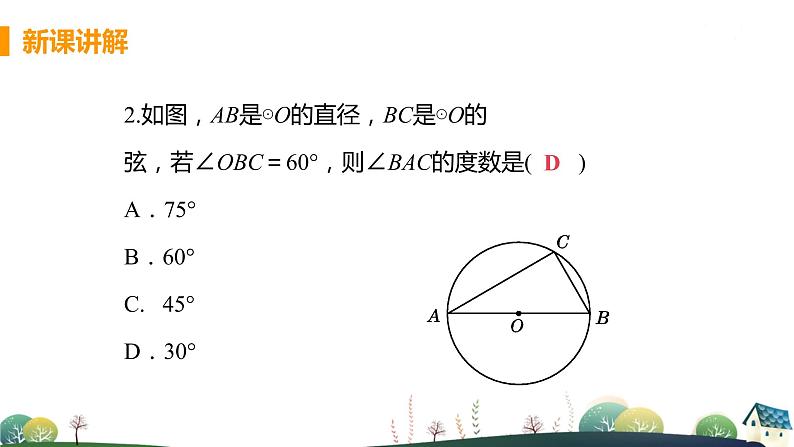
2.如图，AB是⊙O的直径，BC是⊙O的弦，若∠OBC＝60°，则∠BAC的度数是(　　)A．75°　　　B．60°　　　C. 45°　　　D．30°
知识点2 直角所对的弦是直径
在如图中，圆周角∠A＝90°，弦BC是直径吗？为什么？
90°的圆周角所对的弦是直径.
如图，已知经过原点的⊙P与x轴、y轴分别交于A，B两点，点C是劣弧OB上一点，则∠ACB等于(　　)A．80° B．90°　　C．100°　D．无法确定
由∠AOB与∠ACB 是优弧AB所对的圆周角，根据圆周角定理，即可求得∠ACB =∠AOB= 90°.
∵∠AOB与∠ACB 是优弧AB所对的圆周角，∴∠AOB =∠ACB，∵ ∠AOB = 90°，∴ ∠ACB = 90°.
小明想用直角尺检査某些工件是否恰好为半圆形.下面所示的四种圆弧形，你能 判断哪个是半圆形？为什么?
题图(2)是半圆形．∵90°的圆周角所对的弦是直径．
1.已知直径时，常添加辅助线构造直角三角形，即“见直径想 直角”．题目中遇到直径时要考虑直径所对的圆周角为90°， 遇到90°的圆周角时要考虑直角所对的弦为直径，这是圆中 作辅助线的常用方法．2.在解决圆的有关问题时，常常利用圆周角定理及其推论进行 两种转化：一是利用同弧所对的圆周角相等，进行角与角之 间的转化，二是将圆周角相等的问题转化为弦相等或弧相等 的问题.
1.如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD＝30°，则∠BAD为(　　)A．30° B．50° C．60° D．70°
2.如图，已知经过原点的⊙P与x轴，y轴分别交于点A，B，C是劣弧OB上一点，则∠ACB等于(　　)A．80°B．90°C．100°D．无法确定