







初中数学第3章 圆的基本性质3.5 圆周角精品ppt课件
展开3.5圆周角(1) 教案
课题 | 3.5圆周角(1) | 单元 | 第三单元 | 学科 | 数学 | 年级 | 九年级(上) |
学习 目标 | 1.理解圆周角的概念; 2.掌握圆周角定理及其推论,并能熟练地运用其进行论证和计算; 3.通过圆周角定理的证明,了解分情况证明数学问题的思想方法. | ||||||
重点 | 重点是圆周角定理.
| ||||||
难点 | 圆周角定理的证明要分三种情况讨论,有一定的难度,是本节教学的难点.
| ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
导入新课 | 一、创设情景,引出课题
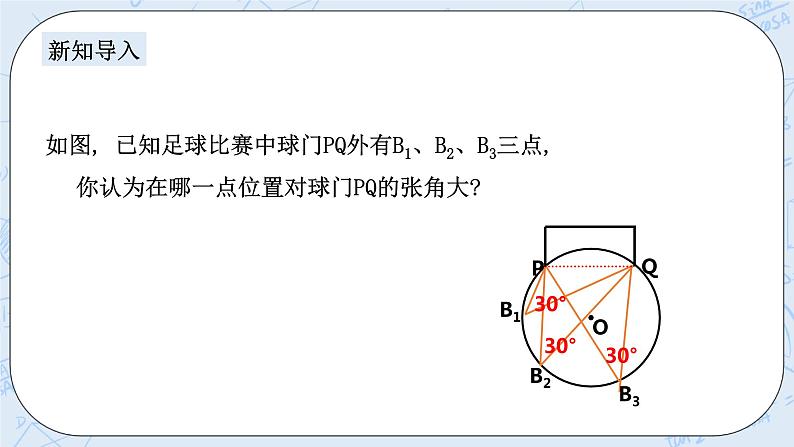
如图, 已知足球比赛中球门PQ外有B1、B2、B3三点,你认为在哪一点位置对球门PQ的张角大?
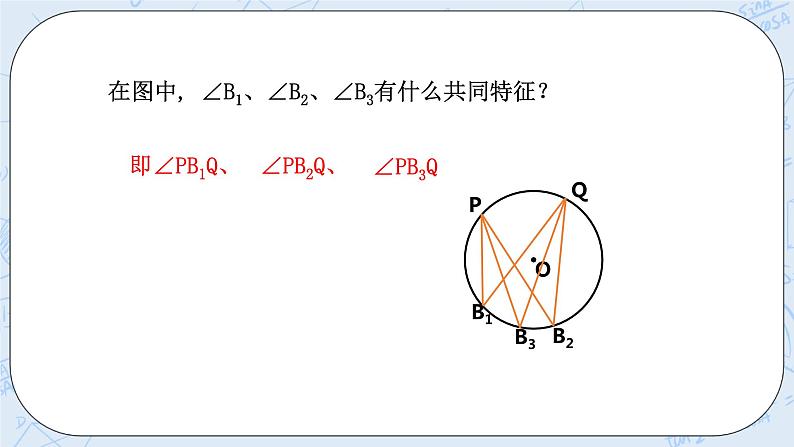
在图中, ∠B1、∠B2、∠B3有什么共同特征? 你能仿照圆心角的定义给圆周角下个定义吗?
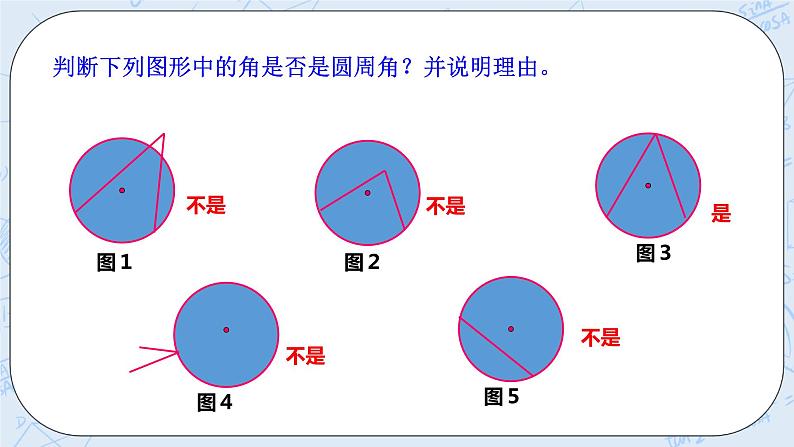
圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角. ① 角的顶点在圆上. ② 角的两边都与圆相交. 辩一辩:下列各图中,哪一个角是圆周角?( ) 探究一
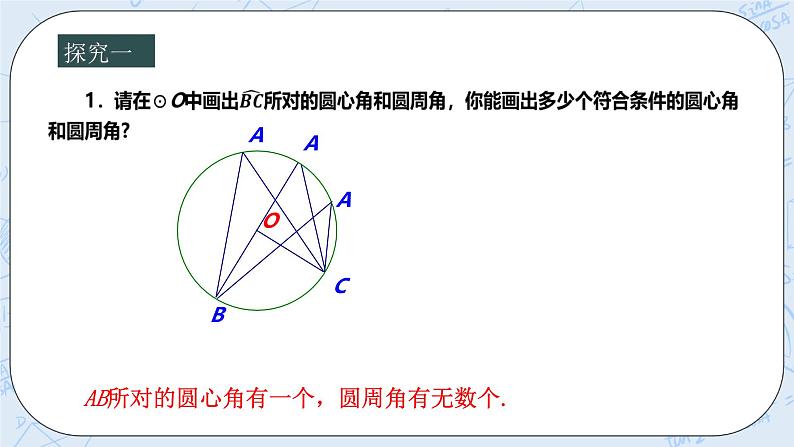
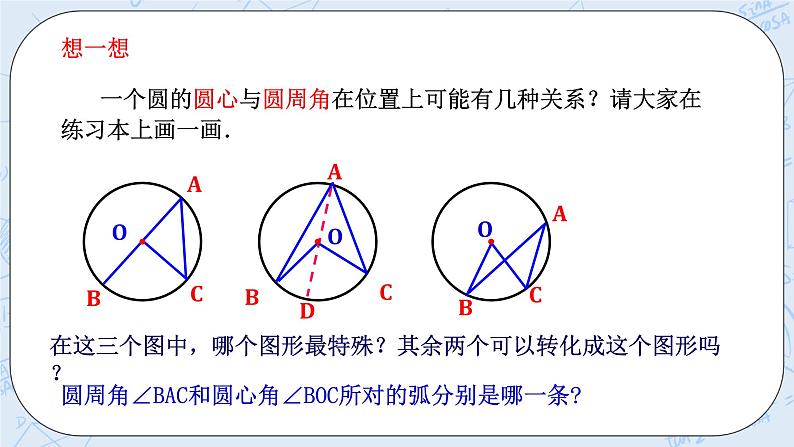
AB所对的圆心角有一个,圆周角有无数个. 探究1:如图,量出圆周角∠BAC与同弧上所对的圆心角∠BOC的度数,两者之间有什么关系? 探究2 当点A在弧BEC上移动的过程中,∠BAC与圆心O有几种不同的位置关系?画一画 探究3:量一量每次变化后∠BAC的度数,你发现了什么?给出你的猜想? 并证明 猜想:∠BAC=1/2∠BOC 一条弧所对的圆周角等于它所对的圆心角的一半. 证明猜想 已知:如图,∠BOC和∠BAC分别是弧BC所对的圆心角和圆周角 求证:∠BAC=∠BOC. 证明:分三种情况进行证明 圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半。 问题探究 1.如图所示,若AB是⊙O的直径,则半圆ADB所对的圆心角是哪一个角?角度是多少? 答:∠AOB,180°. 2. ∠C是多少度?为什么? 答:∠C=90°,一条弧所对的圆周角 等于它所对圆心角的一半.
3. 若已知∠C是直角,能否说明AB是⊙O的直径?为什么? 答:若已知∠C是直角,则∠AOB=180°,所以点A,O,B在一条直线上,AB是⊙O的直径.
二、提炼概念
归纳: 1.圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半。 2.圆周角定理的推论: 半圆(或直径)所对的圆周角是直角; 90°的圆周角所对的弦是直径.
| 思考 自议 圆周角必须具备的两个条件:①顶点在圆上;②角的两边都与圆相交,二者缺一不可.
|
学生思考进行分类证明,最后得出圆周角定理.
|
讲授新课 | 三、典例精讲 例1、如图 ,等腰三 角形ABC 的顶角∠BAC 为 50°,以 腰AB为直径作半圆,交BC为点D,交AC于点E,求弧BD,弧DE和弧AE的度数. 解: 连结BE,AD ∵ AB是圆的直径 ∴∠AEB=∠ADB=90°(直径所对的圆周角是直角) ∵∠BAC=50° ∴∠ABE=90°-∠BAC=90°-50°=40° 又∵△ABC是等腰三角形,
|
直径是构造直角的一个重要条件,一般是构造相关的弦,把直径所对的圆周角转化为90°的角,可以简单说成“有直径,造直角”.
| 增强学生观察和归纳总结的能力。
|
课堂检测 | 四、巩固训练 1.如图所示,已知圆心角∠BOC=78°,则圆周角∠BAC的度数是 ( ) A.156° B.78° C.39° D.12° 答案:A 2.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B处的读数分别为86°,30°,则∠ACB的大小为 ( ) A.15° B.28° C.29° D.34° 答案:B 3.如图所示,弦AB把圆周分成1∶5的两个部分,那么弦AB所对的圆周角的度数是______________.
【解析】 先求出的度数,再通过同弧所对的圆周角和圆心角的关系,求所对的圆周角的度数,分点在的劣弧和优弧上两种情形. 当点P在劣弧上时,可知∠P=150°, 当点P,在优弧上时,可知∠P=30° ∴弦AB所对的圆周角的度数为30°或150°. 4.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E. (1)求证:AB=AC; (2)若⊙O的半径为4,∠BAC=60°,求DE的长.
解:(1)连结AD. ∵AB是⊙O的直径, ∴∠ADB=90°.∵DC=BD,∴AB=AC. (2)∵∠BAC=60°,又由(1)知AB=AC, ∴△ABC是等边三角形. 在Rt△BAD中,∠BAD=30°,AB=8, ∴BD=4,即DC=4. 又∵DE⊥AC, ∴DE=2.
|
|
|
课堂小结 | 1、圆周角的定义: 顶点在圆上,两边都与圆相交的角. 2、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半. 3、圆周角定理的推论: 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
|
|
|
初中数学4.1 比例线段完美版ppt课件: 这是一份初中数学4.1 比例线段完美版ppt课件,文件包含浙教版数学九上412比例线段课件pptx、浙教版数学九上412比例线段教案doc、浙教版数学九上412比例线段学案doc等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学浙教版九年级上册3.5 圆周角评优课ppt课件: 这是一份初中数学浙教版九年级上册3.5 圆周角评优课ppt课件,文件包含浙教版数学九上352圆周角课件pptx、浙教版数学九上352圆周角学案doc、浙教版数学九上352圆周角教案doc等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
初中数学3.3 垂径定理精品ppt课件: 这是一份初中数学3.3 垂径定理精品ppt课件,文件包含浙教版数学九上332垂径定理课件pptx、浙教版数学九上332垂径定理教案doc、浙教版数学九上332垂径定理学案doc等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。













