初中数学人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线备课ppt课件

这是一份初中数学人教版七年级下册第五章 相交线与平行线5.2 平行线及其判定5.2.1 平行线备课ppt课件，共31页。PPT课件主要包含了平行线的定义，平行线的画法，实践应用等内容，欢迎下载使用。

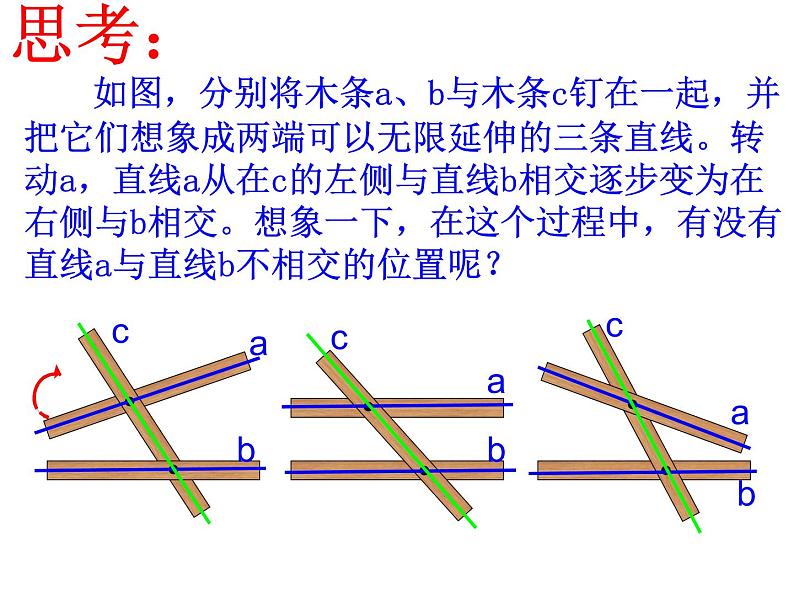
如图，分别将木条a、b与木条c钉在一起，并把它们想象成两端可以无限延伸的三条直线。转动a，直线a从在c的左侧与直线b相交逐步变为在右侧与b相交。想象一下，在这个过程中，有没有直线a与直线b不相交的位置呢？
在木条转动过程中，存在一个直线a与直线b不相交的位置，这时我们说直线a与b互相平行。
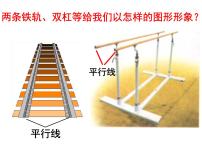
平行线在生活中是很常见的，你还 能举出其他一些例子吗？
在同一平面内，不相交的两条直线叫平行线．
平行线的定义包含三层意思： （1）“在同一平面内”是前提条件，（2）“不相交”就是说两条直线没有 交点，（3）平行线指的是“两条直线”而不 是两条射线或两条线段．
如何用几何语言描述平行呢？
2、平行线的表示方法：
平行用符号“∥”表示，如：直线AB与直线CD平行，记作：AB∥CD，读作“AB平行于CD”。
注意：平行线是相互的，使用平行符号“∥”时，可写成AB∥CD，也可以写成： CD∥AB。
如果用a、b表示这两条直线，那么直线a与直线b平行，记作：a∥b．也可以写成： b ∥ a 。
在同一平面内，两条直线有几种位置关系？动手画一画？
同一平面内两直线的位置关系：
结论：在同一平面内，两直线的位置 关系有平行与相交两种。
（1）你能在右图中的方格中画出 平行线吗？
方法：①利用方格纸中的直线画平行线。
②利用格点（长方形的对角线）画平行线。
（2）若改方格纸为白纸，你能利用以下哪些工具： ①直尺 ②三角板 ③量角器 画已知直线AB的平行线？能画多少条？
已知直线AB，画一条直线和已知直线AB平行
若将此处的直角改为锐角将会怎样？
“推平行线法”：
已知直线AB和直线外一点P，过点P画一条直线和已知直线AB平行。
一般地，经过直线外一点，有且只有一条直线与这条直线平行。
说明：人们在长期实践中总结出来的结论叫基本事实，也称为公理，它可以作为以后推理的依据．
平行线的性质(平行公理)
(1)经过点A画出直线n的平行线，能画几条？
(2)过点B画一条直线与直线n平行，它与(1)中所画的直线平行吗？
如果两条直线都和第三条直线平行，那么这两条直线也互相平行。
平行线的传递性 (平行公理的推论)：
几何语言表达式：∵a∥n m∥n（已知） ∴a∥m （平行线的传递性）
1、在同一个平面内， 的两条直线叫做平行线.则在同一个平面内两条直线的位置关系是 .
AB∥ CD，AD∥ BC。
如图，在⊿ ABC中，P是AC边上一点.过点P分别画AB，BC的平行线.
如图，中，P是AC边上一点.过点P分别画AB，BC的在⊿ ABC平行线.
∴PD、PE就是所要画的直线。
　１.同一平面内，三条直线的交点可以有　　　　　　　个．
　２.对于同一平面内的直线a、b、c，如果a∥b，c与a相交，那么c与b是什么位置关系?
3、完成下列推理，并在括号内注明理由。（1）如图1所示，因为AB // DE，BC // DE（已知）。所以A,B,C三点___________（ ）（2）如图2所示，因为AB // CD，CD // EF（已知），所以________ // _________( )
经过直线外一点,有且只有一条直线与这条直线平行
如果两条直线都和第三条直线平行，那么这两条直线也互相平行
　4.画∠AOB，在OB上取一点C，过点C画CD平行于OA，在OA上任取一点E，过点E画EF∥OB交CD于F，分别量得∠AOB、∠EFC，可得：___________；再测量∠AOB和∠OEF，可得__________________.
∠AOB＋∠OEF＝１８０°
本节课你的收获是什么？
(1) 平行线的定义；
(2)平行线的表示方法;
(3)两条直线在同一平面内的位置关系。
(6)平行线公理的推论。
平行线：在同一平面内，不相交的两条 直线叫做平行线。
平行线的画法：1、借助方格纸画；2、借助三角尺画。（一放、二靠、三推、四画）
m//n AB//CD
平行线的性质：（平行公理）
经过直线外一点，有且只有一条直线与这条直线平行；