初中数学湘教版七年级下册4.5 垂线教课内容ppt课件

这是一份初中数学湘教版七年级下册4.5 垂线教课内容ppt课件，文件包含45垂线课件ppt、45垂线教案DOCX等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。

1.知道垂线及其相关概念.2.理解垂线与平行线的关系,并能进行相关的推理论证.3.让学生学习初步的几何推理的方法,培养逻辑思维能力.
垂线的概念及垂线的有关性质.
活动1 旧知回顾
1.两直线平行, ；同位角相等, ；同旁内角互补, .2.直角等于 ,一个平角的度数等于两个直角的度数和.
活动1 自主探究1
阅读教材P96“观察”,观察直线AB与直线CD有什么位置关系？∠AOD有多少度？
解：AB与CD互相垂直,∠AOD＝90°.
活动2 合作探究1
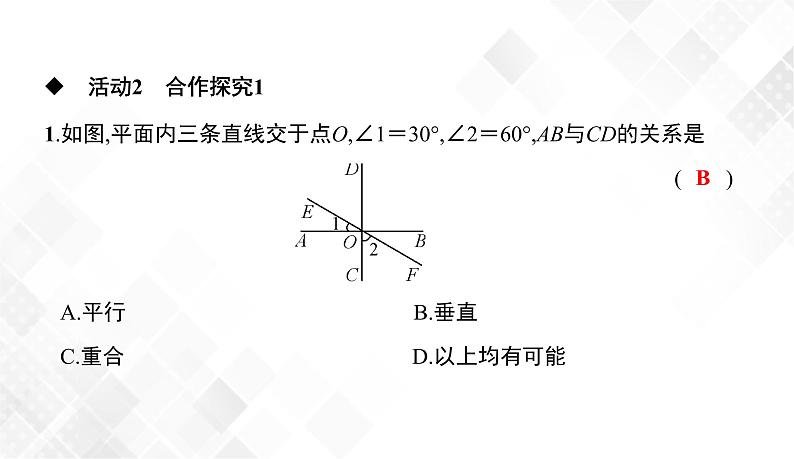
1.如图,平面内三条直线交于点O,∠1＝30°,∠2＝60°,AB与CD的关系是 (　　)
A.平行　　　　　 　B.垂直C.重合 D.以上均有可能
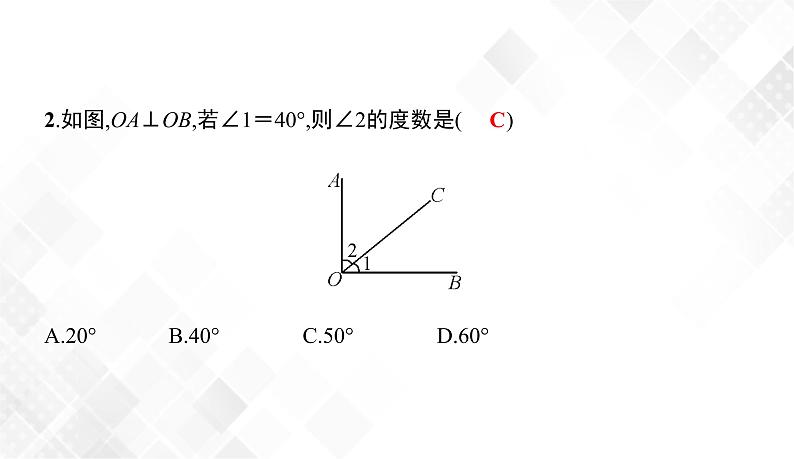
2.如图,OA⊥OB,若∠1＝40°,则∠2的度数是(　　)
A.20° B.40° C.50° D.60°
活动3 自主探究2
阅读教材P97“动脑筋”,下成下列内容.
下列说法正确的是(　　)A.在同一平面内,若a⊥b, b⊥c,则a ⊥cB.在同一平面内,若a∥b, b⊥c,则a ∥cC.若a∥b, b∥c,则a ⊥cD.若a∥b, b∥c,则a∥c
活动4 合作探究2
如图,DA⊥AB, CD⊥DA,∠B＝33°,求∠C.
解：∵DA⊥AB, CD⊥DA,∴AB∥CD,∴∠B＋∠C＝180°.又∠B＝33°,∴∠C＝147°.
活动5 自主探究3
例1 如图的简易屋架中，BD，AE，HF都垂直于CG，若∠1＝60º，求∠2的度数．
解 : 因为BD，AE都垂直于CG，所以BD//AE（在平面内，垂直于同一条直线的两条直线平行）
从而 ∠2＝∠1＝60º （两直线平行，同位角相等）
例2 如图，已知CD⊥AB，∠1＝∠2，求∠BFE的度数．
解：因为∠1＝∠2，所以EF//CD （同位角相等，两直线平行）．
又因为CD⊥AB，所以EF⊥AB，即∠BFE＝90º
阅读教材P97－98例1,例2,完成例2中的填空.∴DC∥EF( ).∴∠BEF＝∠BDC＝90°( ).
同位角相等,两直线平行
两直线平行,同位角相等
1.如图所示,GF⊥BC于点F, DE⊥AB于点E, AC⊥ AB,∠ADE＝∠CGF,那么AD与BC垂直吗？请说明理由.
解：AD⊥BC.理由：∵DE⊥AB, AC⊥AB,∴DE∥AC.∴∠ADE＝∠CAD.又∠ADE＝∠CGF,∴∠CAD＝∠CGF.∴AD∥GF.又GF⊥ BC,∴AD⊥BC.
2.如图,CD⊥AB于点D, EF⊥AB于点F,∠1＝∠2,请问DG∥BC吗？如果平行,请说明理由.
解：DG∥BC.理由如下：∵CD⊥AB, EF⊥AB,∴CD∥EF(在同一平常面内,垂直于同一条直线的两条直线平行).∴∠2＝∠3(两直线平行,同位角相等).又∵∠1＝∠2,∴∠1＝∠3(等量代换).∴DG∥BC(内错角相等,两直线平行).
活动6 合作探究3
如图，直线AB，CD相交于O，EO⊥CD, ∠BOE＝60º，求∠AOC的度数．
解:∵ EO⊥CD
又 ∠BOE+∠BOD＝∠EOD＝90°
∴ ∠BOD＝90°－∠BOE＝90°－60°＝30°
又 ∠BOD＝∠AOC
∴ ∠AOC＝30°
活动7 课堂小结
当两条直线相交所成的四个角中，有一个角是直角时，这两条直线互相垂直，其中一条直线叫另一条直线的垂线，它们的交点叫垂足.
在平面内垂直于同一条两条直线平行.
在平面内，如果一直线垂直于两平行线中的一条，那么这条直线必垂直于另一条.
1．作业布置对应课时练习．