






初中湘教版4.4 平行线的判定评课课件ppt
展开1.利用基本事实“同位角相等,两直线平行”推导判定平行线的另外两种方法,并能运用判定方法2、3进行简单的推理论证,解决相关的计算问题.2.让学生运用数形结合的数学思想方法,培养观察——分析和归纳——总结的能力.
会用“内错角相等,两直线平行”和“同旁内角互补,两直线平行”的判定方法.
活动1 旧知回顾
1.平行线的判定方法: .2.∠1,∠2是平行直线a、b被直线c所截形成的同位角,且∠1=60°,那么∠2= .
同位角相等,两直线平行
活动1 自主探究1
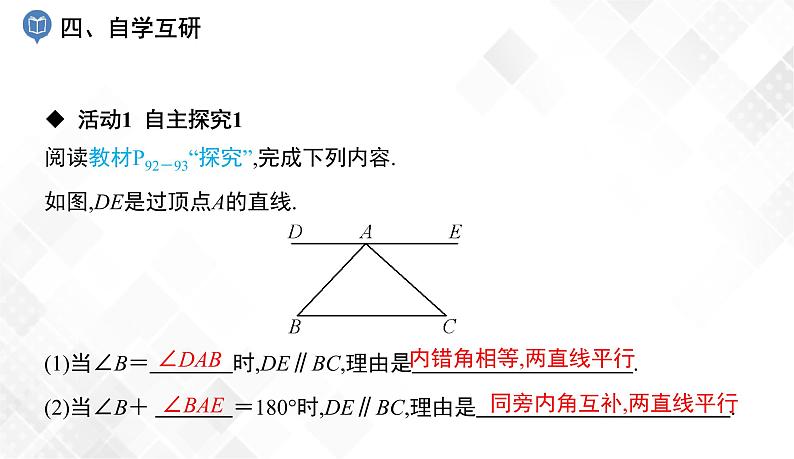
阅读教材P92-93“探究”,完成下列内容.如图,DE是过顶点A的直线.
(1)当∠B= 时,DE∥BC,理由是 .(2)当∠B+ =180°时,DE∥BC,理由是 .
内错角相等,两直线平行
同旁内角互补,两直线平行
活动2 合作探究1
如图,在括号内填上理由:
(1)因为∠1=∠2(已知),所以 ∥ ( );(2)因为∠3=∠2(已知),所以 ∥ ( );(3)因为∠4+∠2=180°(已知),所以 ∥ ( ).
归纳:平行线的判定2、31.两条直线被第三条直线所截,如果内错角相等,则两条直线平行.简单的说,内错角相等,两直线平行.2.两条直线被第三条直线所截,如果同旁内角互补,则两条直线平行.简单的说,同旁内角互补,两直线平行.
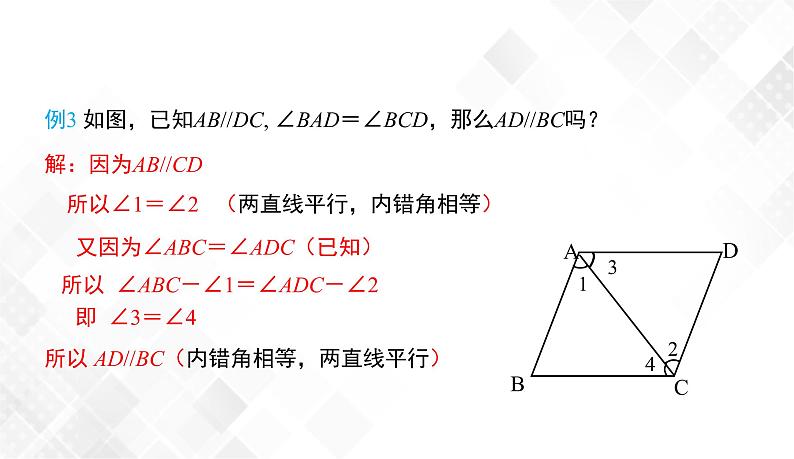
例3 如图,已知AB//DC, ∠BAD=∠BCD,那么AD//BC吗?
解:因为AB//CD 所以∠1=∠2 (两直线平行,内错角相等)
又因为∠ABC=∠ADC(已知)
所以 ∠ABC-∠1=∠ADC-∠2
所以 AD//BC(内错角相等,两直线平行)
活动3 自主探究2
阅读教材P93例4,理清推理过程,并完成下列内容.如图,在△ABC中,点D、E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥ BC,需要的条件是( )
A.∠1=∠2 B.∠1=∠DFEC.∠1=∠AFD D.∠2=∠AFD
活动4 合作探究2
1.如图,AD与BC相交于点O,∠B=∠C,试问∠A与∠D什么关系?为什么?
解:∠A=∠D.理由:∵∠B=∠C,∴AB∥CD,∴∠A=∠D.
2.如图,已知∠B+∠D=∠BED,试说明AB∥ CD.
证明:过E作EF∥AB,则∠BEF=∠B,∠BED=∠BEF+∠FED,∠BED=∠B+∠D,∴∠D=∠FED,∴EF∥CD.又EF∥AB,∴AB∥CD.
归纳:两直线平行,同位角(内错角)相等或同旁内角互补;反过来,同位角(内错角)相等或同旁内角互补,两直线平行.即平行线的性质和判定的结论与条件是互逆的.
1. 如图3-73,点A在直线l上,如果∠B=75°, ∠C=43°,则:
(1)当∠1= 时,直线l∥BC;(2)当∠2= 时,直线l∥BC;(3)若 l∥BC, ∠BAC=
2. 如图3-74,指出一个能推出AB∥CD的条件, 并说明理由。
答:如∠ACD=∠BAC. 或∠ADC+∠BAD = 180°等等.
活动6 课堂小结
1.同位角相等, 两直线平行.2.内错角相等, 两直线平行.3.同旁内角互补, 两直线平行.4.平行于同一直线的两直线平行.5.平行线的定义.
判定两条直线是否平行的方法有:
1.作业布置对应课时练习.
初中数学湘教版七年级下册4.4 平行线的判定课堂教学课件ppt: 这是一份初中数学湘教版七年级下册<a href="/sx/tb_c95253_t3/?tag_id=26" target="_blank">4.4 平行线的判定课堂教学课件ppt</a>,共23页。PPT课件主要包含了∠1∠3,AB∥CD,平行线的判定方法2,何言几语,∠1∠2,应用格式,BCD,解AB∥CD等内容,欢迎下载使用。
初中数学湘教版七年级下册4.4 平行线的判定多媒体教学ppt课件: 这是一份初中数学湘教版七年级下册4.4 平行线的判定多媒体教学ppt课件,文件包含44平行线的判定pptx、44平行线的判定练习doc、44平行线的判定docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
初中数学湘教版七年级下册第4章 相交线与平行线4.4 平行线的判定教案配套ppt课件: 这是一份初中数学湘教版七年级下册第4章 相交线与平行线4.4 平行线的判定教案配套ppt课件,文件包含44平行线的判定1课件ppt、44平行线的判定1教案DOCX等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。













