






初中数学湘教版九年级上册第1章 反比例函数1.3 反比例函数的应用教课ppt课件
展开1. 体会数学与现实生活的紧密联系,增强应用意识, 提高运用代数方法解决问题的能力.2. 能够通过分析实际问题中变量之间的关系,建立反 比例函数模型解决问题,进一步提高运用函数的图 象、性质的综合能力. (重点、难点)3. 能够根据实际问题确定自变量的取值范围.
对于一个矩形,当它面积一定时,长a是宽b的反比例函数,其函数解析式可以写为 (S > 0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数解析式.实例:函数解析式: .
三角形的面积 S 一定时,三角形底边长 y 是高 x的反比例函数
引例:某校科技小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p (Pa)将如何变化?如果人和木板对湿地地面的压力合计600N,那么(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
反比例函数在实际生活中的应用
由p= 得p=p是S的反比例函数,因为给定一个S的值,对应的就有唯一的一个p值和它对应,根据函数定义,则p是S的反比例函数.
(2)当木板面积为0.2m2时,压强是多少?
当S=0.2m2时,p= =3000(Pa) .答:当木板面积为0.2m2时压强是3000Pa.
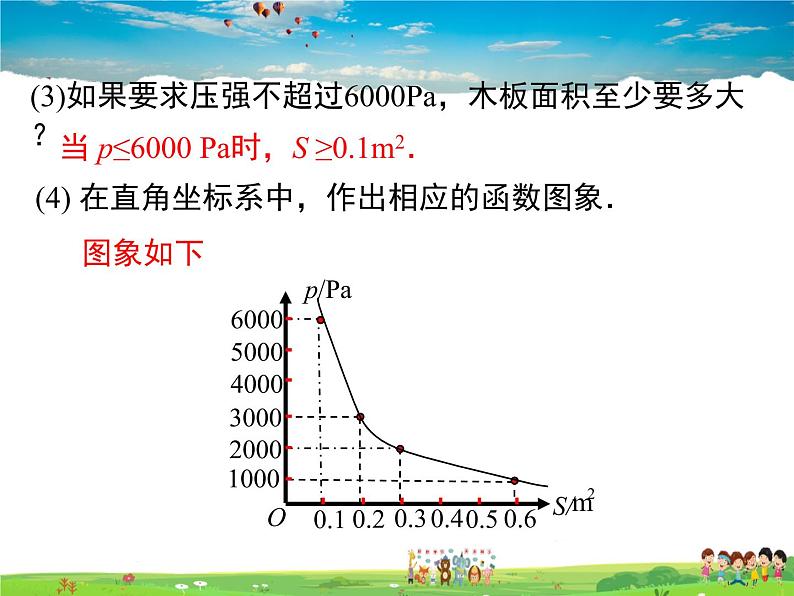
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
(4) 在直角坐标系中,作出相应的函数图象. 图象如下
当 p≤6000 Pa时,S ≥0.1m2.
例1 市煤气**学校要在地下修建一个容积为104 m3的圆柱形煤气储存室.(1) 储存室的底面积 S (单位:m2) 与其深度 d (单位:m) 有怎样的函数关系?
解:根据圆柱体的体积公式,得 Sd =104,
∴ S 关于d 的函数解析式为
(2) **学校决定把储存室的底面积 S 定为 500 m2,施工队 施工时应该向下掘进多深?
解得 d = 20.如果把储存室的底面积定为 500 m²,施工时应向地下掘进 20 m 深.
(3) 当施工队按 (2) 中的计划掘进到地下 15 m 时,公 司临时改变计划,把储存室的深度改为 15 m. 相 应地,储存室的底面积应改为多少 (结果保留小 数点后两位)?
解得 S≈666.67.
当储存室的深度为15 m 时,底面积应改为 666.67 m².
第 (2) 问和第 (3) 问与过去所学的解分式方程和求代数式的值的问题有何联系?
第 (2) 问实际上是已知函数 S 的值,求自变量 d 的取值,第 (3) 问则是与第 (2) 问相反.
1. 矩形面积为 6,它的长 y 与宽 x 之间的函数关系用 图象可表示为 ( )
2. 如图,某玻璃器皿制造**学校要制造一种容积为1升 (1升=1立方分米)的圆锥形漏斗. (1) 漏斗口的面积 S (单位:dm2)与漏斗的深 d (单位: dm) 有怎样的函数关系?
(2) 如果漏斗的深为10 cm,那么漏斗口 的面积为多少 dm2?
解:10cm=1dm,把 d =1 代入解析式,得 S =3. 所以漏斗口的面积为 3 dm2.
(3) 如果漏斗口的面积为 60 cm2,则漏斗的深为多少?
解:60 cm2 = 0.6 dm2,把 S =0.6 代入解析式,得 d =5. 所以漏斗的深为 5 dm.
例2 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.(1) 轮船到达目的地后开始卸货,平均卸货速度v (单位:吨/天)与卸货天数 t 之间有怎样的函数关系?
提示:根据平均装货速度×装货天数=货物的总量,可以求出轮船装载货物的总量;再根据平均卸货速度=货物的总量÷卸货天数,得到 v 关于 t 的函数解析式.
解:设轮船上的货物总量为 k 吨,根据已知条件得 k =30×8=240, 所以 v 关于 t 的函数解析式为
(2) 由于遇到紧急情况,要求船上的货物不超过 5天卸 载完毕,那么平均每天至少要卸载多少吨?
从结果可以看出,如果全部货物恰好用 5 天卸载完,则平均每天卸载 48 吨. 而观察求得的反比例函数的解析式可知,t 越小,v 越大. 这样若货物不超过 5 天卸载完,则平均每天至少要卸载 48 吨.
某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把 1200 立方米的生活垃圾运走.(1) 假如每天能运 x 立方米,所需时间为 y 天,写出 y 与 x 之间的函数关系式;
(2) 若每辆拖拉机一天能运 12 立方米,则 5 辆这样的 拖拉机要用多少天才能运完?
解:x =12×5=60,代入函数解析式得
答:若每辆拖拉机一天能运 12 立方米,则 5 辆这样的拖拉机要用 20 天才能运完.
(3) 在 (2) 的情况下,运了 8 天后,剩下的任务要在不 超过 6 天的时间内完成,那么至少需要增加多少 辆这样的拖拉机才能按时完成任务?
解:运了8天后剩余的垃圾有 1200-8×60=720 (立方米), 剩下的任务要在不超过6天的时间完成,则每天 至少运 720÷6=120 (立方米), 所以需要的拖拉机数量是:120÷12=10 (辆), 即至少需要增加拖拉机10-5=5 (辆).
例3 一司机驾驶汽车从甲地去乙地,他以 80千米/时 的平均速度用 6 小时达到乙地. (1) 甲、乙两地相距多少千米?
解:80×6=480 (千米)答:甲、乙两地相距 480 千米.
(2) 当他按原路匀速返回时,汽车的速度 v 与时间 t 有怎样的函数关系?
解:由题意得 vt=480,
例4 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为 1200 N 和 0.5 m.(1) 动力 F 与动力臂 l 有怎样的函数关系? 当动力臂为 1.5 m时,撬动石头至少需要多大的力?
解:根据“杠杆原理”,得 Fl =1200×0.5,
反比例函数在其他学科中的应用
(2) 若想使动力 F 不超过题 (1) 中所用力的一半,则 动力臂l至少要加长多少?
300-1.5 =1.5 (m).
在物理中,我们知道,在阻力和阻力臂一定的情况下,动力臂越长就越省力,你能用反比例函数的知识对其进行解释吗?
假定地球重量的近似值为 6×1025 牛顿 (即阻力),阿基米德有 500 牛顿的力量,阻力臂为 2000 千米,请你帮助阿基米德设计,该用多长动力臂的杠杆才能把地球撬动?
由已知得F×l=6×1025×2×106 =1.2×1032 米,
当 F =500时,l =2.4×1029 米,
解: 2000 千米 = 2×106 米,
故用2.4×1029 米动力臂的杠杆才能把地球撬动.
例5 一个用电器的电阻是可调节的,其范围为 110~220 Ω. 已知电压为 220 V,这个用电器的电路图如图所示.(1) 功率 P 与电阻 R 有怎样的函数关系?
解:根据电学知识, 当 U = 220 时,得
(2) 这个用电器功率的范围是多少?
解:根据反比例函数的性质可知,电阻越大,功率 越小. 把电阻的最小值 R = 110 代入求得的解析式, 得到功率的最大值 把电阻的最大值 R = 220 代入求得的解析式, 得到功率的最小值
因此用电器功率的范围为220~440 W.
1. 在公式 中,当电压 U 一定时,电流 I 与电 阻 R 之间的函数关系可用图象大致表示为 ( )
2. 在某一电路中,保持电压不变,电流 I (安培) 和电阻R (欧姆) 成反比例,当电阻 R=5 欧姆时,电流 I=2安培. (1) 求 I 与 R 之间的函数关系式; (2) 当电流 I=0.5 时,求电阻 R 的值.
解:(1) 设 ∵ 当电阻 R = 5 欧姆时,电流 I = 2 安培, ∴ U =10. ∴ I 与 R 之间的函数关系式为
1. 面积为 2 的直角三角形一直角边为x,另一直角边 长为 y,则 y 与 x 的变化规律用图象可大致表示为 ( )
2. (1) 体积为 20 cm3 的面团做成拉面,面条的总长度 y (单位:cm) 与面条粗细 (横截面积) S (单位:cm2)的函数关系为 .
(2) 某家面馆的师傅手艺精湛,他拉的面条粗 1 mm2,则面条的总长度是 cm.
3. A、B两城市相距720千米,一列火车从A城去B城. (1) 火车的速度 v (千米/时) 和行驶的时间 t (时) 之间的函数关系是________. (2) 若到达目的地后,按原路匀速返回,并要求 在 3 小时内回到 A 城,则返回的速度不能低 于____________.
4. 学校锅炉旁建有一个储煤库,开学时购进一批煤, 现在知道:按每天用煤 0.6 吨计算,一学期 (按150 天计算) 刚好用完. 若每天的耗煤量为 x 吨,那么 这批煤能维持 y 天. (1) 则 y 与 x 之间有怎样的函数关系?
解:煤的总量为:0.6×150=90 (吨),
(2) 画出函数的图象;
(3) 若每天节约 0.1 吨,则这批煤能维持多少天?
解:∵ 每天节约 0.1 吨煤, ∴ 每天的用煤量为 0.6-0.1=0.5 (吨), ∴ 这批煤能维持 180 天.
5. 王强家离工作单位的距离为3600 米,他每天骑自行 车上班时的速度为 v 米/分,所需时间为 t 分钟. (1) 速度 v 与时间 t 之间有怎样的函数关系?
(2) 若王强到单位用 15 分钟,那么他骑车的平均速 度是多少?
解:把 t =15代入函数的解析式,得:答:他骑车的平均速度是 240 米/分.
(3) 如果王强骑车的速度最快为 300 米/分,那他至少 需要几分钟到达单位?
解:把 v =300 代入函数解析式得: 解得:t =12.答:他至少需要 12 分钟到达单位.
6. 蓄电池的电压为定值.使用此电源时,电流 I (A) 是电阻 R (Ω) 的反比例函数,其图象如图所示. (1) 求这个反比例函数的表达式;
解:设 ,把 M (4,9) 代入得 k =4×9=36. ∴ 这个反比例函数的 表达式为 .
(2) 当 R =10Ω 时,电流能是 4 A 吗?为什么?
解:当 R=10Ω 时,I = 3.6 ≠ 4, ∴电流不可能是4A.
7. 某汽车的功率 P 为一定值,汽车行驶时的速度 v (m/s) 与它所受的牵引力F (N)之间的函数关系如 下图所示: (1) 这辆汽车的功率是多少?请写出这一函数的表 达式;
(3) 如果限定汽车的速度不超过 30 m/s,则 F 在什 么范围内?
(2) 当它所受牵引力为1200牛时,汽车的速度为多 少 km/h?
解:把 F = 1200 N 代入求得的解析式得 v = 50, ∴汽车的速度是3600×50÷1000 = 180 km/m.
答案:F ≥ 2000 N.
8. 在某村河治理工程施工过程中,某工程队接受一项 开挖水渠的工程,所需天数 y (天) 与每天完成的工 程量 x (m/天) 的函数关系图象如图所示. (1) 请根据题意,求 y 与 x 之间的函数表达式;
(2) 若该工程队有 2 台挖掘机,每台挖掘机每天能够 开挖水渠 15 m,问该工程队需用多少天才能完 成此项任务?
解:由图象可知共需开挖水渠 24×50=1200 (m); 2 台挖掘机需要 1200÷(2×15)=40 (天).
(3) 如果为了防汛工作的紧急需要,必须在一个月内 (按 30 天计算)完成任务,那么每天至少要完成多 少 m?
解:1200÷30=40 (m), 故每天至少要完成40 m.
湘教版九年级上册1.3 反比例函数的应用优秀课件ppt: 这是一份湘教版九年级上册1.3 反比例函数的应用优秀课件ppt,文件包含13反比例函数的应用-课件pptx、13反比例函数的应用-试卷doc、13反比例函数的应用-教学设计doc等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
数学九年级上册第1章 反比例函数1.3 反比例函数的应用完整版课件ppt: 这是一份数学九年级上册第1章 反比例函数1.3 反比例函数的应用完整版课件ppt,文件包含湘教版数学九上13《反比例函数的应用》课件pptx、费曼谈数学与物理的关系_mp4等2份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
数学九年级上册1.3 反比例函数的应用优秀教学ppt课件: 这是一份数学九年级上册1.3 反比例函数的应用优秀教学ppt课件,文件包含湘教版数学九年级上册13反比例函数的应用pptx、13反比例函数的应用doc、费曼谈数学与物理的关系mp4等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。













