初中数学人教版八年级上册11.1.2 三角形的高、中线与角平分线教学课件ppt

这是一份初中数学人教版八年级上册11.1.2 三角形的高、中线与角平分线教学课件ppt，共29页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，回顾旧知，垂线的定义，线段中点的定义，角平分线的定义，知识点等内容，欢迎下载使用。

三角形的高三角形的中线 三角形的角平分线
当两条直线相交所成的四个角巾，有一个角是直角时，就说这两条直线互相垂直， 其中一条直线叫做另一条直线的垂线.
把一条线段分成两条相等的线段的点.
一条射线把一个角分成两个相等的角，这条射线叫做这个角的平分线.
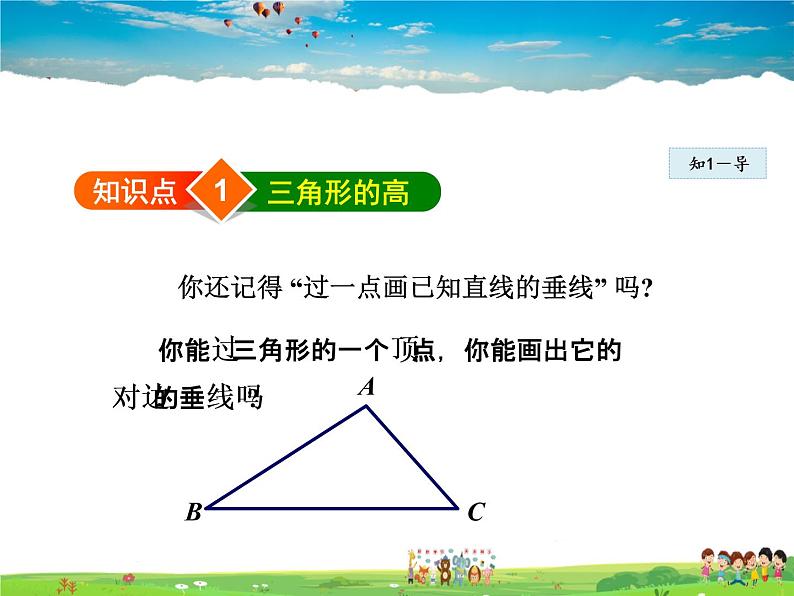
你能过三角形的一个顶点，你能画出它的对边的垂线吗?
你还记得 “过一点画已知直线的垂线” 吗?
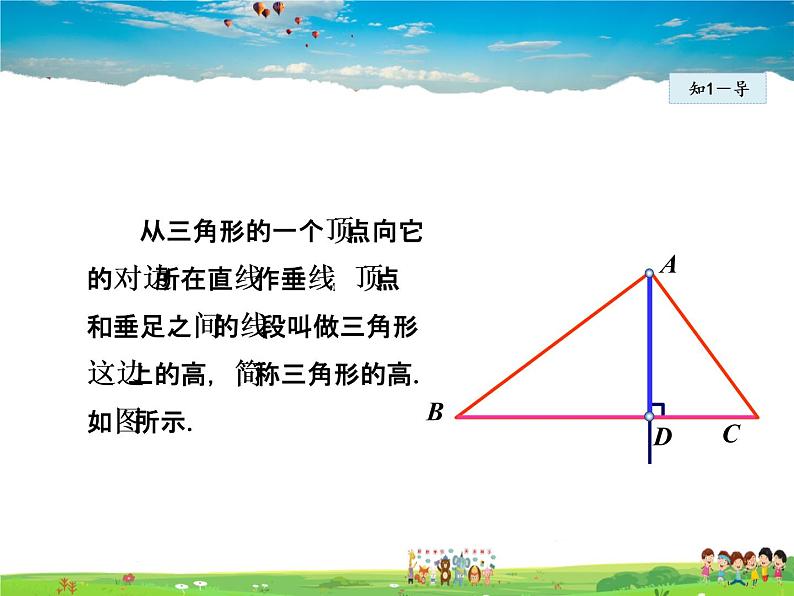
从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形这边上的高，简称三角形的高.如图所示.
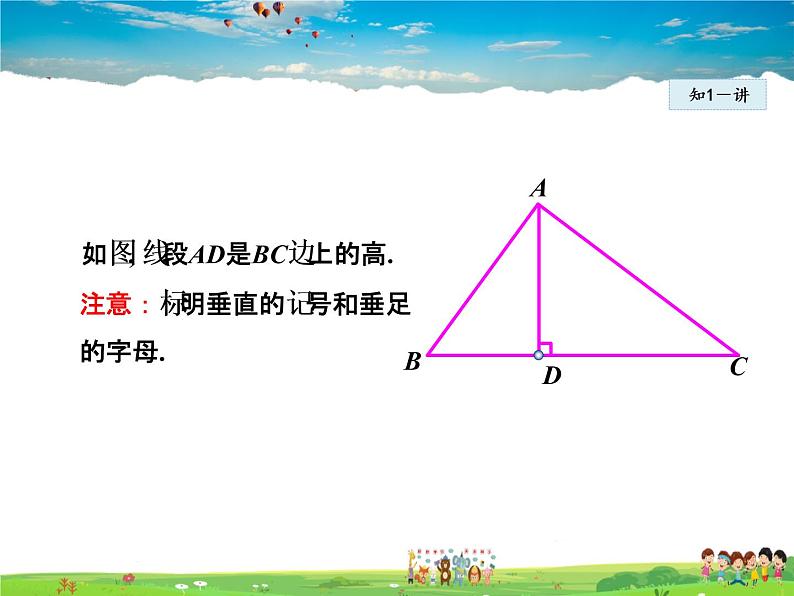
如图, 线段AD是BC边上的高.
注意：标明垂直的记号和垂足的字母.
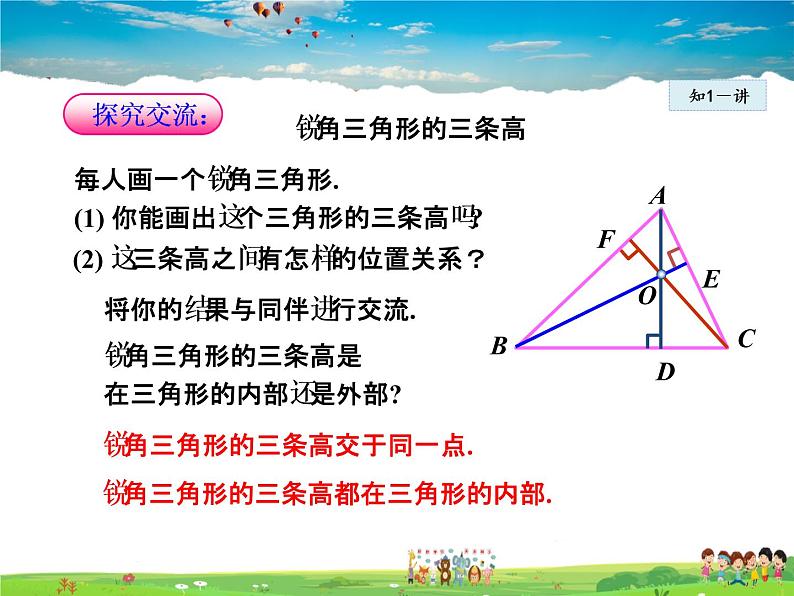
每人画一个锐角三角形.(1) 你能画出这个三角形的三条高吗?
(2) 这三条高之间有怎样的位置关系？
将你的结果与同伴进行交流.
锐角三角形的三条高是在三角形的内部还是外部?
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
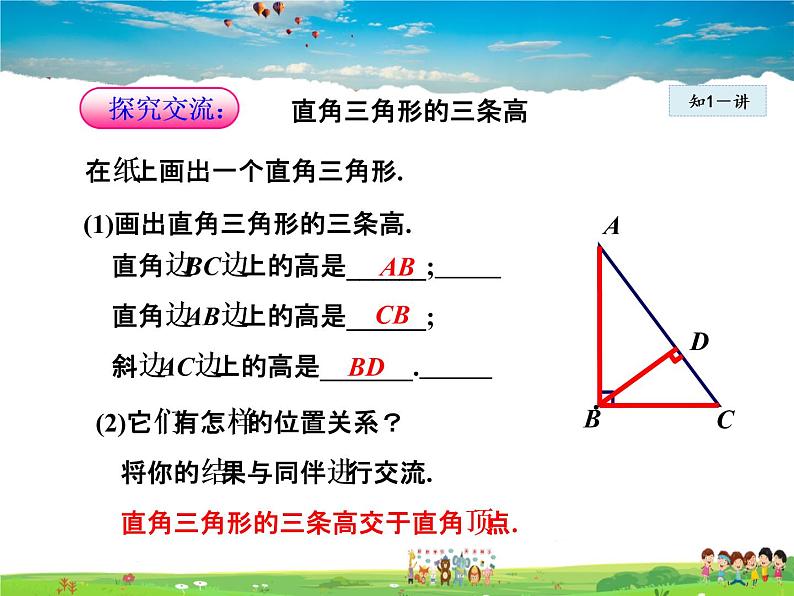
在纸上画出一个直角三角形.
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
直角边AB边上的高是______;
(2)它们有怎样的位置关系？
斜边AC边上的高是_______.
直角三角形的三条高交于直角顶点.
(1) 钝角三角形的三条高交于 一点吗？
(2)它们所在的直线交于一点吗？
钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
叫做三角形这边上的高.
从三角形的一个顶点向它的对边所在直线作垂线，
三角形的三条高的特性：
三条高所在直线的交点的位置
如图，(1) (2)和(3)中的三个∠B有什么不同？这三条△ABC的边BC上的高AD在各自三角形的什么位置？你能说出其中的规律吗？
(1)中的∠B是锐角，高AD在△ABC内部．(2)中的∠B是直角，高AD与边AB重合．(3)中的∠B是钝角，高AD的垂足在CB的延长线上， 即高AD在△ABC的外部． 当∠C是锐角时，如果∠B是锐角，高AD在△ABC 的内部；如果∠B是直角，高AD与边AB重合；如 果∠B是钝角，高AD的垂足在CB的延长线上，即 高AD在△ABC的外部．
在直角三角形中，有两条高是它的________，另一条高在这个三角形的________．锐角三角形的三条高的交点在______________，直角三角形的三条高的交点在_______________________，钝角三角形的三条高所在直线的交点在_________________．
如图 (1)，连接△ABC的顶点A和 它所对的边BC的中点D，所得线段AD叫做 △ABC的边BC上的中线.
用同样方法， 你能画出△ABC 的另两条边上的中 线吗？
在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形这边上的中线.
如图 (2),三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
取一块质地均匀的 三角形木板，顶住三条 中线的交点，木板会保 持平衡，这个平衡点就 是这块三角形木板的 重心.
在△ABC中，AB＝AC，AC边上的中线BD把△ABC的周长分为12 cm和15 cm两部分，求△ABC的各边长．　
因为中线BD将△ABC的周长分成两部分：(BC＋CD)和(AD＋AB)，无法确定谁为12 cm，谁为15 cm，故应分类讨论；另外题中涉及线段较多，因此可建立方程的模型，利用设未知数来求解．
设AB＝x cm，则AD＝CD＝ x cm.(1)如图①，若AB＋AD＝12 cm，则x＋ x＝12.解得x＝8，即AB＝AC＝8 cm，则CD＝4 cm.故BC＝15－4＝11(cm)．此时AB＋AC＞BC，三角形存在，所以三边长分别为8 cm，8 cm，11 cm.(2)如图②，若AB＋AD＝15 cm，则x＋ x＝15.解得x＝10，即AB＝AC＝10 cm，则CD＝5 cm.故BC＝12－5＝7(cm)．显然此时三角形存在，所以三边长分别为10 cm，10 cm，7 cm.综上所述，△ABC的三边长分别为8 cm，8 cm，11 cm或10 cm，10 cm，7 cm.
填空： 如图(1)，AD，BE，CF是△ABC的三条中线，则AB= 2 __________, BD=_______, AE= ________.
三角形一边上的中线把原三角形一定分成两个(　　)A．形状相同的三角形 　B．面积相等的三角形C．直角三角形 　 D．周长相等的三角形
如图，已知BD是△ABC的中线，AB＝5，BC＝3，△ABD和△BCD的周长的差是(　　)A．2　　　B．3　　　C．6　　　D．不能确定
如果现在你手上有一张画着一个三角形的薄纸，你能想几种办法画出它的一个内角的平分线？
叫做三角形的角平分线.
因为AD是△ABC的角平分线，
任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?
一个内角的角平分线与它的对边相交，
这个角的顶点与交点之间的线段,
三角形的三条角平分线相交于一点,交点在三角形的内部.
因为BE是△ABC的角平分线，
所以______=________= _______.
所以∠ACB=2_______ =2__________.
因为CF是△ABC的角平分线，
1.三角形的角平分线与角的平分线的区别是： 三角形的角平分线是线段，而角的平分线是一条射线； 它们的联系是都是平分角。
2.三角形的角平分线判别的“两种方法” (1)看该线段是否分三角形的内角为相等的两部分. (2)看线段的两个端点，其中一个端点是三角形的顶 点，另一个端点要落在对边上.
如下页图（2)，AD, BE, CF是△ ABC的三条角平分线，则∠1=______, ∠3= _______, ∠ACB= 2_______.
今天我们学了什么呢？1.三角形的高、中线、角平分线等有关概念及它们 的画法.2.三角形的高、中线、角平分线几何表达及简单应 用.