人教A版 (2019)必修 第一册4.2 指数函数图文ppt课件

这是一份人教A版 (2019)必修 第一册4.2 指数函数图文ppt课件，共22页。PPT课件主要包含了情景引入，新知导学，知识点拨，〔跟踪练习1〕，『规律方法』，〔跟踪练习2〕，〔跟踪练习3〕等内容，欢迎下载使用。

2010年11月1日，全国人口普查全面展开，而2000年我国约有13亿人口．我国政府现在实行计划生育政策，人口年增长率较低．若按年增长率1%计算，到2010年底，我国人口将增加多少？到2020年底，我国人口总数将达到多少？如果我们放开计划生育政策，年增长率是2%，甚至是5%，那么结果将会是怎样的呢？会带来灾难性后果吗？
1．指数函数的图象和性质指数函数的图象和性质如下表所示：
(1)a>1是“一撇”，0命题方向1　⇨指数函数的概念
典例1 (1)下列以x为自变量的函数中，是指数函数的是(　　)A．y＝(－4)x　　　　B．y＝πxC．y＝－4xD．y＝ax＋2(a>0，a≠1)(2)若y＝(a2－3a＋3)ax是指数函数，则有(　　)A．a＝1或2B．a＝1C．a＝2D．a>0且a≠1
[解析]　(1)函数y＝(－4)x的底数－4<0，故A中函数不是指数函数；函数y＝πx的系数为1，底数π>1，故B中函数是指数函数；函数y＝－4x的系数为－1，故C中函数不是指数函数；函数y＝ax＋2＝a2·ax的系数为a2，故D中函数不是指数函数，故选B．
(2)由题意，得 解得a＝2，故选C．
若函数y＝(m－2)ax＋3－2n(a>0，且a≠1)是指数函数，则k＝____，b＝____．
命题方向2　⇨指数函数的图象
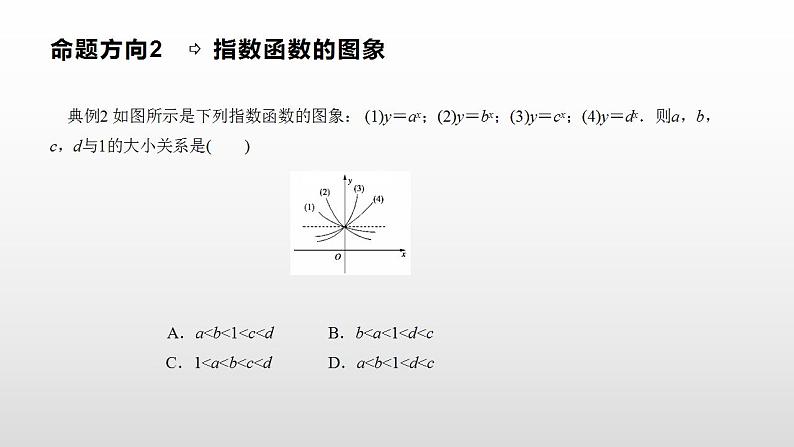
典例2 如图所示是下列指数函数的图象： (1)y＝ax；(2)y＝bx；(3)y＝cx；(4)y＝dx．则a，b，c，d与1的大小关系是(　　)
A．a[思路分析]　根据指数函数的底数与图象间的关系来进行判断．[解析]　可先分为两类，(3)(4)的底数一定大于1，(1)(2)的底数一定小于1，然后再由(3)(4)比较，c，d的大小，由(1)(2)比较a，b的大小．当指数函数的底数大于1时，图象上升，且当底数越大，图象向上越靠近y轴；当底数大于0小于1时，图象下降，且当底数越小，图象向下越靠近x轴，故选B．
指数函数图象的变化规律指数函数的图象随底数变化的规律可归纳为：在第一象限内， 图象自下而上对应的底数依次增大．
(2)若函数y＝ax＋(b－1)(a＞0，且a≠1)的图象不经过第二象限，则有(　D　)A．a＞1且b＜1 B．0＜a＜1且b≤1C．0＜a＜1且b＞0 D．a＞1且b≤0
指数函数中忽视对底数的分类讨论致误
典例3 函数f(x)＝ax(a＞0，且a≠1)在[0，1]上的最大值与最小值的差为 ，则a＝____________．
已知a＞0，且a≠1，若函数f(x)＝2ax－4在区间[－1，2]上的最大值为10，则a＝____．
转化与化归思想的应用 　
指数型函数的定义域、值域、图象与性质的讨论都可以化归为基本函数y＝ax(a>0且a≠1)的相关知识来解决．
1．指数型函数图象过定点问题
典例4 函数f(x)＝ax－1＋1(a>0且a≠1)过定点A，则A点的坐标为____．
[解析]　原函数f(x)＝ax－1＋1可变形为y－1＝ax－1，将y－1看作x－1的函数．令x－1＝0则y－1＝1即x＝1，y＝2，∴函数f(x)＝ax－1＋1恒过定点A(1，2)．
指数型函数过定点的求法求指数型函数图象所过的定点，只要令指数为0，求出对应的x与y的值，即为函数图象所过的定点．
2．指数型函数的定义域与值域
典例5 求下列函数的定义域与值域：
[思路分析]　(1)题中x－4满足什么条件时，函数有意义？y的值不可能取得什么？(2)题中式子的指数中含有根式，若要有意义，需满足什么条件？