

人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直第1课时课后复习题
展开8.6.3 平面与平面垂直
第1课时 平面与平面垂直的判定
(用时45分钟)
【选题明细表】
知识点、方法 | 题号 |
判定定理的理解及应用 | 1,3,6,7 |
二面角 | 2,4,9 |
综合应用 | 5,8,10,11,12 |
基础巩固
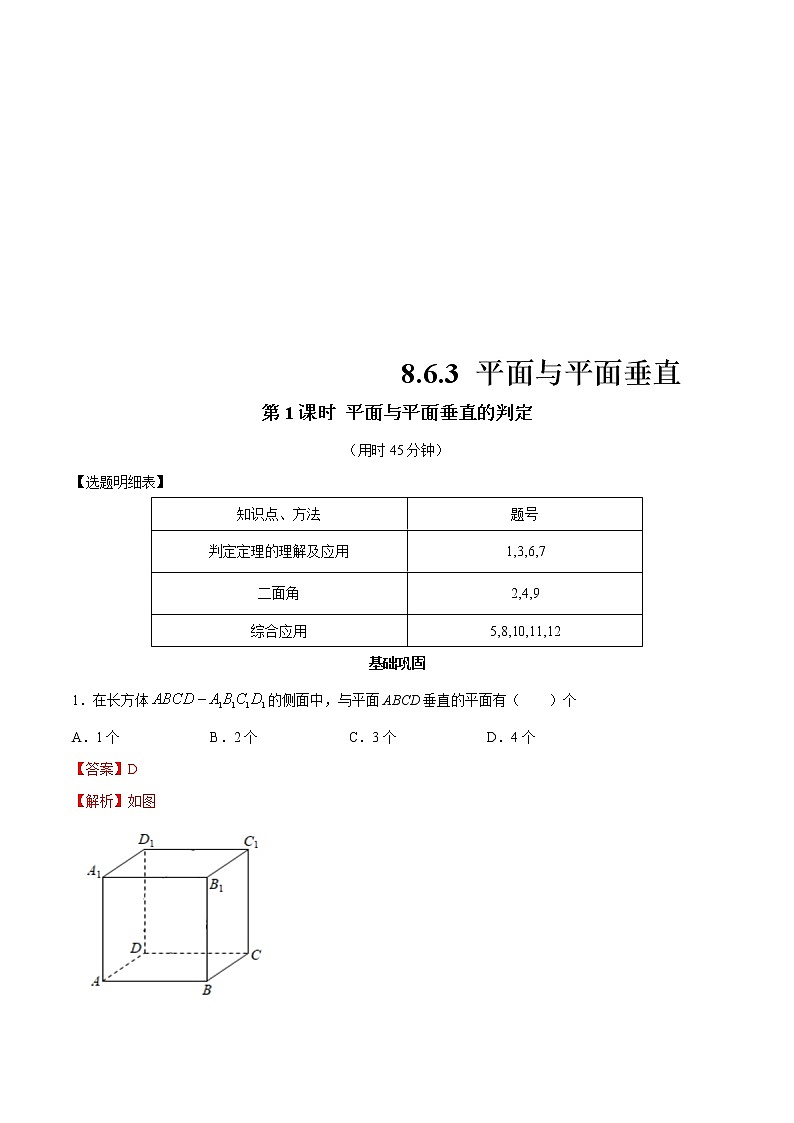
1.在长方体的侧面中,与平面ABCD垂直的平面有( )个
A.1个 B.2个 C.3个 D.4个
【答案】D
【解析】如图
在长方体中,侧棱与底面都是垂直的,所以侧面与底面ABCD垂直.
平面、平面、平面、平面均与平面ABCD垂直.
故选:D
2.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角的关系是( )
A.相等 B.互补 C.相等或互补 D.不确定
【答案】D
【解析】如图所示,在正方体中,二面角与二面角的两个半平面分别对应垂直,但是这两个二面角既不相等,也不互补,
所以这两个二面角不一定相等或互补.
例如:开门的过程中,门所在平面及门轴所在墙面分别垂直于地面与另一墙面,但门所在平面与门轴所在墙面所成二面角的大小不定,而另一二面角却是,所以这两个二面角不一定相等或互补.
3.垂直于正方形所在平面,连接,,,,,则下列垂直关系正确的个数是( )
①面面②面面
③面面④面面
A.1 B.2 C.3 D.4
【答案】B
【解析】证明:对于①,因为底面为正方形
所以
由题意可知平面
所以,
而
所以平面
又因为平面
所以平面平面,所以①正确;
对于②,因为
故由①可得平面,
而平面
所以平面平面,所以②正确
③④错误,不垂直.
综上可知,正确的为①②
故选:B
4.从空间一点P向二面角α-l-β的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角α-l-β的平面角的大小是( )
A.60° B.120°
C.60°或120° D.不确定
【答案】C
【解析】∠EPF=60°就是两个平面α和β的法向量的夹角,
它与二面角的平面角相等或互补,
故二面角的平面角的大小为60°或120°.
故选:C.
5.如图所示,在直角梯形BCEF中,∠CBF=∠BCE=90°,A,D分别是BF,CE上的点,AD∥BC,且AB=DE=2BC=2AF(如图1),将四边形ADEF沿AD折起,连结BE、BF、CE(如图2).在折起的过程中,下列说法中正确的个数( )
①AC∥平面BEF;
②B、C、E、F四点可能共面;
③若EF⊥CF,则平面ADEF⊥平面ABCD;
④平面BCE与平面BEF可能垂直
A.0 B.1 C.2 D.3
【答案】C
【解析】
对①,在图②中,连接交于点,取中点,连接MO,易证AOMF为平行四边形,即AC//FM,所以AC//平面BEF,故①正确;
对②,如果B、C、E、F四点共面,则由BC//平面ADEF,可得BC//EF,又AD//BC,所以AD//EF,这样四边形ADEF为平行四边形,与已知矛盾,故②不正确;
对③,在梯形ADEF中,由平面几何知识易得EFFD,又EFCF,∴EF平面CDF,
即有CDEF,∴CD平面ADEF,则平面ADEF平面ABCD,故③正确;
对④,在图②中,延长AF至G,使得AF=FG,连接BG,EG,易得平面BCE平面ABF,BCEG四点共面.过F作FNBG于N,则FN平面BCE,若平面BCE平面BEF,
则过F作直线与平面BCE垂直,其垂足在BE上,矛盾,故④错误.
故选:C.
6.设α,β是空间内两个不同的平面,m,n是平面α及β外的两条不同直线.从“①m⊥n;②α⊥β;③n⊥β;④m⊥α”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题:________(用序号表示).
【答案】①③④⇒②
【解析】将①③④作为条件,
因为所以 或,
又因为 ,所以
故①③④⇒②;
7.如图,AB为圆O的直径,点C在圆周上异于点A,,直线PA垂直于圆O所在的平面,点M是线段PB的中点有以下四个命题:
①∥平面;
②∥平面;
③平面;
④平面平面.
其中正确的命题的序号是______.
【答案】①④
【解析】对①,因为为的中点,故为三角形的中位线,故∥平面.
故①正确.
对②,因为平面,故②错误.
对③,因为,故不会垂直于,故不垂直于平面.故③错误
对④, 因为,面,故.又.
故平面,又平面,故平面平面.故④正确.
故答案为①④
8.如图所示,四棱锥的底面是边长为1的菱形,,
E是CD的中点,PA底面ABCD,.
(I)证明:平面PBE平面PAB;
(II)求二面角A—BE—P和的大小.
【答案】(I)同解析(II)二面角的大小为
【解析】(I)如图所示, 连结由是菱形且知,
△BCD是等边三角形. 因为E是CD的中点,所以
又所以
又因为PA平面ABCD,平面ABCD,
所以而因此平面PAB.
又平面PBE,所以平面PBE平面PAB.
(II)由(I)知,平面PAB,平面PAB, 所以
又所以是二面角的平面角.
在Rt△PAB中,.
故二面角的大小为
能力提升
9.在四面体中,已知棱的长为,其余各棱长都为1,则二面角的平面角的余弦值为( )
A. B. C. D.
【答案】C
【解析】
由已知可得AD⊥DC
又由其余各棱长都为1得正三角形BCD,取CD得中点E,连BE,则BE⊥CD
在平面ADC中,过E作AD的平行线交AC于点F,则∠BEF为二面角A﹣CD﹣B的平面角
∵EF=(三角形ACD的中位线),BE=(正三角形BCD的高),BF=(等腰RT三角形ABC,F是斜边中点)
∴cos∠BEF=
故选C.
10.如图所示,正方形的边长为,已知,将△ABE沿边折起,折起后点在平面上的射影为点,则翻折后的几何体中有如下描述:①与所成角的正切值为;②AB//CE;③;④平面平面,其中正确的命题序号为___________.
【答案】③④
【解析】
作出折叠后的几何体直观图如图所示:
∵AB=a,BE=a,∴AE=a.
∴.
∵BC∥DE,∴∠ABC是异面直线AB,DE所成的角,
在Rt△ABC中, ,故①不正确;
连结BD,CE,则CE⊥BD,
又AD⊥平面BCDE,CE⊂平面BCDE,
∴CE⊥AD,又BD∩AD=D,BD⊂平面ABD,AD⊂平面ABD,
∴CE⊥平面ABD,又AB⊂平面ABD,
∴CE⊥AB.故②错误.
三棱锥B−ACE的体积.
故③正确.
∵AD⊥平面BCDE,BC⊂平面BCDE,
∴BC⊥AD,又BC⊥CD,
∴BC⊥平面ACD,∵BC⊂平面ABC,
∴平面ABC⊥平面ACD.
故答案为③④.
11.如图,在四棱锥中,底面是边长为的正方形,侧棱,求证:
(1)平面;
(2)平面平面;
(3)二面角的平面角的大小.
【答案】(1)见解析;(2)见解析;(3)
【解析】(1),.
.
同理可证.
平面.
(2)由(1)知平面,平面,.
∵四边形是正方形,.
又,平面.
又平面,∴平面平面.
(3)由(1)知平面,平面,.
又,平面.
平面,.
为二面角的平面角.
在中,.
∴二面角的平面角的大小为45°.
素养达成
12.如图,矩形所在平面与半圆弧CD所在平面垂直,是CD上异于,的点.
(1)证明:平面平面;
(2)在线段上是否存在点,使得平面?说明理由.
【答案】(1)证明见解析.(2)存在,理由见解析.
【解析】(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM平面AMD,故平面AMD⊥平面BMC.
(2)当P为AM的中点时,MC∥平面PBD.
证明如下:连结AC交BD于O.因为ABCD为矩形,所以O为AC中点.
连结OP,因为P为AM 中点,所以MC∥OP.
MC平面PBD,OP平面PBD,所以MC∥平面PBD.
人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直第1课时课时练习: 这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直第1课时课时练习,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直第1课时同步练习题: 这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直第1课时同步练习题
高中数学8.6 空间直线、平面的垂直测试题: 这是一份高中数学8.6 空间直线、平面的垂直测试题,共26页。试卷主要包含了下列命题正确的是等内容,欢迎下载使用。













