北师大版七年级下册3 探索三角形全等的条件教案

这是一份北师大版七年级下册3 探索三角形全等的条件教案，共4页。
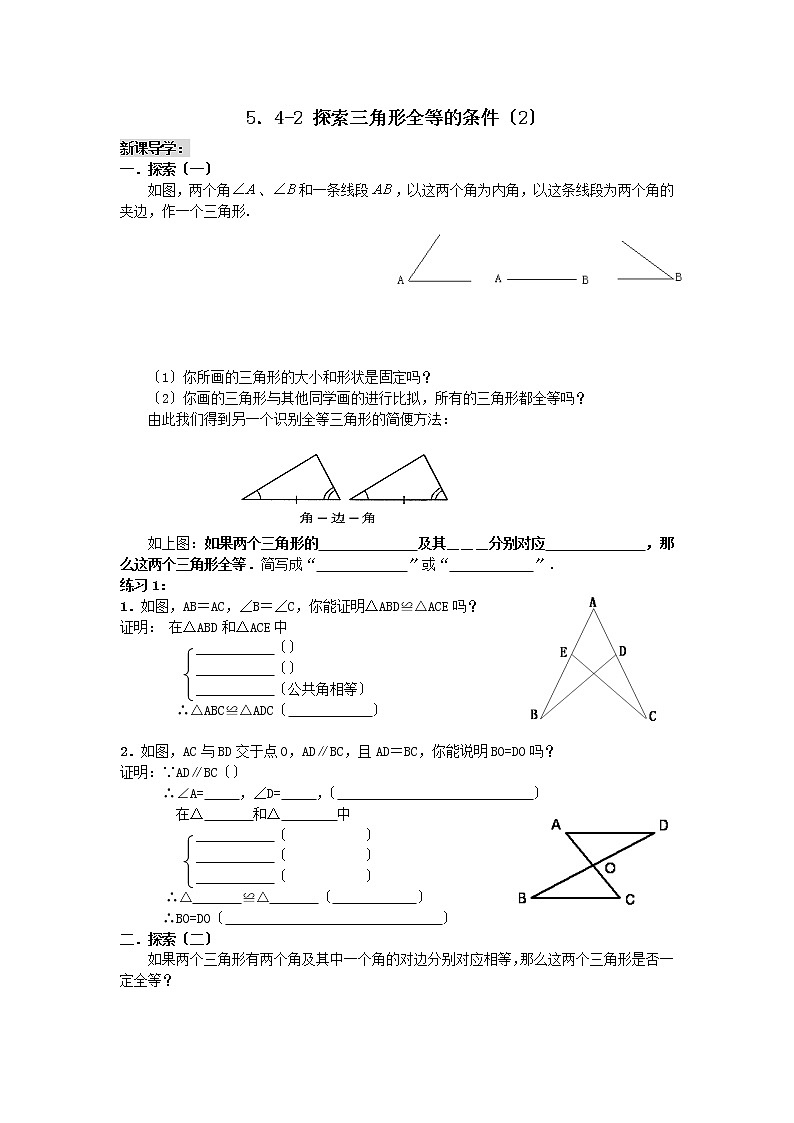
一．探索〔一〕
如图，两个角、和一条线段，以这两个角为内角，以这条线段为两个角的夹边，作一个三角形.
〔1〕你所画的三角形的大小和形状是固定吗？
〔2〕你画的三角形与其他同学画的进行比拟，所有的三角形都全等吗？
由此我们得到另一个识别全等三角形的简便方法：

如上图：如果两个三角形的 及其＿＿＿分别对应 ，那么这两个三角形全等．简写成“ 〞或“ 〞．
练习1：
1．如图，AB＝AC，∠B＝∠C，你能证明△ABD≌△ACE吗？
证明： 在△ABD和△ACE中
〔〕
〔〕
〔公共角相等〕
∴△ABC≌△ADC〔 〕
2．如图，AC与BD交于点O，AD∥BC，且AD＝BC，你能说明BO=DO吗？
证明：∵AD∥BC〔〕
∴∠A= ，∠D= ，〔 〕
在△ 和△ 中
〔 〕
〔 〕
〔 〕
∴△ ≌△ 〔 〕
∴BO=DO〔 〕
二．探索〔二〕
如果两个三角形有两个角及其中一个角的对边分别对应相等，那么这两个三角形是否一
定全等？
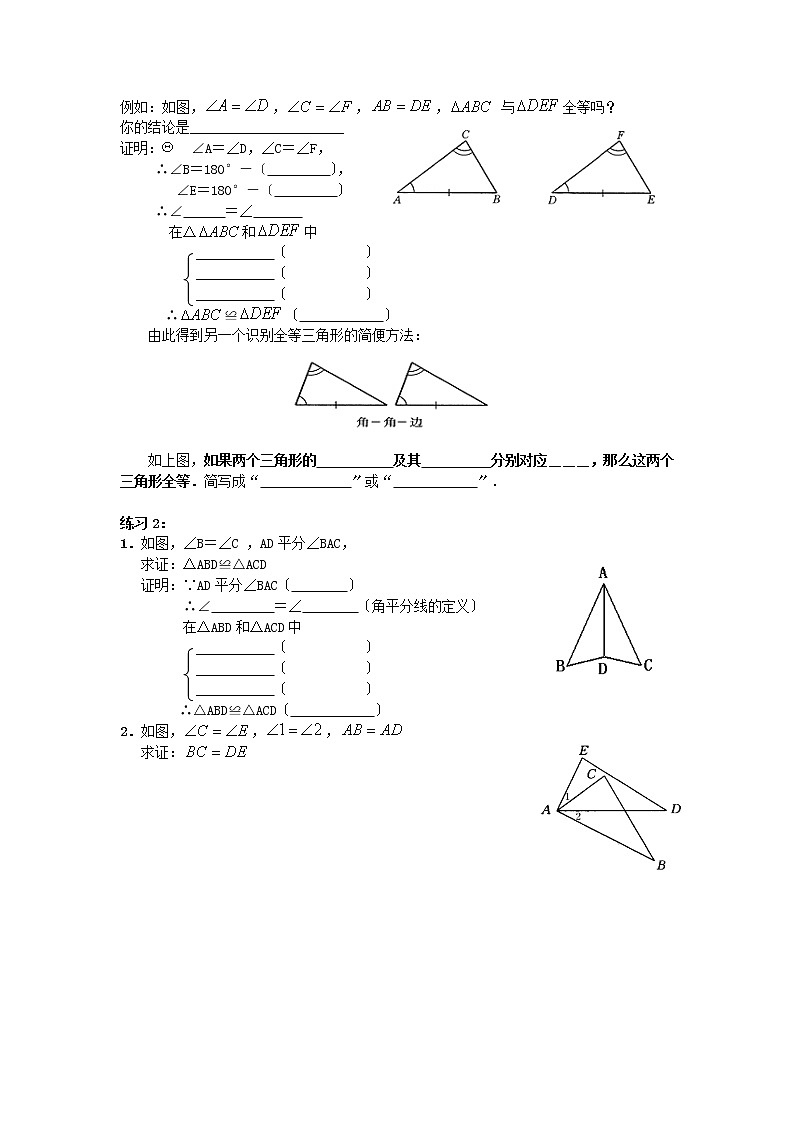
例如：如图，，，， 与全等吗？
你的结论是______________________
证明： ∠A＝∠D，∠C＝∠F，
∴∠B＝180°－〔 〕，
∠E＝180°－〔 〕
∴∠ ＝∠
在△和中
〔 〕
〔 〕
〔 〕
∴≌〔 〕
由此得到另一个识别全等三角形的简便方法：

如上图，如果两个三角形的 及其 分别对应＿＿＿，那么这两个三角形全等．简写成“ 〞或“ 〞．
练习2：
1．如图，∠B＝∠C ，AD平分∠BAC，
求证：△ABD≌△ACD
证明：∵AD平分∠BAC〔 〕
∴∠ ＝∠ 〔角平分线的定义〕
在△ABD和△ACD中
〔 〕
〔 〕
〔 〕
∴△ABD≌△ACD〔 〕
2．如图，，，
求证：
课堂检测：
1．如下图，在△ABC和△DEF中，AB=DE，∠B=∠E，要使△ABC≌△DEF，需要补充的一个条件是 〔只需填写一个即可〕．
2．如图，∠A＝∠D，∠1＝∠2，那么要得到△ABC≌△DEF，还应给出的条件是〔 〕。
〔A〕∠E＝∠B 〔B〕ED＝BC
〔C〕AB＝EF 〔D〕AF＝CD
3．如图，∠1＝∠2，∠B＝∠D，
求证：△ABC≌△ADC

4．如图，AB∥CD，∠A＝∠D，BF＝CE，∠AEB＝110°，
求∠DFC的度数
课后作业：
1．如图，在△ABC中，BE⊥AD于E，CF⊥AD于F，且BE＝CF，那么BD与DC相等吗？你能说明理由吗？
解：BD＝CD
理由：
∵BE⊥AD于E，CF⊥AD于F
∴∠ ＝∠ ＝90°〔垂直的定义〕
在△ 和△ 中
〔 〕
〔 〕
〔 〕
∴△ ≌△ 〔 〕
∴BD＝CD〔 〕
2．在△ABC中，，AD、BE分别是∠CAB、∠CBA的角平分线
求证：△ABD≌△BAE
3．： 如图，∠C＝∠D，CE＝DE．
求证： ∠DAB＝∠ABC．