数学11.1.2 三角形的高、中线与角平分线图文ppt课件

这是一份数学11.1.2 三角形的高、中线与角平分线图文ppt课件，共14页。PPT课件主要包含了∠BAD＝∠CAD等内容，欢迎下载使用。

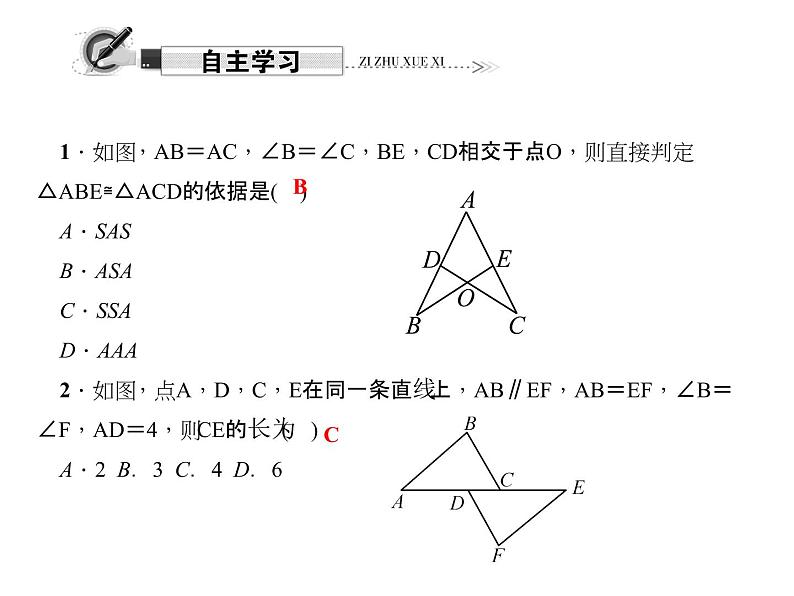
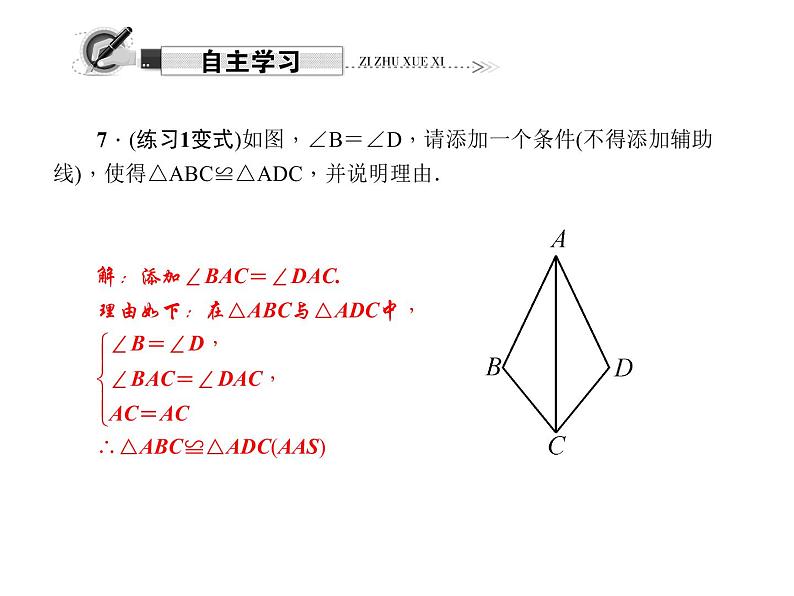
1．如图，AB＝AC，∠B＝∠C，BE，CD相交于点O，则直接判定△ABE≌△ACD的依据是( )A．SASB．ASAC．SSAD．AAA2．如图，点A，D，C，E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AD＝4，则CE的长为( )A．2 B．3 C．4 D．6
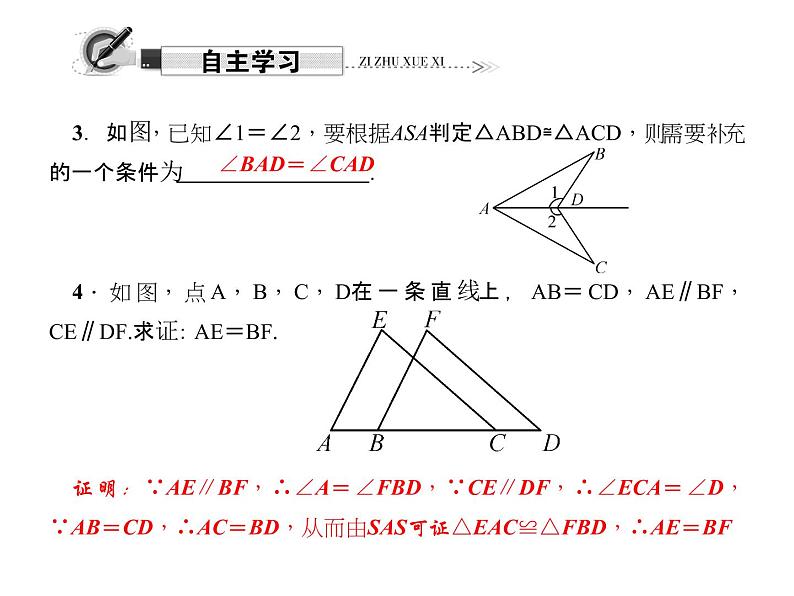
3．如图，已知∠1＝∠2，要根据ASA判定△ABD≌△ACD，则需要补充的一个条件为 ．4．如图，点A，B，C，D在一条直线上，AB＝CD，AE∥BF，CE∥DF.求证：AE＝BF.证明：∵AE∥BF，∴∠A＝∠FBD，∵CE∥DF，∴∠ECA＝∠D，∵AB＝CD，∴AC＝BD，从而由SAS可证△EAC≌△FBD，∴AE＝BF
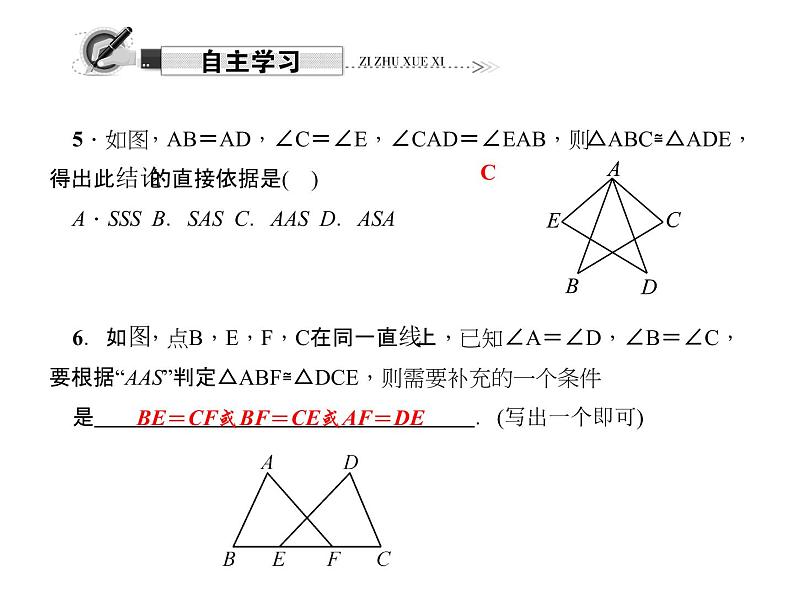
5．如图，AB＝AD，∠C＝∠E，∠CAD＝∠EAB，则△ABC≌△ADE，得出此结论的直接依据是( )A．SSS B．SAS C．AAS D．ASA6．如图，点B，E，F，C在同一直线上，已知∠A＝∠D，∠B＝∠C，要根据“AAS”判定△ABF≌△DCE，则需要补充的一个条件是 ．(写出一个即可)
BE＝CF或BF＝CE或AF＝DE
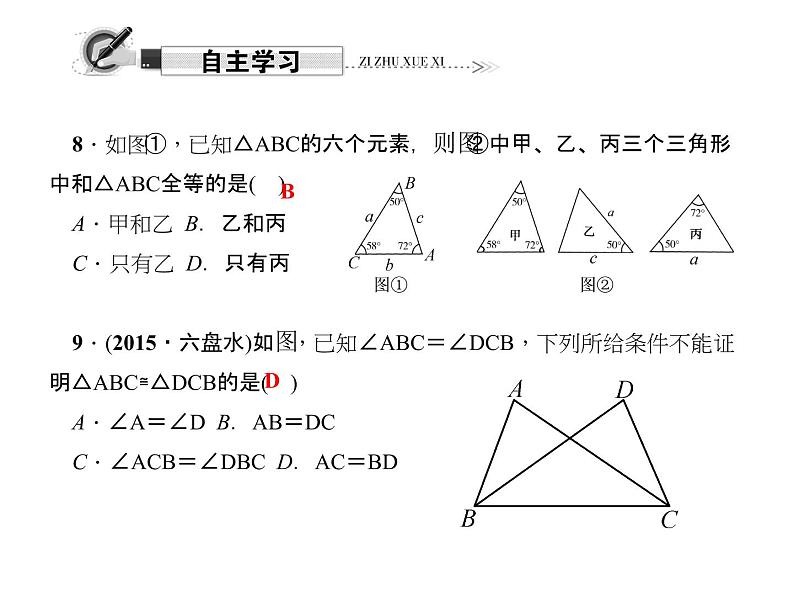
8．如图①，已知△ABC的六个元素，则图②中甲、乙、丙三个三角形中和△ABC全等的是( )A．甲和乙 B．乙和丙C．只有乙 D．只有丙9．(2015·六盘水)如图，已知∠ABC＝∠DCB，下列所给条件不能证明△ABC≌△DCB的是( )A．∠A＝∠D B．AB＝DCC．∠ACB＝∠DBC D．AC＝BD
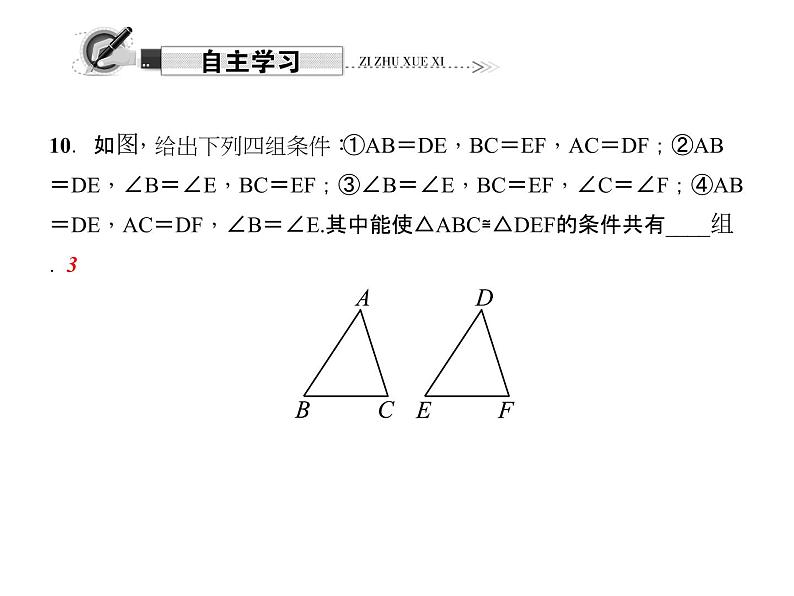
10．如图，给出下列四组条件：①AB＝DE，BC＝EF，AC＝DF；②AB＝DE，∠B＝∠E，BC＝EF；③∠B＝∠E，BC＝EF，∠C＝∠F；④AB＝DE，AC＝DF，∠B＝∠E.其中能使△ABC≌△DEF的条件共有____组．
11．如图，某同学把一个三角形玻璃打碎成三块，现在要到玻璃店去配一块大小完全一样的玻璃，那么最省事的办法是( )A．带①和②去 B．带①去C．带②去 D．带③去12．如图，已知AB∥CF，点E为DF的中点，若AB＝9 cm，CF＝5 cm，则BD的长度为____cm.
13．如图，在△ABC中，∠ACB＝90°，AC＝BC，AE是△ABC的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC，交CF的延长线于D.(1)求证：AE＝CD；(2)若AC＝12 cm，求BD的长．解：(1)由ASA证△ACE≌△CBD(2)BD＝6 cm
14．如图，在四边形ABCD中，点P是对角线BD上任意一点，∠1＝∠2，∠3＝∠4.求证：PA＝PC.解：先证△ABD≌△CBD(ASA)，再证△ABP≌△CBP(SAS)或△ADP≌△CDP(SAS)
15．如图，在△ABC中，∠B＝∠C，D，E，F分别在AB，BC，AC上，且BD＝CE，∠DEF＝∠B.求证：DE＝EF.证明：∵∠B＋∠BDE＝∠DEC＝∠DEF＋∠CEF，又∵∠B＝∠DEF，∴∠BDE＝∠CEF，又∵∠B＝∠C，BD＝CE，∴△BDE≌△CEF(ASA)，∴DE＝EF
16．在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E.(1)当直线MN绕点C旋转到图①的位置时，求证：DE＝AD＋BE；(2)当直线MN绕点C旋转到图②的位置时，求证：DE＝AD－BE；(3)当直线MN绕点C旋转到图③的位置时，试问DE，AD，BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
解：(1)证△ACD≌△CBE，∴DC＝BE，AD＝CE，∴DE＝DC＋CE＝AD＋BE(2)证法同(1)(3)DE＝BE－AD，证法同(1)