人教版八年级上册第十二章 全等三角形综合与测试随堂练习题
展开人教版数学八年级上册《全等三角形》证明题专项练习
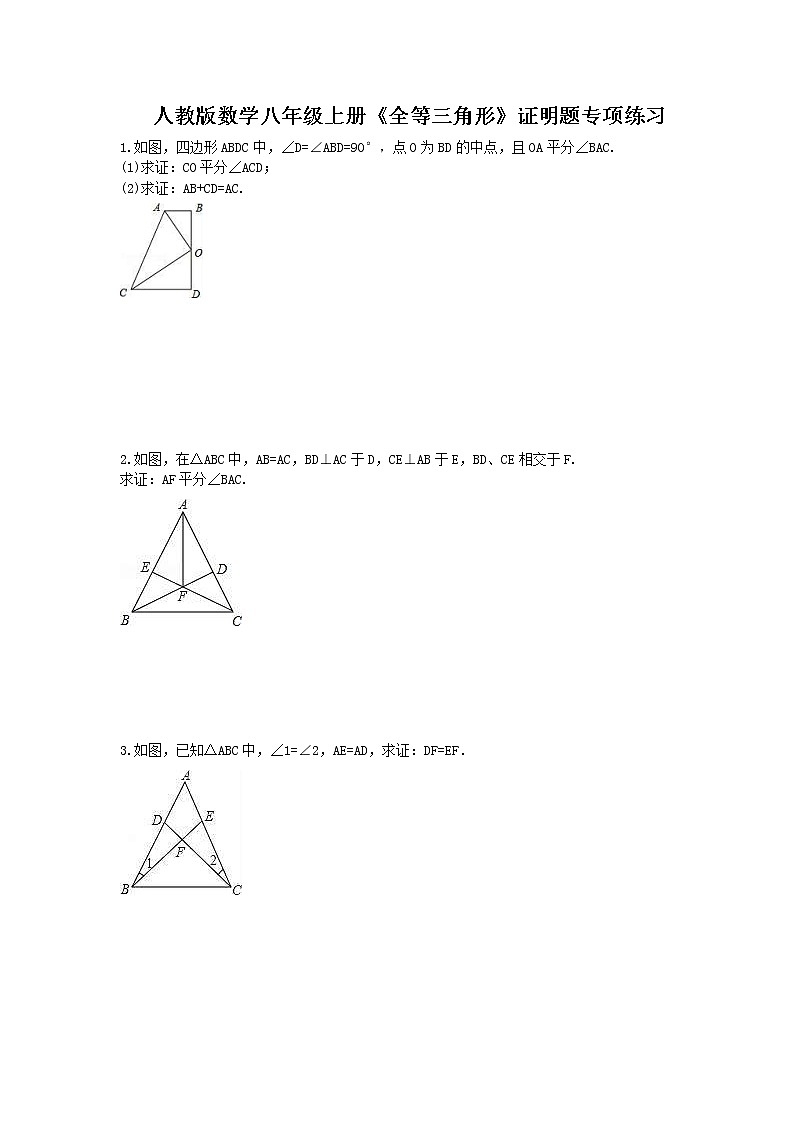
1.如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
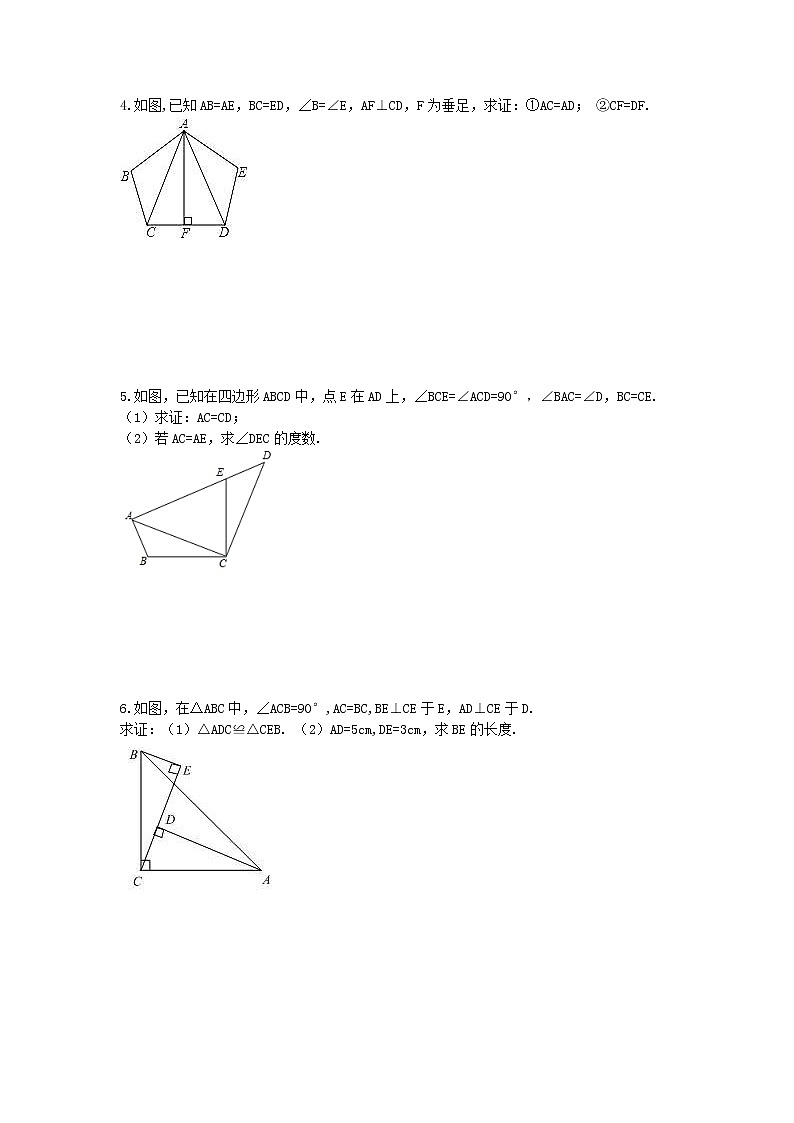
2.如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.
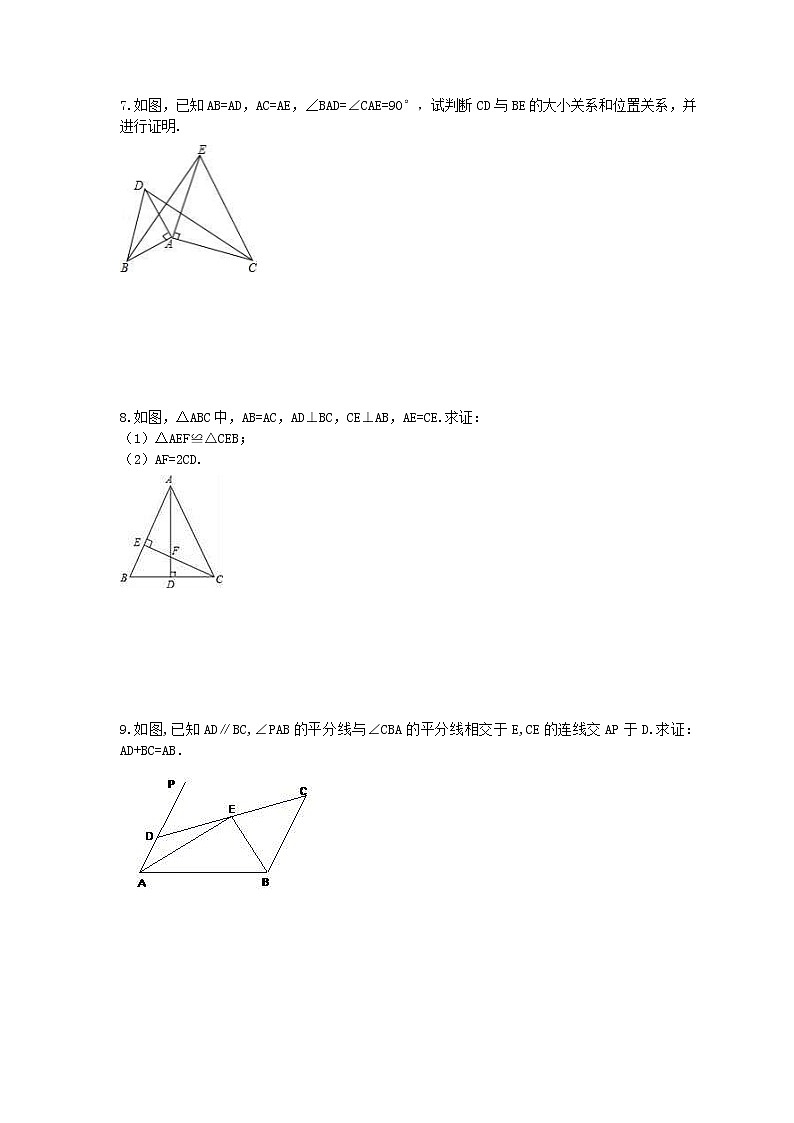
3.如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.
4.如图,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:①AC=AD; ②CF=DF.
5.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
6.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
求证:(1)△ADC≌△CEB. (2)AD=5cm,DE=3cm,求BE的长度.
7.如图,已知AB=AD,AC=AE,∠BAD=∠CAE=90°,试判断CD与BE的大小关系和位置关系,并进行证明.
8.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
9.如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.
10.如图,AD平分∠BAC,EF垂直平分AD交BC的延长线于F,连接AF.求证:∠B=∠CAF.
11.如图,△ABC中,AD是∠CAB的平分线,且AB=AC+CD.
求证:∠C=2∠B
12.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
13.如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
(1)若∠ABE=60°,求∠CDA的度数.
(2)若AE=2,BE=1,CD=4.求四边形AECD的面积.
14.如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20, BE=4,求AB的长.
参考答案
1.证明:(1)过O点作OE⊥AC于点E.∵∠ABD=90°且OA平分∠BAC∴OB=OE,
又∵O是BD中点∴OB=OD,∴OE=OD,
∵OE⊥AC,∠D=90°∴点O在∠ACD 的角平分线上∴OC平分∠ACD.
(2)在Rt△ABO和Rt△AEO中
∵∴Rt△ABO≌Rt△AEO(HL),∴AB=AE,
在Rt△CDO和Rt△CEO中∵∴Rt△CDO≌Rt△CEO(HL),
∴CD=CE,∴AB+CD=AE+CE=AC.
2.证明:∵AB=AC(已知),∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,∴BD⊥AC,CE⊥AB(高的定义).∴∠CEB=∠BDC=90°.
∴∠ECB=90°﹣∠ABC,∠DBC=90°﹣∠ACB.
∴∠ECB=∠DBC(等量代换).∴FB=FC(等角对等边),
在△ABF和△ACF中,,∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),∴AF平分∠BAC.
3.证明:在△ABE和△ACD中,,∴△ABE≌△ACD(AAS),∴AB=AC,
∵AE=AD,∴AB﹣AD=AC﹣AE,即BD=CE,
在△BDF和△CEF中,,∴△BDF≌△CEF(AAS),∴DF=EF.
4.证明:①∵AB=AE,BC=ED,∠B=∠E,∴△ABC≌△AED(SAS),∴AC=AD,
②∵AF⊥CD,AC=AD,∴CF=FD(三线合一性质).
5.解:∵∠BCE=∠ACD=90°,
∴∠3+∠4=∠4+∠5,
∴∠3=∠5,
在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,
∵∠BAE=∠1+∠2=90°,
∴∠1=∠D,
在△ABC和△DEC中,
∠1=∠D,∠3=∠5,BC=CE,
∴△ABC≌△DEC(AAS),
∴AC=CD;
(2)∵∠ACD=90°,AC=CD,
∴∠2=∠D=45°,
∵AE=AC,
∴∠4=∠6=67.5°,
∴∠DEC=180°-∠6=112.5°.
6.(1)证明:如图,∵AD⊥CE,∠ACB=90°,∴∠ADC=∠ACB=90°,
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中,
∠ADC=∠CEB,∠CAD=∠BCE,AC=BC,
∴△ADC≌△CEB(AAS);
(2)由(1)知,△ADC≌△CEB,则AD=CE=5cm,CD=BE.
如图,∵CD=CE-DE,∴BE=AD-DE=5-3=2(cm),即BE的长度是2cm.
7.证明:CD=BE,CD⊥BE,理由如下:
因为∠BAD=∠CAE=90°,所以∠BAD+∠DAE=∠CAE+∠DAE,即∠BAE=∠DAC.
因为,所以△BAE≌△DAC(SAS).所以BE=DC,∠BEA=∠DCA.
如图,设AE与CD相交于点F,因为∠ACF+∠AFC=90°,∠AFC=∠DFE,
所以∠BEA+∠DFE=90°.即CD⊥BE.
8.(1)证明:由于AB=AC,故△ABC为等腰三角形,∠ABC=∠ACB;
∵AD⊥BC,CE⊥AB,
∴∠AEC=∠BEC=90°,∠ADB=90°;
∴∠BAD+∠ABC=90°,∠ECB+∠ABC=90°,
∴∠BAD=∠ECB,
在Rt△AEF和Rt△CEB中
∠AEF=∠CEB,AE=CE,∠EAF=∠ECB,
所以△AEF≌△CEB(ASA)
(2)∵△ABC为等腰三角形,AD⊥BC,
故BD=CD,即CB=2CD,
又∵△AEF≌△CEB,
∴AF=CB=2CD.
9.证明:做BE的延长线,与AP相交于F点,
∵PA//BC
∴∠PAB+∠CBA=180°,又∵,AE,BE均为∠PAB和∠CBA的角平分线
∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB为直角三角形
在三角形ABF中,AE⊥BF,且AE为∠FAB的角平分线
∴三角形FAB为等腰三角形,AB=AF,BE=EF
在三角形DEF与三角形BEC中,
∠EBC=∠DFE,且BE=EF,∠DEF=∠CEB,
∴三角形DEF与三角形BEC为全等三角形,∴DF=BC
∴AB=AF=AD+DF=AD+BC.
10.证明:∵EF垂直平分AD,∴AF=DF,∠ADF=∠DAF,
∵∠ADF=∠B+∠BAD,∠DAF=∠CAF+∠CAD,
又∵AD平分∠BAC,∴∠BAD=∠CAD,
∴∠B=∠CAF.
11.证明:延长AC至E,使CE=CD,连接ED
∵AB=AC+CD
∴AE=AB
∵AD平分∠CAB
∴∠EAD=∠BAD
∴AE=AB,∠EAD=∠BAD,AD=AD
∴△ADE≌△ADB
∴∠E=∠B且∠ACD=∠E+∠CDE,CE=CD
∴∠ACD=∠E+∠CDE=2∠E=2∠B
即∠C=2∠B.
12. (1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,
,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
13.解:(1)∵AC平分∠BCD,AE⊥BC AF⊥CD,
∴AE=AF,
在Rt△ABE和Rt△ADF中,AE=AF,AB=AD.
∴Rt△ABE≌Rt△ADF,
∴∠ADF=∠ABE=60°,
∴∠CDA=180°﹣∠ADF=120°;
(2)由(1)知:Rt△ABE≌Rt△ADF,
∴FD=BE=1,AF=AE=2,CE=CF=CD+FD=5,
∴BC=CE+BE=6,
∴四边形AECD的面积=△ABC的面积+△ACD的面积=10.
14.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中
BD=CD,BE=CF.
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)解:∵Rt△BED≌Rt△CFD,
∴AE=AF,CF=BE=4,
∵AC=20,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.
【期中复习】人教版 初中数学八年级上册数学期末全等三角形证明题专题训练(含解析): 这是一份【期中复习】人教版 初中数学八年级上册数学期末全等三角形证明题专题训练(含解析),共26页。试卷主要包含了如图,,M是的中点,,连接,如图,四边形中,,平分,于点E,已知,如图,与中,与交于点E,且,等内容,欢迎下载使用。
人教版数学九年级上册专项培优练习十六《切线的性质与判定证明题专练》(含答案): 这是一份人教版数学九年级上册专项培优练习十六《切线的性质与判定证明题专练》(含答案),共19页。
人教版数学八年级上册专项培优练习四《全等三角形证明题专练》(含答案): 这是一份人教版数学八年级上册专项培优练习四《全等三角形证明题专练》(含答案),共14页。













