初中数学北师大版九年级上册第一章 特殊平行四边形3 正方形的性质与判定一课一练

1.3 《正方形的性质与判定》习题2

一、选择题

1．小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得∠B＝60°，对角线AC＝20cm，接着活动学具成为图2所示正方形，则图2中对角线AC的长为(　　)

A．20cm B．30cm C．40cm D．20cm

2．如图，P为正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF．给出以下4个结论：①△FPD是等腰直角三角形；②AP＝EF；③AD＝PD；④∠PFE＝∠BAP．其中，所有正确的结论是(　　)

A．①② B．①④ C．①②④ D．①③④

3.已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是( )

A．选①② B．选②③ C．选①③ D．选②④

4.如图，已知四边形ABCD是平行四边形，下列结论中错误的是(　　)

A．当AB=BC时，它是菱形 B．当AC⊥BD时，它是菱形

C．当AC=BD时，它是矩形 D．当∠ABC=90°时，它是正方形

二、填空题

1.如图，已知P是正方形ABCD对角线BD上一点，且BP = BC，则∠DCP度数是_________．

2.如图，为正方形内部一点，且，，，则阴影部分的面积为_______．

3.用边长为1的正方形做了一套七巧板，拼成如图所示的一座桥，则桥中阴影部分的面积为原正方形面积的__________．

4.如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=2，CE=6，H是AF的中点，那么CH的长是               ．

三、解答题

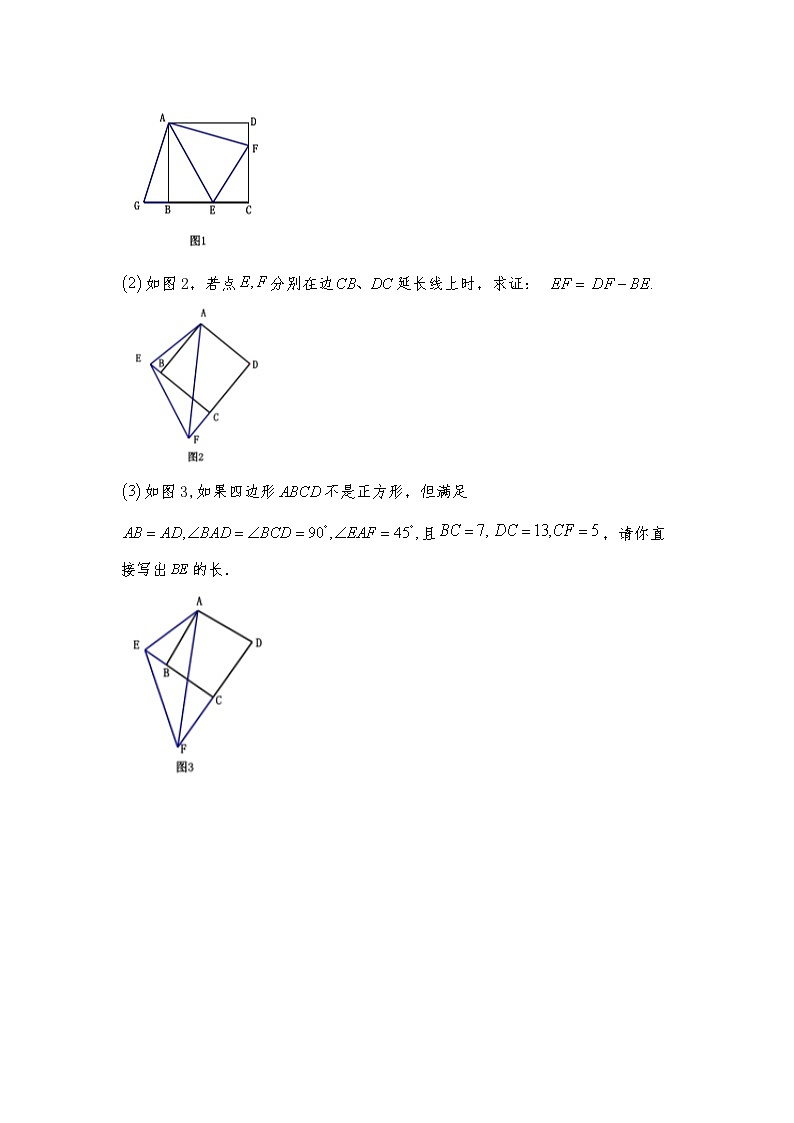
1.已知如图1,四边形是正方形， ．

如图1,若点分别在边上,延长线段至,使得,若求的长；

如图2，若点分别在边延长线上时，求证：

如图3,如果四边形不是正方形，但满足且，请你直接写出的长．

2.如图，正方形ABCD中，E为BC上一点，过点B作于G，延长BG至点F使．

(1)求证：；

(2)求证：；

(3)若，求AB的长．

3.如图，四边形ABCD是边长为1的正方形，为等边三角形，求的面积．

4.如图1，点C在线段AB上，分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN， 连结AM、BD． 

(1)AM与BD的关系是：________．   

(2)如果将正方形BCMN绕点C顺时针旋转锐角α(如图2)．(1) 中所得的结论是否仍然成立？请说明理由．   

(3)在(2)的条件下，连接AB、DM，若AC=4，BC=2，求AB2+DM2的值．

5.如图l，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AMBE，垂足为M，AM交BD于点F．

(1)求证：OE=OF；

(2)如图2，若点E在AC的延长线上，AMBE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗．如果成立，请给出证明；如果不成立，请说明理由．

6.如图，在一次数学兴趣小组活动中，一位同学用直尺和圆规对矩形进行了如下操作：

①作的平分线交于点；

②过点作交于点过点作交于点．

请你根据操作，观察图形解答下列问题：

(1)求证：四边形为正方形；

(2)若，求四边形的面积．

7.如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF， 则下列结论：

①△EBF≌△DFC；

②四边形AEFD为平行四边形；

③当AB=AC，∠BAC=1200时，四边形AEFD是正方形．

其中正确的结论是         ．(请写出正确结论的番号)．

8.如图，菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上，连接CF．

(1)求证：∠HEA=∠CGF；

(2)当AH=DG时，求证：菱形EFGH为正方形．

9.在△ABC中，AB=AC，D是BC的中点，DE⊥AB， DF⊥AC，垂足分别是E，F.

(1)证明：DE=DF；

(2)只添加一个条件，使四边形EDFA是正方形.并证明结论.

10.四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交线段BC于点F，以DE、EF为邻边作矩形DEFG，连接CG

(1)如图，求证：矩形DEFG是正方形；

(2)若AB＝2，CE＝2，求CG的长；

11.如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE，

(1)求证：四边形AEBD是矩形；

(2)当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由．

12.如图，正方形ABCD中， AB＝4， 点E是对角线AC上的一点，连接DE，过点E作EF⊥ED，交AB于点F，以DE、EF为邻边作矩形DEFG，连接AG．

(1)求证：矩形DEFG是正方形．

(2)求AG＋AE的值．

13.如图，是等腰三角形，AB=CD，点D是点B关于AC对称的点．

(1)如图一，若，请利用尺规作图作点D，连接AD、CD，求证：四边形ABCD是正方形．(保留作图痕迹)

(2)如图二，连接AD、CD，四边形ABCD为菱形，点E是BC中点，点O是对角线AC与BD的交点，连接AE，若点O关于线段AE的对称点F在线段AB上，，，求AE的长．

答案

一、选择题

1．D．

2．C．

3.B．

4.D.

二、填空题

1.22.5°.

2.19．

3..

4.2．

三、解答题

1.解：(1)证明：如图1所示，在正方形ABCD中，AB=AD，∠BAD=90°，

在ABG和ADF中，

∴ABG≌ADF(SAS)，

∴AG=AF，∠BAG=∠DAF，

又∵∠DAF+∠FAB=∠FAB+∠BAG=90°，且∠EAF=45°，

∴∠EAG=∠FAG-∠EAF=45°=∠EAF，

在GAE和FAE中，

∴GAE≌FAE(SAS)，

∴EF=GE=GB+BE=2+3=5；

(2)如下图所示，在DF上取一点G,使得DG=BE, 连接AG，

∵四边形ABCD是正方形，故AB=AD，∠ABE=∠ADG=90°，

在ABE和ADG中，

∴ABE≌ADG(SAS)，

∴AE=AG，∠BAE=∠DAG，

∵∠BAG+∠DAG=90°，故∠BAG+∠BAE=90°，

∵∠EAF=45°，故∠GAF=45°，∠EAF=∠GAF=45°，

在AEF和AGF中，

∴AEF≌AGF(SAS)，

∴EF=GF，且DG=BE，

∴EF=DF-DG=DF-BE；

(3)BE=5，

如下图所示，在线段DF上取BE=DG，连接AG，

∵∠BAD=∠BCD=90°，故∠ABC+∠ADC=180°，且∠ABC+∠ABE=180°，

∴∠ABE=∠ADC，

在ABE和ADG中，

∴ABE≌ADG(SAS)，

∴AE=AG，∠BAE=∠DAG，

∵∠BAG+∠DAG=90°，故∠BAG+∠BAE=90°，

∵∠EAF=45°，故∠GAF=45°，∠EAF=∠GAF=45°，

在AEF和AGF中，

∴AEF≌AGF(SAS)，

∴EF=GF，

设BE=x，则CE=BC+BE =7+x，EF=GF=DC+CF-DG= DC+CF-BE=18-x，

在直角三角形ECF中，根据勾股定理：，

即：，解得x=5，

∴BE=x=5．

2.(1)证明：因为ABCD是正方形

所以

在三角形BGA中，

因为

(2)过点C作，

因为ABCD是正方形，

所以AB=BC，

由(1)

所以

在三角形CHF中，

，

所以．

(3)在三角形CHF中，

．

3.解：如图所示：
 

过P作PE⊥CD于E，PF⊥BC于F，
则PE=FC，∠PEC=∠PFC=90°，
∵正方形ABCD的边长是1，△BPC为正三角形，
∴∠BCD=90°，∠PBC=∠PCB=60°，PB=PC=BC=CD=1，
∴四边形CEPF是矩形，
∴PE=FC，
∵PF⊥BC，
∴BF=FC=BC=，
∴PE=FC=，
由勾股定理得：，
 

4.(1)相等且垂直.

(1)在正方形ACDE和正方形BCMN中，

∵AC=DC，∠ACM=∠DCB=90°，CM=CB，

∴△ACM≌△DCB(SAS)，

∴AM=BD，∠MAC=∠BDC，

∵∠MAC+∠AMC=90°，

∴∠MAC+∠DBC=90°，

∴AM⊥BD；

故答案为相等且垂直；

(2)第(1)问中的结论仍然成立，即AM与BD的关系是：相等且垂直；理由如下：

如图所示，设AM与CD交于点P，

在正方形ACDE和正方形BCMN中，

∵AC=DC，∠ACD=∠MCB=90°，CM=CB，

∴∠ACD+∠DCM=∠MCB+∠DCM,

即∠ACM=∠DCB，

∴△ACM≌△DCB(SAS)，

∴AM=BD，∠MAC=∠BDC，

∵∠MAC+∠APC=90°，

∴∠BDC+∠APC =90°，

∵∠APC =∠DPM，

∴∠BDC+∠DPM =90°，

∴AM⊥BD；

∴AM与BD的关系是：相等且垂直；

(3)如图所示，连接AD、BM，设AM与BD交于点Q，

∵AC=4，BC=2，

∴AD2=42+42=32，BM2＝22+22＝8，

∴，，

由(2)可知，AM⊥BD，

∴AB2=AQ2+BQ2，DM2=DQ2+MQ2；AD2=AQ2+DQ2，BM2=BQ2+MQ2，

∴AB2+DM2＝AQ2+BQ2+DQ2+MQ2，

AD2+BM2＝AQ2+DQ2+BQ2+MQ2，

∴AB2+DM2＝AD2+BM2=40.

5.解：(1)∵四边形ABCD是正方形．

∴∠BOE＝∠AOF＝90°，OB＝OA，

又∵AM⊥BE，

∴∠MEA＋∠MAE＝90°＝∠AFO＋∠MAE

∴∠MEA＝∠AFO，

∴Rt△BOE≌ Rt△AOF

∴OE＝OF

(2)OE＝OF成立

∵四边形ABCD是正方形，

∴∠BOE＝∠AOF＝90°，OB＝OA

又∵AM⊥BE，

∴∠F＋∠MBF＝90°＝∠E＋∠OBE

又∵∠MBF＝∠OBE

∴∠F＝∠E

∴Rt△BOE≌Rt△AOF

∴OE＝OF

6.(1)∵四边形ABCD是矩形；

，

又∵AE平分

又

∴四边形ABEF是矩形，

又

∴四边形ABEF是正方形；

(2)连接DE

，四边形ABEF是正方形，

又

∴S四边形DHEC=

7.∵△ABE、△BCF为等边三角形，∴AB=BE=AE，BC=CF=FB，∠ABE=∠CBF=60°，∴∠ABE﹣∠ABF=∠FBC﹣∠ABF，即∠CBA=∠FBE，在△ABC和△EBF中，∵AB=EB，∠CBA=∠FBE，BC=BF，∴△ABC≌△EBF(SAS)，选项①正确；

∴EF=AC，又∵△ADC为等边三角形，∴CD=AD=AC，∴EF=AD，同理可得AE=DF，∴四边形AEFD是平行四边形，选项②正确；

若AB=AC，∠BAC=120°，则有AE=AD，∠EAD=120°，此时AEFD为菱形，选项③错误，

故答案为①②．

8.解：(1)连接GE，

∵AB∥CD，

∴∠AEG=∠CGE，

∵GF∥HE，

∴∠HEG=∠FGE，

∴∠HEA=∠CGF；

(2)∵四边形ABCD是正方形，

∴∠D=∠A=90°，

∵四边形EFGH是菱形，

∴HG=HE，

在Rt△HAE和Rt△GDH中，

∴Rt△HAE≌Rt△GDH(HL)，

∴∠AHE=∠DGH，又∠DHG+∠DGH=90°，

∴∠DHG+∠AHE=90°，

∴∠GHE=90°，

∴菱形EFGH为正方形．

9.解：(1) ∵AB=AC，∠B=∠C ，

∵DE⊥ AB，DF⊥ AC ，

∴∠DEB=∠DFC= 90°，

∵D是BC的中点，

∴BD=DC ，  

∴△BDE≌△CDF ，

∴DE=DF；

(2)∠A=90°，

∵DE⊥ AB，DF⊥ AC  ，

∴∠DEB=∠DFC= 90° ，

又∵∠A=90°，

∴∠DEB=∠DFC=∠A=90°，

∴四边形AEDF是矩形，

又∵DE=DF，

∴矩形AEDF是正方形.

10.(1)证明：作EP⊥CD于P，EQ⊥BC于Q，

∵∠DCA＝∠BCA，

∴EQ＝EP，

∵∠QEF+∠FEC＝45°，∠PED+∠FEC＝45°，

∴∠QEF＝∠PED，             

在Rt△EQF和Rt△EPD中，，

∴Rt△EQF≌Rt△EPD(ASA)，

∴EF＝ED，

∴矩形DEFG是正方形；

(2)如图2中，在Rt△ABC中．AC＝AB＝4，

计算得EC＝2，

∴AE＝CE，

∴点F与C重合，此时△DCG是等腰直角三角形，易知CG＝2；

11.(1)证明：∵点O为AB的中点，连接DO并延长到点E，使OE=OD，

∴四边形AEBD是平行四边形，

∵AB=AC，AD是∠BAC的角平分线，

∴AD⊥BC，

∴∠ADB=90°，

∴平行四边形AEBD是矩形；

(2)当∠BAC=90°时，

理由：∵∠BAC=90°，AB=AC，AD是∠BAC的角平分线，

∴AD=BD=CD，

∵由(1)得四边形AEBD是矩形，

∴矩形AEBD是正方形．

12.解：(1)如图，作于，于．

∵四边形是正方形，

，

∵于，于，

，

∵，

四边形是矩形，

∵，

，

，

∵，

，

，

∵四边形是矩形，

四边形是正方形．

(2)∵四边形是正方形，四边形是正方形，

，，，

，

，

，

．

13.解：(1)如图，即为所作图形，

∵点D和点B关于AC对称，

∴AB=AD，CB=CD，

∵AB=CD，

∴AB=AD=CB=CD，

∴四边形ABCD是菱形，

又∵∠ABC=90°，

∴四边形ABCD为正方形；

(2)∵点E是BC中点，EF⊥BD，

∴EF是△ABC的中位线，即点F为AB中点，

∵点F和点O关于AE对称，

∴AO=AF，

∵四边形ABCD是菱形，

∴AO=CO，

∴AB=AC=BC，

∴△ABC是等边三角形，而AE和BO都是△ABC的中线，

∴AE=BO，

∵，

∴AE=BO=．