高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系课前预习课件ppt

这是一份高中数学人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系课前预习课件ppt，共19页。PPT课件主要包含了②没有公共点，两直线平行，两直线为异面直线，两直线相交，①在同一平面内，异面直线所成的角，1复习回顾，1范围，达标检测等内容，欢迎下载使用。

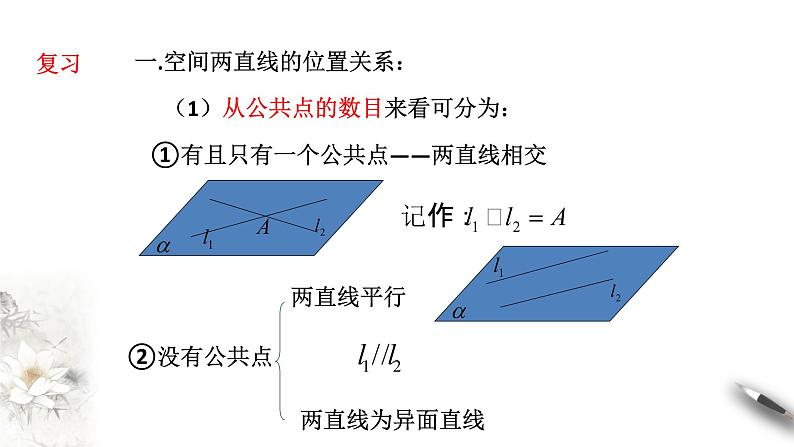
一.空间两直线的位置关系：
（1）从公共点的数目来看可分为：
①有且只有一个公共点——两直线相交
（2）从平面的性质 来讲，可分为：
②不同在任何一个平面内——两直线为异面直线。
如图，在正方体 中，直线 与直线AB，直线 与直线AB都是异面直线，直线 与 相对于直线AB的位置相同吗？如果不同，如何表示这种差异呢？
在平面内,两条直线相交成四个角, 其中不大于90度的角称为它们的夹角, 用以刻画两直线的错开程度, 如图.
思考：异面直线有没有夹角呢？若有，那如何找 出这个夹角？
异面直线所成角的定义: 如图,已知两条异面直线a，b,经过空间任一点O作直线a′//a，b′//b,则把a′与b′所成的锐角(或直角)叫做异面直线所成的角(或夹角).
思考 : 这个角的大小与O点的位置有关吗 ? 即O点位置不同时, 这一角的大小是否改变?
（1）将空间图形转化为平面图形（2）异面直线夹角转化为相交直 线的夹角
(2)如果θ=90º ，我们就称这两条直线互相垂直 , 记为a ⊥ b.
例1 如图，已知正方体ABCD－A′B′C′D′.（1）哪些棱所在的直线与直线AA′垂直？ （2）求直线BA′与CC′所成的角大小。 （3）求直线BA′与AC 所成的角大小。
（3）如图，连接 ，因为 是正方体，所以 ，从而四边形 是平行四边形，所以 。于是 为异面直线BA′与AC所成的角。
连接 ，易知 是等边三角形，所以 ，从而异面直线BA′与AC 所成的角等于
例2 如图，在正方体 中， 为底面 的中心。求证： 。
证明：如图，连接 。 是正方体。
四边形 是平行四边形。
所以，直线 与 所成的角即为直线 与 所成的角。
连接 ，易证 。
又 为底面 的中心，
因为， 为 的中点，