高中数学人教A版 (2019)必修 第一册2.2 基本不等式教学设计

《2020-2021学年高一数学同步讲练测（新教材人教A版必修第一册）》

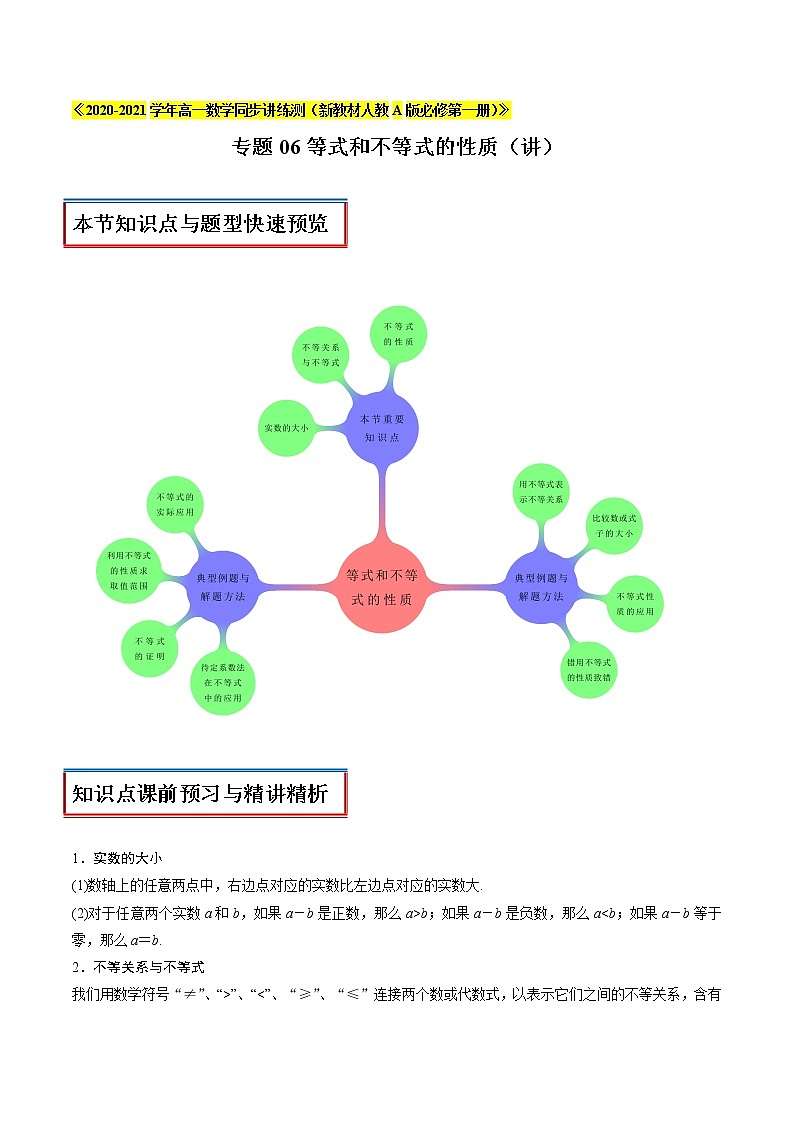
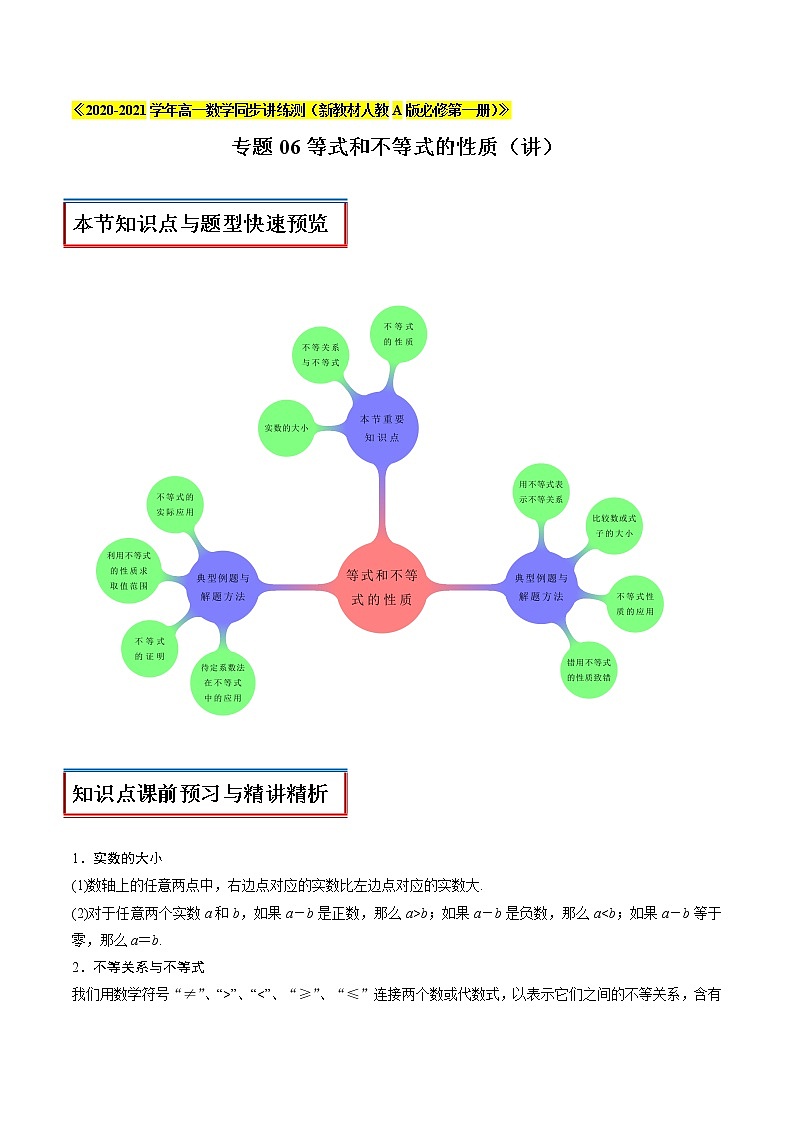
专题06等式和不等式的性质（讲）

1．实数的大小

(1)数轴上的任意两点中，右边点对应的实数比左边点对应的实数大.

(2)对于任意两个实数a和b，如果a－b是正数，那么a>b；如果a－b是负数，那么a<b；如果a－b等于零，那么a＝b.

2．不等关系与不等式

我们用数学符号“≠”、“>”、“<”、“≥”、“≤”连接两个数或代数式，以表示它们之间的不等关系，含有这些符号的式子，叫做不等式.

3．不等式的性质

(1)性质1：如果a>b，那么b<a；

如果b<a，那么a>b.

即a>b⇔b<a.

(2)性质2：如果a>b，b>c，那么a>c.

即a>b，b>c⇒a>c.

(3)性质3：如果a>b，那么a＋c>b＋c.

(4)性质4：①如果a>b，c>0那么ac>bc.

②如果a>b，c<0，那么ac<bc.

(5)性质5：如果a>b，c>d，那么a＋c>b＋d.

(6)性质6：如果a>b>0，c>d>0，那么ac>bd.

(7)性质7：如果a>b>0，那么an>bn，(n∈N，n≥2)．

(8)性质8：如果a>b>0，那么>，(n∈N，n≥2)．

1．下列四个命题：①若，则；②若，则；③若，则；④若，，则．其中真命题的个数是（    ）

A．1个 B．2个 C．3个 D．4个

2．元旦将近，调查鲜花市场价格得知：购买2只玫瑰与1只康乃馨所需费用之和大于8元，而购买4只玫瑰与5只康乃馨所需费用额小于22元；设购买2只玫瑰花所需费用为元，购买3只康乃馨所需费用为元，则的大小关系是（    ）．

A． B． C． D．的大小关系不确定

3．若，则下列不等式一定成立的是（    ）

A． B． C． D．

4．设，且，则，，，四个数中最小的数是（    ）

A． B． C． D．

5．已知，，则、 的大小关系为（    ）

A． B． C． D．无法确定

重要考点一：用不等式表示不等关系

【典型例题】一家银行的信贷部计划年初投入25000000元用于企业和个人贷款,希望这笔资金至少可带来30000元的收益,其中从企业贷款中获益12%,从个人贷款中获益10%.那么信贷部应该如何分配资金呢?用不等关系表示.

【题型强化】如图是在北京召开的第24界国际数学家大会的会标，会标是根据中国古代数学家赵爽的弦图设计的，颜色的明暗使它看上去象一个风车，代表中国人民热情好客．你能在这个图案中找出一些相等关系或不等关系吗？（教师引导学生从面积的关系去找相等关系或不等关系）．

【收官验收】日常生活中，在一杯含有克糖的克糖水中，再加入克糖，则这杯糖水变甜了.请根据这一事实提炼出一道不等式，并加以证明.

【名师点睛】

用不等式(组)表示实际问题中不等关系的步骤：

①审题．通读题目，分清楚已知量和待求量，设出待求量．找出体现不等关系的关键词：“至少”“至多”“不少于”“不多于”“超过”“不超过”等．

②列不等式组：分析题意，找出已知量和待求量之间的约束条件，将各约束条件用不等式表示．

重要考点二：比较数或式子的大小

【典型例题】已知，试比较与的大小.

【题型强化】已知，，试比较与的大小．

【收官验收】（1）比较与的大小，其中；

（2）设，，，比较与的大小.

【名师点睛】

比较两个实数(或代数式)大小的步骤

(1)作差：对要比较大小的两个数(或式子)作差；

(2)变形：对差进行变形(因式分解、通分、配方等)；

(3)判断差的符号：结合变形的结果及题设条件判断差的符号；

(4)作出结论．

这种比较大小的方法通常称为作差比较法．其思维过程：作差→变形→判断符号→结论，其中变形是判断符号的前提．

重要考点三：不等式性质的应用

【典型例题】若、、，且，则下列不等式中一定成立的是（    ）

A． B． C． D．

【题型强化】若，则下列不等式中不成立的是（    ）

A． B． C． D．

【收官验收】已知a，b，c，d∈R，则下列不等式中恒成立的是（　　）

A．若a＞b，c＞d，则ac＞bd B．若a＞b，则

C．若a＞b＞0，则（a﹣b）c＞0 D．若a＞b，则a﹣c＞b﹣c

【名师点睛】

不等式性质的应用主要有：判断不等式的真假，证明不等式，求参数的取值范围等．

1．判断不等式的真假．

(1)首先要注意不等式成立的条件，不要弱化条件．

(2)解决有关不等式选择题时，也可采用特值法进行排除，注意取值要遵循以下原则：一是满足题设条件；二是取值要简单，便于验证计算．

(3)若要判断某结论正确，应说明理由或进行证明，推理过程应紧扣有关定理、性质等，若要说明某结论错误，只需举一反例．

2．证明不等式

(1)要在理解的基础上，记准、记熟不等式的性质并注意在解题中灵活准确地加以应用．

(2)应用不等式的性质进行推证时，应注意紧扣不等式的性质成立的条件，且不可省略条件或跳步推导，更不能随意构造性质与法则．

3．求取值范围

(1)建立待求范围的代数式与已知范围的代数式的关系，利用不等式的性质进行运算，求得待求的范围．

(2)同向(异向)不等式的两边可以相加(相减)，这种转化不是等价变形，如果在解题过程中多次使用这种转化，就有可能扩大其取值范围．

4．掌握各性质的条件和结论．在各性质中，乘法性质的应用最易出错，即在不等式的两边同时乘(除)以一个数时，必须能确定该数是正数、负数或零，否则结论不确定．

重要考点四：错用不等式的性质致错

【典型例题】已知，，求证：.

【题型强化】若，试比较的大小．

【收官验收】对于实数，判断下列命题的真假．

（1）若，则．

（2）若，则．

（3）若，则．

（4）若，则．

（5）若，则．

（6）若，，则．

重要考点五：待定系数法在不等式中的应用

【典型例题】设实数，满足，，求的最大值．

【题型强化】已知,且－4≤f(1)≤－1,－1≤f(2)≤5,求f(3)的取值范围.

【收官验收】已知，，求的取值范围．

重要考点六：不等式的证明

【典型例题】已知，．

（Ⅰ）证明：；

（Ⅱ）证明：．

【题型强化】若，，，求证：.

【收官验收】下面的问题与著名的柯西不等式有关，请你比较与的大小，并猜测更一般的结论（不必证明）．

【名师点睛】

证明不等式的常用方法有：

(1)作差法．

(2)作商法．比较a与b的大小时，先判断a与b的符号，利用a>b>0⇒>1,0>a>b⇒<1.

根据待求不等式的形式，多项式形式适用于作差法，比值形式、指数形式适用于作商法．

重要考点七：利用不等式的性质求取值范围

【典型例题】已知实数x，y满足，则的取值范围是__________．

【题型强化】已知,,则的取值范围为__________.

【收官验收】已知实数、，满足，则的取值范围是_____________.

【名师点睛】

求取值范围的问题要注意解题方法是否符合不等式的性质，是否使范围扩大或缩小．

重要考点八：不等式的实际应用

【典型例题】某学校组织老师去某地参观学习，需包车前往.甲车队说：“如领队买全票一张，其余人可享受7.5折优惠.”乙车队说：“你们属团体票按原价的8折优惠.”这两车队的原价、车型都是一样的.试根据去的老师人数，比较两车队的收费哪家更优惠.

【题型强化】火车站有某公司待运的甲种货物，乙种货物，现计划用A，B两种型号的货厢共50节运送这批货物，已知35t甲种货物和15乙种货物可装满一节A型货厢，25t甲种货物和35乙种货物可装满一节B型货厢，据此安排A，B两种货厢的节数，共有几种方案？若每节A型货厢的运费是0.5万元，每节B型货用的运费是0.8万元，哪种方案的运费较少？

【收官验收】甲、乙两车从A地沿同一路线到达B地，甲车一半时间的速度为a，另一半时间的速度为b；乙车一半路程的速度为a，另一半路程的速度为b．若，试判断哪辆车先到达B地．

【名师点睛】

“最优方案”问题，首先要设出未知量，搞清楚比较的对象，然后把这个未知量用其他的已知量表示出来，通过比较即可得出结论．