北师大版数学七年级下册单元检测卷 第五章 生活中的轴对称（测能力）

这是一份北师大版数学七年级下册单元检测卷 第五章 生活中的轴对称（测能力），共14页。
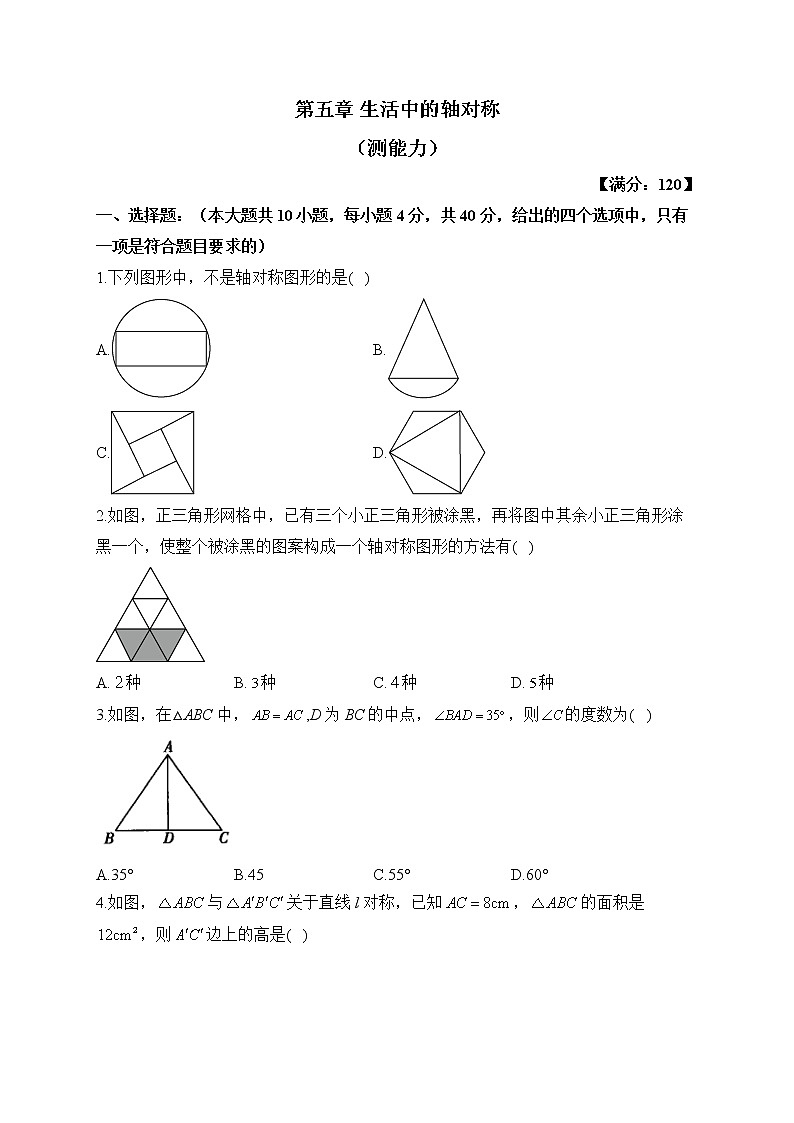
第五章   生活中的轴对称（测能力）【满分：120】一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）1.下列图形中，不是轴对称图形的是(   )A.  B. C.  D.2.如图，正三角形网格中，已有三个小正三角形被涂黑，再将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有(   )A.种 B.种 C.种 D.种3.如图，在△ABC中，,D为BC的中点，，则的度数为(   )

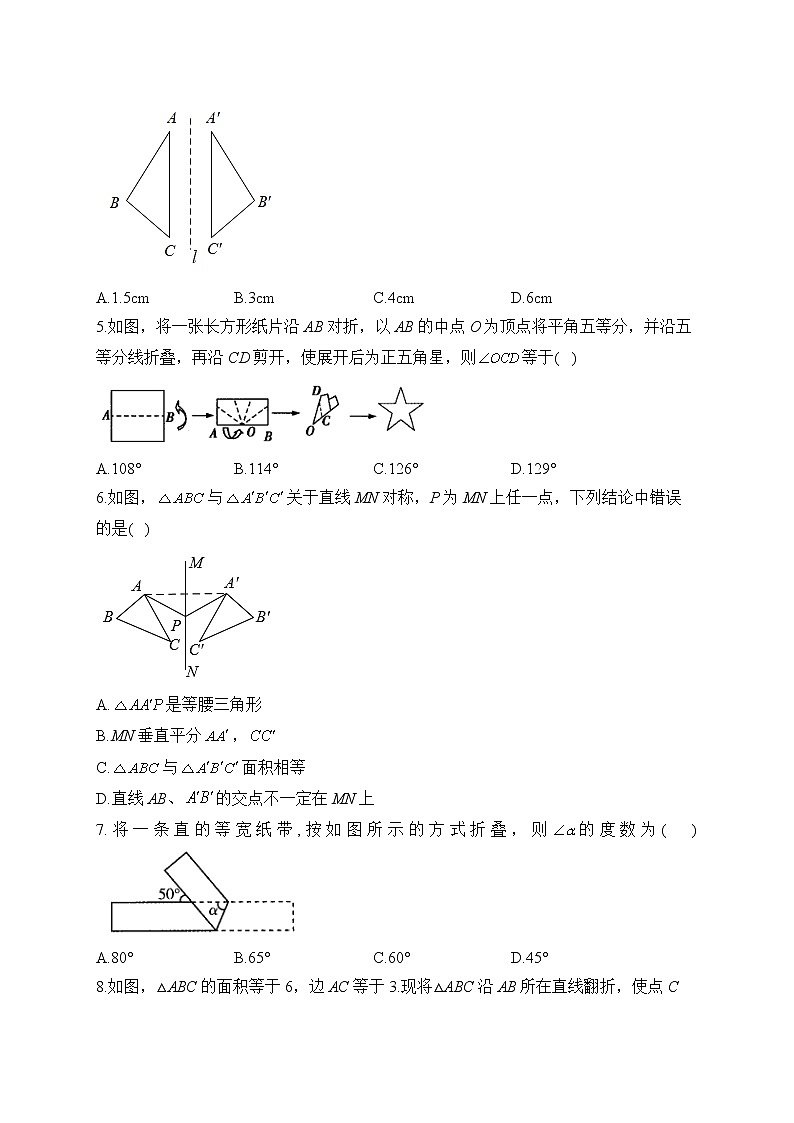
A.35° B.45 C.55° D.60°4.如图，与关于直线l对称，已知，的面积是，则边上的高是(   )A.1.5cm B.3cm C.4cm D.6cm5.如图，将一张长方形纸片沿AB对折，以AB的中点O为顶点将平角五等分，并沿五等分线折叠，再沿CD剪开，使展开后为正五角星，则等于(   )

A.108° B.114° C.126° D.129°6.如图，与关于直线MN对称，P为MN上任一点，下列结论中错误的是(   )A.是等腰三角形 B.MN垂直平分，C.与面积相等 D.直线AB、的交点不一定在MN上7.将一条直的等宽纸带,按如图所示的方式折叠，则的度数为(   )

A.80° B.65° C.60° D.45°8.如图，△ABC的面积等于6，边AC等于3.现将△ABC沿AB所在直线翻折，使点C落在直线AD上的C处，点P在直线AD上，则线段BP的长不可能是(   )

A.3 B.4 C.5 D.69.如图，在四边形ABCD中，，点B关于AC的对称点恰好落在CD上.若，则的度数为(   )

A.35° B.40° C.60° D.70°10.如图，在△ABC中，点D是边AB,AC的垂直平分线的交点，，则(   )

A.110° B.100° C.80° D.50°二、填空题（每小题4分，共20分）11.当写有数字的纸条垂直于镜面摆放时（如图所示）：

下面是从镜子中看到的一串数字，它其实是______________.12.如图，在中，，PQ垂直平分AB，垂足为Q，交BC于点P.按以下步骤作图：①以点A为圆心，以适当的长为半径作弧，分别交边AC，AB于点D，E；②分别以点D，E为圆心，以大于的长为半径作弧，两弧相交于点F；③作射线AF.若AF与PQ的夹角为，则________°.
 13.如图，将△ABC沿DE,EF分别翻折，顶点A,B均落在点O处，且EA与EB重合于线段EO,若，则的度数为_________.14.如图，点P为内任一点，E，F分别为点P关于直线OA，OB对称的点.若，则____________°.15.如图，在四边形ABCD中, ，点M,N分别是CD,BC上的两个动点，当△AMN的周长最小时，的度数为_________.
 三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）16.（8分）轴对称在数学计算中有巧妙应用.如图1，现要计算长方形中六个数字的和，我们发现，把长方形沿对称轴对折，重合的数字的和均为4，故六个数字的和为，若沿对称轴对折，则六个数字的和可表示为.受上面方法的启发，请快速计算正方形（图2）中所有数字之和.
 17.（8分）如图，点P是外的一点，点Q与点P关于OA对称，点R与点P关于OB对称，直线QR分别交OA,OB于点M,N.若，，求线段MQ,QN,QR的长.
 18.（10分）如图，点A,B在直线的同侧.

（1）试在直线上取一点M，使最小；
（2）试在直线上取一点N，使最大.19.（10分）如图，把三角形纸片ABC沿DE折叠，使点A落在四边形BCDE内部.

（1）写出图中一对全等的三角形，并写出它们所有的对应角；（2）设的度数为x，的度数为y，那么的度数分别是多少？（用含有x或y的代数式表示）（3）在（2）的条件下，请写出与之间的数量关系.20.（12分）回答下列问题：

（1）小明同学把三角形纸片ABC沿DE折叠，如图1所示，当点A落在四边形BCED的内部时，经过多次折叠他发现了，试说明其中的原因.
（2）如果把三角形纸片ABC沿DE折叠，如图2所示，当点A落在四边形BCED的外部时，与之间有一种数量关系也始终保持不变，请试找一找这个规律，你发现的规律和（1）中一样吗？21.（12分）如图，在△ABC中，于点F,于点M, cm, cm, cm，动点E以2 cm/s的速度从A点向F点运动，同时动点G以1 cm/s的速度从C点向A点运动，当一个点到达终点时，另一个点也随之停止运动，设运动时间为t s.

（1）求.
（2）试说明：在运动过程中，无论t取何值，都有.
（3）当t取何值时，△DFE与△DMG全等？
答案以及解析1.答案：C解析：A.这个图形是轴对称图形，故选项A不符合题意；B.这个图形是轴对称图形，故选项B不符合题意；C.这个图形不是轴对称图形，故选项C符合题意；D.这个图形是轴对称图形，故选项D不符合题意；故选：C.2.答案：C解析：如图所示：将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有4种.故选：C.3.答案：C解析：解法一  由题可知，△ABC是等腰三角形，AD是底边BC上的中线，所以，即，所以.故选C.
解法二  由题可知，△ABC是等腰三角形，AD是底边BC上的中线，所以，，所以.故选C.4.答案：B解析：与关于直线l对称，，的面积是，，的面积也是，边上的高为.故选B.5.答案：C解析：如图，正五角星每个角的度数都是，因为，所以.故选C.6.答案：D解析：由题意与关于直线MN对称，P为MN上任意一点，对称轴上的任何一点到两个对应点之间的距离相等，，是等腰三角形，选项A正确，不符合题意；轴对称图形对应点所连的线段被对称轴垂直平分，MN垂直平分，，选项B正确，不符合题意；轴对称图形对应的角、线段都相等，与是全等三角形，面积也必然相等，选项C选项正确，不符合题意；直线AB、关于直线MN对称，因此交点一定在MN上.选项D错误，符合题意.故选D.7.答案：B解析：如图，根据两直线平行，同位角相等，可知，由折叠可知，四边形ABCD与四边形BEFC关于直线BC对称，所以，所以.
 8.答案：A解析：如图，过点B作于点E，由翻折易知，，所以，所以，所以.因为于点E，点P在直线AD上，由垂线段最短可知，所以，故结合选项，知选A.
 9.答案：A解析：如图，连接，，过点A作于点E，因为点B关于AC的对称点B恰好落在CD上，所以AC垂直平分，所以，所以.因为，所以，又因为，所以，所以.因为，所以.故选A.
 10.答案：B解析：如图，连接AD，因为，所以.因为点D是边AB,AC的垂直平分线的交点，所以，所以，所以，所以，所以.故选B.
 11.答案：526778022解析：根据镜面对称的性质,知题中图片所显示的串数字与成轴对称,故纸条上的数字为526778022.12.答案：55解析：设AF与QP相交于点M.在中，，，所以，由作图易知AF是的平分线，所以，因为PQ是AB的垂直平分线，所以，所以，所以.13.答案：39°解析：因为将△ABC沿DE,EF翻折,所以,所以,所以.14.答案：150解析：如图，连接OP，E，F分别为点P关于直线OA，OB对称的点，，，，，，，又，，.15.答案：100°解析：如图,作点A关于BC的对称点A,关于CD的对称点,连接,分别交BC,CD于点M,N,此时△AMN的周长最小因为,所以.因为,所以,,所以.
 16.答案：如图,把正方形沿对折,重合数字之和均为10,故所有数字之和为.
 17.答案：因为点P,Q关于OA对称,
由轴对称的性质,易得,
因为,所以.
因为点P,R关于OB对称,
由轴对称的性质,易得,
所以.18.答案：(1)如图,作点A关于直线的对称点C,连接BC交直线于点M连接MA,此时,由两点之间线段最短知,此时最小,故点M即所求.

（2）如图，连接BA并延长，交直线于点N，此时，由三角形的三边关系知，此时最大，故点N即所求.19.答案：(1),其中与,与,与分别是对应角.
(2)，.
(3).因为，
所以.20.答案：（1）由题意可知，，.
因为点A落在四边形BCED的内部处，
所以，所以.
（2）如图，当点A落在四边形BCED的外部时，寻找的规律是，与1中的规律不一样.
因为△是△ADE沿DE折叠得到的，
所以，
易证.
因为.
所以.整理得，
即.
 21.答案：(1)因为,
所以.
因为,
所以.
(2)因为，
所以.
因为动点E以2 cm/s的速度从A点向F点运动,同时动点G以1 cm/s的速度从C点向A点运动,
所以 cm, cm,
所以,所以.
所以在运动过程中,无论t取何值,都有.
（3）在△ADF和△ADM中，
所以（AAS），所以 cm.
由题意知cm, cm，
所以.
①当点G在线段AM上时cm.
当时，△DFE与△DMG全等，
所以，解得.
②当点G在线段CM上时，cm，
当时，△DFE与△DMG全等，
所以，解得（舍去）.
综上，当时，△DFE与△DMG全等.