高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质教案配套课件ppt

这是一份高中数学人教A版 (2019)必修 第一册5.4 三角函数的图象与性质教案配套课件ppt，共43页。PPT课件主要包含了学习目标，自主探究，小试牛刀，经典例题，当堂达标，课堂小结等内容，欢迎下载使用。

1.了解正切函数的画法，理解并掌握正切函数的性质.2.能够利用正切函数的图象与性质解决相关问题.
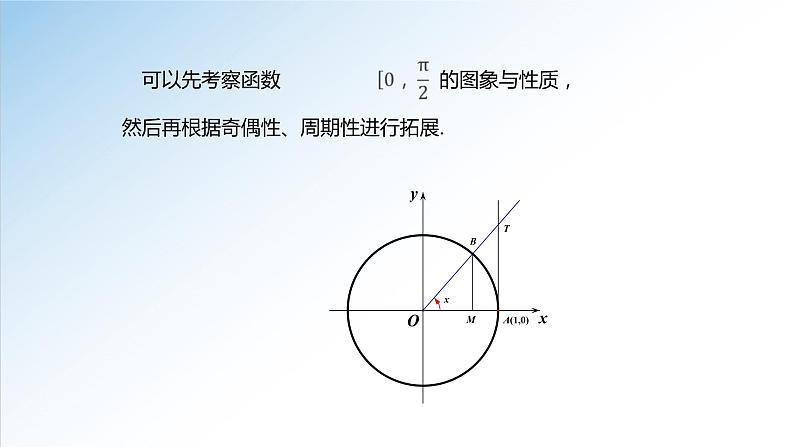
（1）根据研究正弦函数、余弦函数的经验，应如何研究正切函数？
有了前面的知识准备，我们可以换个角度，即从正切函数的定义出发研究它的性质，再利用性质研究正切函数的图象.
（2）你能用不同的方法研究正切函数吗？
设α是一个任意角，α∈R，它的终边OP与单位圆相较于点P(x,y).
可知，正切函数是周期函数，周期是π.
可知，正切函数是奇函数.
利用三角函数线得到正切函数的动态图象：
观察正切曲线可知，正切函数在区间 上单调递增.由正切函数的周期性可得，
正切函数在每一个区间 上都单调递增.
当 时，tan x在(-∞,+∞)内可取到任意实数值，但没有最大值、最小值，因此，正切函数的值域是实数集R.
答案　没有.正切曲线是由被互相平行的直线x＝kπ＋ (k∈Z)隔开的无穷多支曲线组成的.
1.正切函数的定义域和值域都是R.(　　)2.正切函数图象是中心对称图形，有无数个对称中心.(　　)3.正切函数图象有无数条对称轴，其对称轴是x＝kπ± ，k∈Z.(　　)4.正切函数是增函数.(　　)
题型一 正切函数的奇偶性与周期性
(2)函数f(x)＝sin x＋tan x的奇偶性为A.奇函数 B.偶函数C.非奇非偶函数 D.既是奇函数又是偶函数
关于原点对称，又f(－x)＝sin(－x)＋tan(－x)＝－sin x－tan x＝－f(x)，∴f(x)为奇函数.
总结：与正切函数有关的函数的周期性、奇偶性问题的解决策略(1)一般地，函数y＝Atan(ωx＋φ)的最小正周期为T＝ ，常常利用此公式来求周期.(2)判断函数的奇偶性要先求函数的定义域，判断其是否关于原点对称，若不对称，则该函数无奇偶性；若对称，再判断f(－x)与f(x)的关系.
A.是奇函数B.是偶函数C.既是奇函数又是偶函数D.既不是奇函数也不是偶函数
∴函数f(x)的定义域关于原点对称.
∴|ω|＝2，∴ω＝±2.
题型二 正切函数的单调性及其应用
(1)运用正切函数单调性比较大小的方法①运用函数的周期性或诱导公式将角化到同一单调区间内.②运用单调性比较大小关系.(2)求函数y＝tan(ωx＋φ)的单调区间的方法y＝tan(ωx＋φ)(ω>0)的单调区间的求法是把ωx＋φ看成一个整体，解－ ＋kπ<ωx＋φ< ＋kπ，k∈Z即可.当ω<0时，先用诱导公式把ω化为正值再求单调区间.
例3. （1）求函数 的定义域、周期及单调区间.
题型三 正切函数图象与性质的综合应用
由 解得
因此，函数在区间 上单调递增.
例3.（1） 求函数 的定义域、周期及单调区间.
解答正切函数图象与性质问题的注意点
1.(1)正切函数图象的画法.(2)正切函数的性质.2.方法归纳：整体代换、换元法.