



2020-2021学年18.2.1 矩形教案配套课件ppt
展开Urumqi N.47 middle schl –Liu Tngyan
问题1:工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和三角板),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
问题2:你还记得学习平行四边形的判定时,我们是如何猜想并进行证明的吗?
类比平行四边形的定义也是判定平行四边形的一种方法,那么矩形的定义也是判定矩形的一种方法.
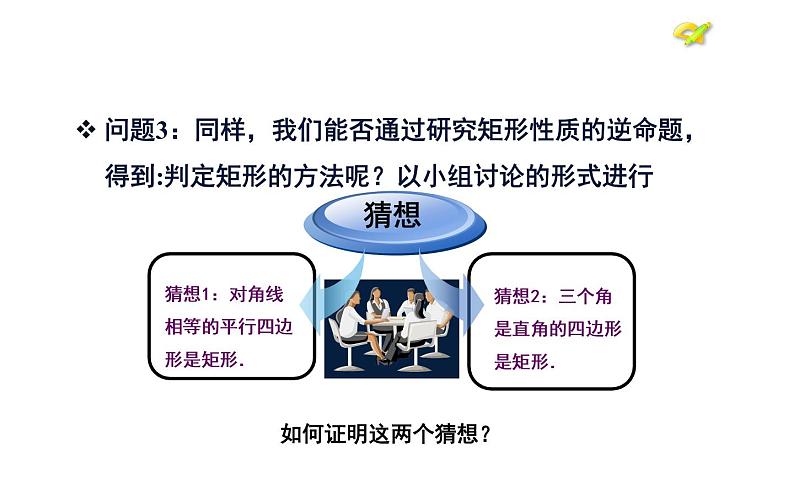
问题3:同样,我们能否通过研究矩形性质的逆命题,得到:判定矩形的方法呢?以小组讨论的形式进行
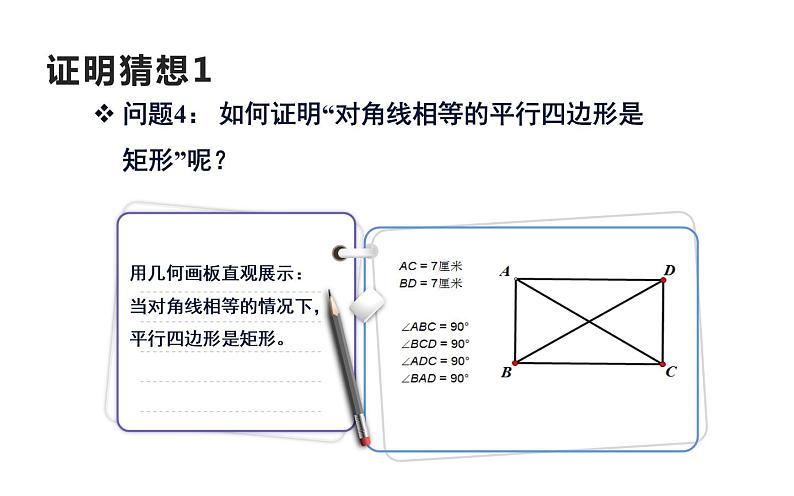
问题4: 如何证明“对角线相等的平行四边形是矩形”呢?
已知:如图,在□ABCD中,AC , DB是它的两条对角线, AC=DB.求证:□ABCD是矩形.证明:在平行四边形ABCD中,AB = DC,BC = AD, 又∵AC = DB, ∴ △ABC≌△DCB (SSS), ∴∠ABC = ∠DCB. ∵AB∥CD, ∴∠ABC + ∠DCB = 180°, ∴ ∠ABC = 90°, ∴ □ ABCD是矩形(矩形的定义).
矩形的判定定理1:对角线相等的平行四边形是矩形.
几何语言描述:∵在平行四边形ABCD中,AC=BD,∴平行四边形ABCD是矩形.
思考:对角线相等的四边形是矩形吗?如果不是,举出反例。
问题5:有四个角是直角的四边形是矩形吗?至少需要几个角是直角的四边形才是矩形?请同学们动手画画,得出猜想。
猜测:有三个角是直角的四边形是矩形
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°,∴AD∥BC,AB∥CD.∴四边形ABCD是平行四边形,又∵ ∠A=90°,∴四边形ABCD是矩形.
矩形的判定定理2:有三个角是直角的四边形是矩形.
几何语言描述:∵在四边形ABCD, ∠A=∠B=∠C=900∴四边形ABCD是矩形
1、判断下列说法是否正确?
例1:如图,在□ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=500.求∠OAB的度数。
证明:∵四边形ABCD是平行四边形 ∴OA=OC=1/2AC,OB=OD=1/2BD ∵OA=OD ∴AC=BD ∴平行四边形ABCD是矩形∴∠DAB=900又∠OAD=500∴∠OAB=400
1.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.求证:四边形ABCD是矩形.
证明:四边形ABCD中,AB∥CD,∠BAD=90°,∴∠ADC=90°.又∵△ABC中,AB=5,BC=12,AC=13,满足132=52+122,即∴△ABC是直角三角形,且∠B=90°,∴四边形ABCD是矩形.
2.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD是平行四边形?(2)经过多长时间,四边形PQBA是矩形?
解(1)设经过xs,四边形PQCD为平行四边形, 即PD=CQ, 所以24-x=3x, 解得x=6. 即经过6s,四边形PQCD 是平行四边形;
解:设经过ys,四边形PQBA为矩形,即AP=BQ,∴y=26-3y,解得y=6.5,即经过6.5s,四边形PQBA是矩形.
1、课本:习题18.2,第1题,第2题
2、同步练习册:18.2.1矩 形(第二课时)
初中数学人教版九年级下册29.1 投影教学ppt课件: 这是一份初中数学人教版九年级下册29.1 投影教学ppt课件,共50页。PPT课件主要包含了CONTENTS,照射光线叫做投影线,投影面,投影线,知识讲解,平行投影,中心投影,正投影,斜投影,线段小等内容,欢迎下载使用。
初中数学人教版九年级下册27.3 位似背景图ppt课件: 这是一份初中数学人教版九年级下册27.3 位似背景图ppt课件,共20页。PPT课件主要包含了位似图形的定义,位似多边形的定义,探究1,坐标表示等内容,欢迎下载使用。
人教版八年级下册19.2.2 一次函数评课ppt课件: 这是一份人教版八年级下册19.2.2 一次函数评课ppt课件,共20页。PPT课件主要包含了天气温度,高山气温,海拔高度,运动与变化,变量与常量,自变量与函数,单值对应,函数的定义,狄利克雷,判定函数的方法等内容,欢迎下载使用。













