数学选修1-23.1数系的扩充和复数的概念多媒体教学课件ppt

这是一份数学选修1-23.1数系的扩充和复数的概念多媒体教学课件ppt，共54页。PPT课件主要包含了直角坐标系，纯虚数等内容，欢迎下载使用。

主题一：复数的几何意义【自主认知】1.在什么条件下，复数z唯一确定？提示：给出复数z的实部和虚部.2.设复数z=a+bi(a，b∈R)，以z的实部和虚部组成一个有序实数对(a，b)，那么复数z与有序实数对(a，b)之间是一个怎样的对应关系？提示：一一对应关系.
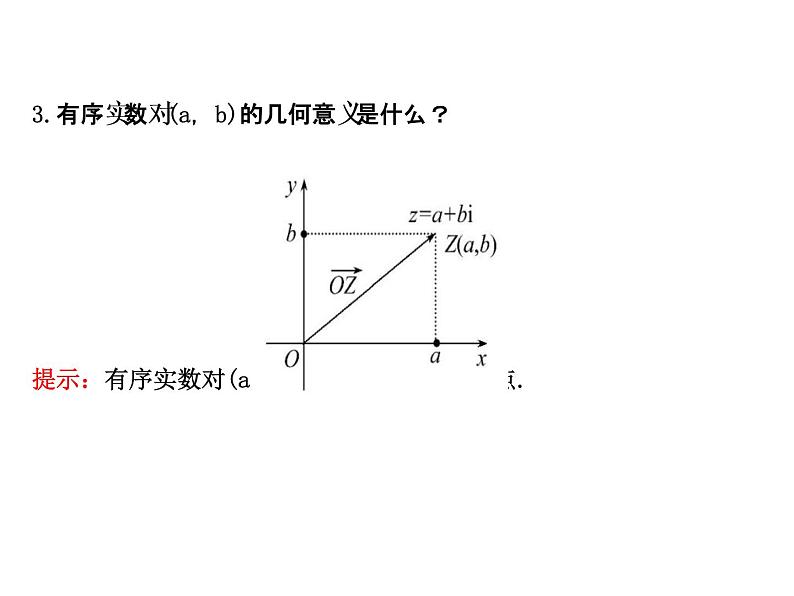
3.有序实数对(a，b)的几何意义是什么？提示：有序实数对(a，b)表示坐标平面内的点.
4.用有向线段表示平面向量，向量的大小和方向由什么要素所确定？提示：有向线段的始点和终点.5.在复平面内，复数z=a+bi(a，b∈R)用向量如何表示？提示：以原点O为始点，点Z(a，b)为终点的向量.
➡根据以上探究过程，试着写出复平面的概念以及复数与点、向量间的对应关系：1.复平面的概念(1)复平面：用___________来表示复数的平面.(2)____叫做实轴，____叫做虚轴.(3)实轴上的点都表示_____，虚轴上的点(除原点外)都表示_______.
2.复数与点、向量间的对应
【合作探究】1.复平面中，实轴上的点一定表示实数，虚轴上的点一定表示虚数吗？提示：在复平面中，实轴上的点一定表示实数，但虚轴上的点不一定表示虚数.事实上，虚轴上的点(0，0)是原点，它表示实数0，虚轴上的其他点都表示纯虚数.
2.用坐标表示平面向量，如何根据向量的坐标画出表示向量的有向线段？提示：以原点为始点，向量的坐标对应的点为终点画有向线段.3.复数与平面向量是什么关系？提示：一一对应关系
【拓展延伸】复数的三角形式(1)定义：复数z=a+bi(a，b∈R)表示成r(csθ+isinθ)的形式叫复数z的三角形式.即z=r(csθ+isinθ)，其中θ为复数z的辐角.(2)非零复数z辐角θ的多值性.以Ox轴正半轴为始边，向量所在的射线为终边的角θ叫复数z=a+bi的辐角，因此复数z的辐角是θ+2kπ(k∈Z).
(3)辐角主值表示法；用arg z表示复数z的辐角主值.①定义：适合[0，2π)的角θ叫辐角主值，②唯一性：复数z的辐角主值是确定的，唯一的.③z=0时，其辐角是任意的.
【过关小练】1.已知复数z=i，复平面内对应点Z的坐标为(　　)A.(0，1) B.(1，0)C.(0，0) D.(1，1)【解析】选A.复数z=i的实部为0，虚部为1，所以对应点的坐标为(0，1).
2.向量a=(1，-2)所对应的复数是(　　)A.z=1+2iB.z=1-2iC.z=-1+2iD.z=-2+i【解析】选B.因为a=(1，-2)，所以复平面内对应的点为Z(1，-2)，所以a对应的复数为z=1-2i.
主题二：复数的模【自主认知】1.设Z(a，b)，则向量 的模如何用a，b表示？提示：
2.根据复数模的意义，考虑|a+bi|的计算公式是什么？提示：|a+bi|=3.向量 的模r与复数z=a+bi的模|z|有何关系？提示：相等.即r=|z|=
➡根据以上探究过程，总结出复数模的定义以及计算公式：(1)复数z=a+bi(a，b∈R)模的定义：____________________________.(2)复数z=a+bi(a，b∈R)模的计算：___________________.
【合作探究】1.若|z|=1，|z|<1，则复数z对应复平面内的点的轨迹分别是什么？提示：单位圆，单位圆内部.2.两个复数的模能比较大小吗？提示：因为两复数的模是非负实数，因此能比较大小.
【过关小练】1.已知复数z=1-i，那么|z|等于(　　)A.0 B.1 C. D.2【解析】选C.|z|=|1-i|=
2.下面四个式子中，正确的是(　　)A.3i>2i B.|2+3i|>|1-4i|C.|2-i|>2i4 D.i2>-i【解析】选C.因为两个虚数不能比较大小，因此排除选项A和D.因为 所以|2+3i|<|1-4i|，选项B错误，因为|2-i|= ，2i4=2，所以|2-i|>2i4，选项C正确.
【归纳总结】1.复数的模的两个关注点(1)从几何意义上理解，复数的模表示点Z到原点的距离.(2)模的计算公式：|a+bi|= ，求复数的模，关键是明确复数的实部与虚部，将复数化为代数形式，然后根据公式求解.
2.复数z=a+bi(a，b∈R)、复平面上的点Z(a，b)与平面向量三者之间的联系与区别(1)联系：三者一一对应，是通过有序实数对在三者之间建立起一一对应关系.因此三者都表示复数z，为了方便起见，把复数z=a+bi(a，b∈R)说成点Z(a，b)或向量 .(2)区别：主要是表达形式不同.z=a+bi(a，b∈R)→从数的角度刻画复数，称为复数的代数形式.点Z(a，b)→从形的角度刻画复数，称为复数的几何形式.向量→从形的角度刻画复数，称为复数的向量形式.
类型一：复数与点的对应关系【典例1】(1)若θ∈ 则复数z=(sinθ-csθ)+(sinθ+csθ)i在复平面内所对应的点在(　　)A.第一象限 B.第二象限C.第三象限 D.第四象限
(2)求实数a分别取何值时，复数z= +(a2-2a-15)i(a∈R)对应的点Z满足下列条件：①在复平面的第二象限内.②在复平面内的x轴上方.【解题指南】(1)根据所给角θ的范围，确定复数z的实部与虚部的符号.(2)由z=a+bi(a，b∈R)与点Z(a，b)一一对应知第①问要求实部小于0，虚部大于0；第②问要求虚部大于0.
【解析】(1)选D.sin θ-cs θ=sin θ+cs θ= 因为因此sin θ-cs θ＞0，sin θ+cs θ＜0，所以复数z在复平面内对应的点在第四象限.
(2)①点Z在复平面的第二象限内，则 解得a＜-3.②点Z在x轴上方，则即(a+3)(a-5)＞0，解得a＞5或a＜-3.
【延伸探究】1.(改变问法)题(2)中题设条件不变，求复数z表示的点在x轴上时实数a的值.【解析】点Z在x轴上，所以a2-2a-15=0，所以a=5或a=-3.当a=-3时， 无意义，故a=5时，点Z在x轴上.
2.(改变问法)题(2)中条件不变，如果点Z在直线x+y+7=0上，如何求解？【解析】因为点Z在直线x+y+7=0上，所以 +a2-2a-15+7=0，即a3+2a2-15a-30=0，所以(a+2)(a2-15)=0，故a=-2或a=± .所以a=-2或a=± 时，点Z在直线x+y+7=0上.
【规律总结】复数与点的对应关系及应用(1)复平面内复数与点的对应关系的实质是：复数的实部就是该点的横坐标，虚部就是该点的纵坐标.(2)已知复数在复平面内对应的点满足的条件求参数的取值范围时，可根据复数与点的对应关系，建立复数的实部与虚部满足的条件构成的方程(组)或不等式(组)，通过解方程(组)或不等式(组)得出结论.
【补偿训练】当实数m分别为何值时，复数(m2-8m+15)+(m2+3m-28)i在复平面内对应的点：(1)位于第四象限？(2)位于x轴的负半轴上？(3)位于y轴的正半轴上？【解题指南】复数a+bi(a，b∈R)在复平面内对应的点位于第四象限应满足a>0且b<0；位于x轴的负半轴上应满足a<0且b=0；位于y轴的正半轴上，应满足a=0且b>0.
【解析】(1)当复数(m2-8m+15)+(m2+3m-28)i在复平面内对应的点位于第四象限时，所以-7(2)当复数(m2-8m+15)+(m2+3m-28)i在复平面内对应的点位于x轴的负半轴上时，有故当m=4时，该复数在复平面内对应的点位于x轴的负半轴上.
(3)当复数(m2-8m+15)+(m2+3m-28)i在复平面内对应的点位于y轴的正半轴上时，有故当m=5时，该复数在复平面内对应的点位于y轴的正半轴上.
类型二：复数与向量的对应【典例2】(1)已知复数z1=-3+4i，z2=2a+i(a∈R)对应的点分别为Z1和Z2，且 ，则a的值为.(2)已知向量 对应的复数是4+3i，点A关于实轴的对称点为A1，将向量 平移，使其起点移动到A点，这时终点为A2.①求向量 对应的复数.②求点A2对应的复数.
【解题指南】(1)利用复数与向量的对应关系，转化为向量的数量积求解.(2)根据复数与点、复数与向量的对应关系求解.【解析】(1)依题意可知 =(-3，4)， =(2a，1)，因为即-6a+4=0，解得a= .答案：
(2)①因为向量 对应的复数是4+3i，所以点A对应的复数也是4+3i，因此点A坐标为(4，3)，所以点A关于实轴的对称点A1为(4，-3)，故向量 对应的复数是4-3i.②依题意知 =(4，-3)，设A2(x，y)，则有(4，-3)=(x-4，y-3)，所以x=8，y=0，即A2(8，0).所以点A2对应的复数是8.
【延伸探究】若将题(2)中条件作如下改动：向量 对应的复数为-5+3i，将向量 向下平移1个单位，向右平移2个单位得到向量 ，如何求①向量 对应的复数？②点A1对应的复数？
【解析】如图，由于O为原点， 对应的复数为-5+3i，所以A点坐标为(-5，3)，向量 向下平移1个单位，向右平移2个单位后，点O1的坐标为(2，-1)，点A1的坐标为(-3，2).①向量 对应的复数与 对应的复数相同，仍为-5+3i.②点A1对应的复数为-3+2i.
【规律总结】复数与向量的对应关系的两个关注点(1)复数z=a+bi(a，b∈R)是与以原点为起点，Z(a，b)为终点的向量 一一对应的.(2)一个向量可以平移，其对应的复数不变，但是其起点与终点所对应的复数可能改变.
【巩固训练】已知平行四边形OABC中，O，A，C三点对应的复数分别为0，1+2i，3-2i，求向量 的模.【解题指南】根据平行四边形的特征，利用向量相等可求解.【解析】由于四边形OABC是平行四边形，所以因此
【补偿训练】已知ABCD是复平面内一个平行四边形， 对应的复数为1+i， 对应的复数为3-2i，其中i为虚数单位，则 对应的复数为( )A.2-3i B.-2+3i C.4-i D.-4+i【解析】选C.因为ABCD是复平面内一个平行四边形， 对应的复数为1+i， 对应的复数为3-2i，根据平行四边形法则得到 =(1+i)+(3-2i)=4-i，所以 对应的复数是4-i.
类型三：复数的模【典例3】(1)(2015·重庆高二检测)若复数z对应的点在直线y=2x上，且|z|= ，则复数z=(　　)A.1+2i B.-1-2i C.±1±2iD.1+2i或-1-2i(2)(2015·杭州高二检测)设复数z1=a+2i，z2=-2+i，且|z1|<|z2|，则实数a的取值范围是(　　)A.a<-1或a>1 B.-11 D.a>0
【解题指南】(1)设z=a+2ai(a∈R)，由复数模的计算公式列方程求出a值即可.(2)根据复数模的计算公式列不等式得出答案.
【解析】(1)选D.依题意可设复数z=a+2ai(a∈R)，由|z|= 得 解得a=±1，故z=1+2i或z=-1-2i.(2)选B.因为 所以 即a2+4<5，所以a2<1，即-1【规律总结】复数模的计算(1)计算复数的模时，应先确定复数的实部和虚部，再利用模长公式计算.虽然两个虚数不能比较大小，但它们的模可以比较大小.(2)设出复数的代数形式，利用模的定义转化为实数问题求解.提醒：复数的模表示该复数在复平面内的对应点到原点的距离，则任何一个复数的模都是非负数.
【拓展延伸】求解关于复数模的最值问题的两种方法(1)设z=x+yi(x，y∈R)直接代入所要求的式子中去，把所要求的模用x，y的函数表示出来，转化为函数最值问题.(2)因为复数和图形有着密切的关系，可以利用这种关系把所给条件转化为图形，直观地求出最大值、最小值.
【巩固训练】1.如果复数z=1+ai满足条件|z|<2，那么实数a的取值范围是(　　)A.(-2 ，2 ) B.(-2，2)C.(-1，1) D.(- ， )【解析】选D.因为|z|<2，所以 <2，则1+a2<4，a2<3，解得- 2.(2015·济南高二检测)设复数z满足z+|z|=2+i，那么z等于( )A.- +i B. -i C.- -i D. +i【解析】选D.设z=a+bi(a，b∈R)，则a+bi+ =2+i.解得a= ，b=1.所以z= +i，故选D.
【补偿训练】求复数z1=3+4i及z2= 的模，并比较它们的模的大小.【解析】因为z1=3+4i，z2=所以|z1|= =5，|z2|=因为5＞ ，所以|z1|＞|z2|.
拓展类型：复数在复平面内对应点的轨迹【典例】1.已知复数z满足|z|2-2|z|-3=0，则复数z对应的点Z的轨迹是(　　)A.2个点B.1个圆C.2个圆D.1条线段
2.已知复数z1=x-2+yi(x，y∈R)的模是2 ，则复数z2=x+yi对应点的轨迹方程是　　　　.3.已知a∈R，问复数z=(a2-2a+4)-(a2-2a+2)i所对应的点在第几象限？复数z对应的点的轨迹是什么？
【解题指南】1.先解出|z|，再根据复数的模的几何意义判断.2.根据复数模的计算公式，把已知转化为x，y的方程即得答案.3.先用配方法判断复数z的实部与虚部的符号得出其对应点所在象限，再设z=x+yi(x，y∈R)，利用复数相等的重要条件，然后消去参数a得到轨迹方程.
【解析】1.选B.由|z|2-2|z|-3=0，得(|z|+1)(|z|-3)=0，因为|z|+1>0，所以|z|-3=0，即|z|=3，它表示复数z对应的点到原点的距离为3，即其轨迹是以原点为圆心，以3为半径的圆.2.因为(2 )2=(x-2)2+y2，所以z2=x+yi所对应的点(x，y)的轨迹是以(2，0)为圆心，以2为半径的圆.答案：(x-2)2+y2=8
3.由a2-2a+4=(a-1)2+3≥3，-(a2-2a+2)=-(a-1)2-1≤-1.得z的实部为正数，虚部为负数.所以复数z的对应点在第四象限.设z=x+yi(x，y∈R)，则消去a2-2a得y=-x+2(x≥3)，所以复数z对应点的轨迹是一条射线，其方程为y=-x+2(x≥3).
【规律总结】解复数所对应点的图形问题常用两种方法方法一：根据|z|表示点Z和原点间的距离，直接判定图形形状.方法二：利用模的定义，把复数问题转化为实数问题来解决，这也是本章的一种重要思想方法.