初中24.2.2 直线和圆的位置关系精品课件ppt

这是一份初中24.2.2 直线和圆的位置关系精品课件ppt，共31页。PPT课件主要包含了知识回顾，切线的判定定理，切线的性质定理，学习目标，课堂导入，知识点1，新知探究，PB是☉O的切线吗，PAPB有何关系，同理可得OB⊥PB等内容，欢迎下载使用。

经过半径的外端并且垂直于这条半径的直线是圆的切线.
圆的切线垂直于过切点的半径.
1.掌握切线长的定义及切线长定理.
2.初步学会运用切线长定理进行计算与证明.
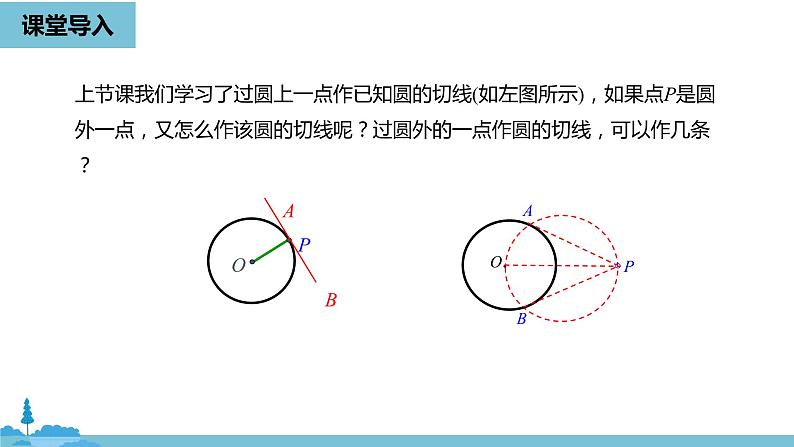
上节课我们学习了过圆上一点作已知圆的切线(如左图所示)，如果点P是圆外一点，又怎么作该圆的切线呢？过圆外的一点作圆的切线，可以作几条？
切线上一点到切点之间的线段的长叫作这点到圆的切线长．
①切线是直线，不能度量.
②切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量．
切线长与切线的区别在哪里？
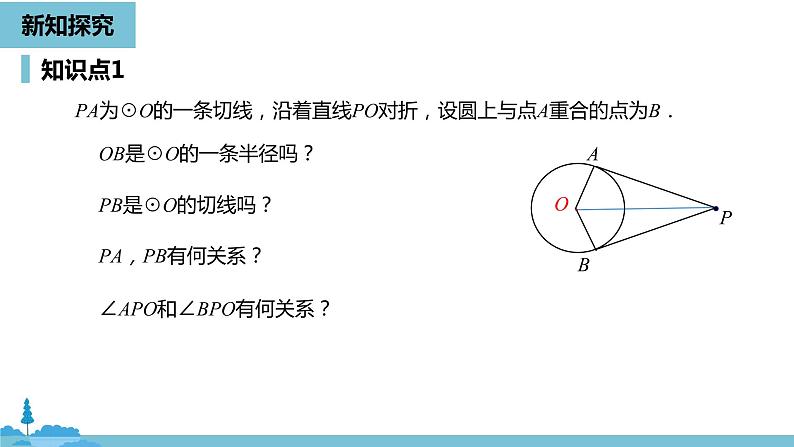
PA为☉O的一条切线，沿着直线PO对折，设圆上与点A重合的点为B．
OB是☉O的一条半径吗？
∠APO和∠BPO有何关系？
已知，如图PA ， PB是☉O的两条切线，A,B为切点.求证：PA=PB，∠APO=∠BPO.
证明：∵PA切☉O于点A，∴ OA⊥PA.
∵OA=OB，OP=OP，
∴Rt△OAP ≌ Rt△OBP，
∴PA=PB，∠APO=∠BPO.
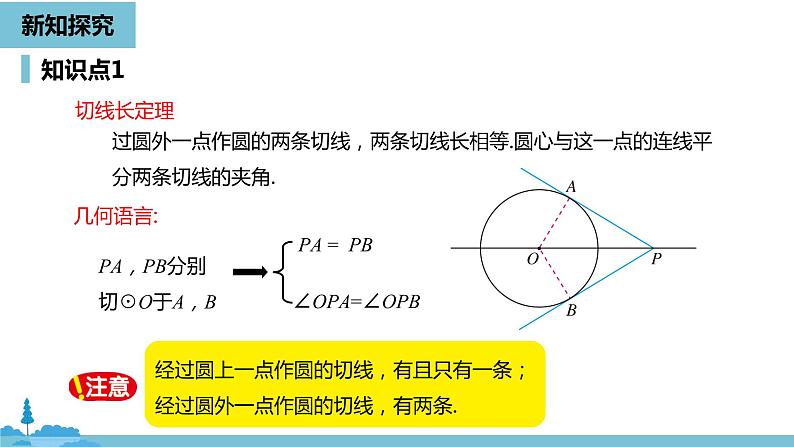
PA，PB分别切☉O于A，B
过圆外一点作圆的两条切线，两条切线长相等.圆心与这一点的连线平分两条切线的夹角.
若连接两切点A,B，AB交OP于点M.你又能得出什么新的结论？并给出证明.
证明：∵PA，PB是⊙O的切线，点A，B是切点，∴PA = PB ，∠OPA=∠OPB，∴△PAB是等腰三角形，PM为顶角的平分线，∴OP垂直平分AB.
若延长PO交⊙O于点C，连接CA,CB，你又能得出什么新的结论？并给出证明.
证明：∵PA，PB是⊙O的切线，点A，B是切点，∴PA = PB ，∠OPA=∠OPB.∴PC=PC.∴ △PCA ≌ △PCB， ∴AC=BC.
活学巧记过圆外一点作切线，此点与切点间线段长，名称就叫切线长.圆外一点引两切，牢记切线长相等，此点圆心两相连，平分两切之夹角.
如图，已知四边形ABCD的每条边都和⊙O相切，且BC= 10，AD = 7，则四边形ABCD的周长为( )
A.32B.34C.36D.38
解：设四边形的各边与圆的切点分别为P，Q，M，N，则AQ=AM，BN=BM，CN=CP，DP=DQ.所以四边形ABCD的两组对边的和相等，所以四边形ABCD的周长=2×(7+10)=34．
小明在一家木料厂上班，工作之余想对厂里的三角形废料进行加工：裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？
如果最大圆存在，它与三角形三边应有怎样的位置关系？
最大的圆与三角形三边都相切.
1.与三角形三边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
如何作一个圆，使它与已知三角形的三边都相切？
(1) 如果半径为r的☉O与△ABC的三边都相切，那么圆心 O 应满足什么条件？
(2) 在△ABC的内部，如何找到满足条件的圆心O呢？
圆心O到三角形三边的距离相等，都等于r.
三角形三条角平分线交于一点，这一点与三角形的三边距离相等.圆心O 应是三角形的三条角平分线的交点.
已知：△ABC.求作：和△ABC的各边都相切的圆.
作法：1.作∠B和∠C的平分线BM和CN，交点为O.2.过点O作OD⊥BC.垂足为D.3.以O为圆心，OD为半径作圆O.
作三角形任意两个内角的平分线，以两条角平分线的交点为圆心，以交点到三角形任意一边的距离为半径作圆即可.
如图，☉I是△ABC的内切圆，那么线段IA，IB，IC有什么特点？
线段IA，IB ，IC 分别是∠A，∠B，∠C 的平分线.
如图，分别过点 I 作AB，AC，BC的垂线，垂足分别为E，F，G，那么线段IE，IF，IG之间有什么关系？
三角形的内心到三角形的三边距离相等，且等于其内切圆的半径.
三角形外心、内心的区别
（2018·湖州中考）如图，已知△ABC的内切圆☉O与BC边相切于点D，连接OB，OD.若∠ABC=40°，则∠BOD的度数是 .
A.△ACD的外心B.△ABC的外心C.△ACD的内心D.△ABC的内心
如图为4×4的网格，A,B,C,D,O均在格点上，则点O是( )
如图，PA, PB, DE分别切☉O于点A,B,C,点D在PA上，点E在PB上.(1) 若PA=10，求△PDE的周长；(2) 若∠P=50°，求∠DOE的度数.
解：(1) 因为PA,PB,DE分别切☉O于点A,B,C, 所以PA=PB，DA=DC， EC=EB，所以PD+DE+PE=PD+DA+EB+PE=PA+PB=10+10=20，所以△PDE的周长为20.
提供了证线段和角相等的新方法
分别连接圆心和切点；连接两切点；连接圆心和圆外一点.
运用切线长定理，将相等线段转化集中到某条边上，从而建立方程.
（2020∙镇江模拟）如图，已知平面直角坐标系内三点A(3,0),B(5,0),C(0,4)， ☉P经过点A,B,C,则点P的坐标为( )
如图，☉O与正方形ABCD的两边AB, AD相切，且DE与☉O相切于点E.若☉O的半径为5,AB =11，则DE的长度为( )
解：连接OM，ON，∵四边形ABCD是正方形，∴AD=AB=11，∠A=90°，∵圆O与正方形ABCD的两边AB，AD相切，∴∠OMA=∠ONA=90°=∠A，∵OM=ON，∴四边形ANOM是正方形，∴AM=OM=5，∵AD和DE与圆O相切，圆O的半径为5，∴AM=5，DM=DE，∴DE=11-5=6.