

初中数学人教版九年级上册24.2.2 直线和圆的位置关系优质第1课时学案
展开24.2.2 直线和圆的位置关系学案
【学习目标】
1.使学生理解直线和圆的位置关系,掌握直线和圆的位置关系的数量关系定理及其运用.
2.掌握切线的性质、判定及其应用.
【重点难点】
重点:使学生正确理解直线和圆的位置关系,掌握切线的判定定理及其性质定理.
难点:直线和圆的位置关系与圆心到直线的距离和圆的关径大小关系的对应,它既可做为各种位置关系的判定,又可作为性质,学生不太容易理解.切线的判定定理及其性质定理的灵活应用.
【课堂探究】
一、自主探究
问题一
1、在纸上画一个圆,上下移动直尺画直线,观察并回答问题:
(1)直线与圆的公共点有何变化?
(2)在移动过程中,直线与圆有什么样的位置关系?
(3)圆心到直线的距离有什么变化?你能根据圆心到直线的距离的不同判断直线与圆有什么样的位置关系吗?
问题二
1、操作实践:
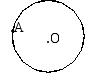 (1)根据直线与圆相切的定义,过点A用直尺近似地画出⊙O的切线.
(1)根据直线与圆相切的定义,过点A用直尺近似地画出⊙O的切线.
(2)圆的直径是13cm,如果直线与圆心的距离分别是①4.5cm②6.5cm③8cm,那么直线和圆分别是什么位置关系?有几个公共点?
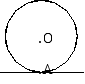 2、思考:如图在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线的距离是多少?直线l和⊙O有什么位置关系?
2、思考:如图在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线的距离是多少?直线l和⊙O有什么位置关系?
3、思考:将第2题反过来,如果直线l是⊙O的切线,切点为A,那么半径OA与直线l是不是一定垂直呢?
二、尝试运用
1、已知圆的直径为12cm,如果直线和圆心的距离为 ⑴ 5.5cm; ⑵ 6cm; ⑶ 8cm 那么直线和圆有几个公共点?为什么?
2、已知圆的直径为13cm,圆心到直线ι的距离为6cm,那么直线ι和这个圆的公共点的个数是 .
3. 已知⊙O的直径为6,P为直线ι上一点,OP=3,那么直线与⊙O的位置关系是__________.
4、在![]() 中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何位置关系?为什么?(1)r=2cm;(2)r=2.4cm;(3)r=3cm.
中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有何位置关系?为什么?(1)r=2cm;(2)r=2.4cm;(3)r=3cm.
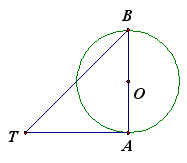
5、如图,AB是⊙O的直径,∠ABT=45°,AT=BT.求证:AT是⊙O的切线.
三、补偿提高
1、已知Rt△ABC的斜边AB=8,AC=4,以点C为圆心作圆,当半径R=_____时,AB与⊙C相切.
2、已知OA平分∠BOC,P为OA上任意一点,如果以P为圆心的圆与OC相离,那么⊙P与OB的位置关系是( )
A. 相离 B. 相切 C. 相交 D. 不能确定
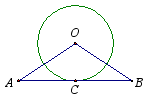
3、如图,直线AB经过⊙O上的一点C,并且AO=BO.求证:直线AB是⊙O的切线.
4、东海某小岛上有一灯塔A,已知A塔附近方圆25海里范围内有暗礁,我110舰在O点处测得A塔在其北偏西60°方向,向正西方向航行20海里到达B处,测得A在其西北方向.如果该舰继续航行,是否有触礁的危险?请说明理由.(提示![]() =1.414,
=1.414,![]() =1.732)
=1.732)
四、小结与作业
学生小结:
1.必做题
教材习题24.2P101第2题, P102第12题
2、 选做题
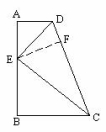
如图,直角梯形ABCD中,∠A=∠B=90°,AD//BC,E为AB上一点,DE平分∠ADC,CE平分∠BCD,以AB为直径的圆与边DC有怎样的位置关系?为什么?(提示:过E作EF⊥CD于F,证点E是以AB为直径的圆的圆心)
初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系学案设计: 这是一份初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系学案设计,共6页。学案主要包含了旧知回顾,新知梳理,试一试,拓展延伸等内容,欢迎下载使用。
人教版九年级上册24.2.2 直线和圆的位置关系学案: 这是一份人教版九年级上册24.2.2 直线和圆的位置关系学案,共6页。学案主要包含了巩固训练,错题再现,能力提升,精练反馈等内容,欢迎下载使用。
人教版九年级上册24.2.2 直线和圆的位置关系学案及答案: 这是一份人教版九年级上册24.2.2 直线和圆的位置关系学案及答案,共5页。学案主要包含了课时安排,新知探究,精练反馈,学习小结,拓展延伸等内容,欢迎下载使用。













