

初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系优秀第2课时导学案
展开24.2.2 直线和圆的位置关系学案
【学习目标】
1.掌握切线的判定定理.
2.应用切线的判定定理证明直线是圆的切线,初步掌握圆的切线证明问题中辅助线的添加方法.
3.培养学生动手操作能力.
4.培养学生观察、探索、分析、总结、推理论证等能力.
【重点难点】
教学重点:
切线的判定定理和切线判定的方法;
教学难点:
切线判定定理中所阐述的由位置来判定直线是圆的切线的两大要素:一是经过半径外端;二是直线垂直于这条半径;学生开始时掌握不好并极容易忽视.
【课堂探究】
回顾与思考
1.直线和圆有哪三种位置关系?这三种位置关系是如何定义?如何判定的?
2.什么叫做圆的切线?根据这个定义我们可以怎样来判定一条直线是不是一个圆的切线?
一、自主探究
问题一
1.切线判定定理的导出
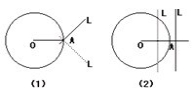
先画⊙O,在⊙O上任取一点A,边结OA,过A点作⊙O的切线L.
请学生回顾作图过程,切线L是如何作出来的?它满足哪些条件?
引导学生总结出:①经过关径外端,②垂直于这条半径.
2.请同学们思考一下,该判定定理的两个条件缺少一个可以吗?
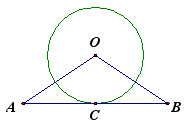
3.已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证 :直线AB是⊙O的切线.

二、尝试应用
1:已知:⊙O的直径长6cm,OA=OB=5cm,AB=8cm.
求证:AB与⊙O相切.
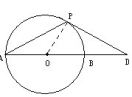
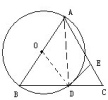
2、如图D是⊙O的直径AB延长线上一点,PD是⊙O的切线,P是切点,∠D=30°。求证:PA=PD.
3小结与反思
三、补偿提高
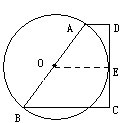
1、梯形ABCD中,AD∥BC,∠C=90°,且AD+BC=AB,AB为⊙O的直径
求证:⊙O与CD相切。
2、已知:在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D点作⊙O的切线交AC于E求证:(1)DE⊥AC;(2)BD2=CE·CA.
3、在直角坐标系中,⊙M的圆心坐标为(m,0),半径是2,如果⊙M与y轴所在的直线相切,那m等于______,若⊙M与y轴所在的直线相交,那么m的取值范围是__________。
四、小结与作业小结:
通过本节课的学习.你有那些收获?
作业:
课本P98 1.2
P101习题24.2 第3、5题
初中数学人教版九年级上册24.2.2 直线和圆的位置关系学案设计: 这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系学案设计,共7页。学案主要包含了旧知回顾,新知梳理,试一试,拓展延伸等内容,欢迎下载使用。
初中数学人教版九年级上册24.2.2 直线和圆的位置关系学案设计: 这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系学案设计,共5页。学案主要包含了课时安排,第二课时,学习目标,学习重难点,学习过程,达标检测,拓展创新等内容,欢迎下载使用。
初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系学案设计: 这是一份初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系学案设计,共6页。学案主要包含了旧知回顾,新知梳理,试一试,拓展延伸等内容,欢迎下载使用。













