初中数学人教版九年级上册24.2.2 直线和圆的位置关系优秀课件ppt

这是一份初中数学人教版九年级上册24.2.2 直线和圆的位置关系优秀课件ppt，文件包含人教版初中数学九年级上册24223切线长定理课件PPTpptx、人教版初中数学九年级上册24223切线长定理教案docx、人教版初中数学九年级上册24223切线长定理分层练习docx、人教版初中数学九年级上册24223切线长定理预习案docx等4份课件配套教学资源，其中PPT共33页， 欢迎下载使用。

人教版数学九年级上册
第二十四章 圆
24.2.2.3 切线长定理
理解切线长的概念.
掌握切线长定理,能用切线长定理进行有关计算和证明.
理解三角形的内切圆和三角形的内心的概念
1.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.2.切线的性质定理:圆的切线垂直于过切点的半径.
3.过圆外一点可以做几条切线，它们之间有什么关系？
1.切线长定理⑴切线长的定义:经过圆外一点的圆的切线上，这点和切点之间线段的长，叫作这点到圆的切线长.如图中的线段PA、PB.⑵切线长定理:从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.
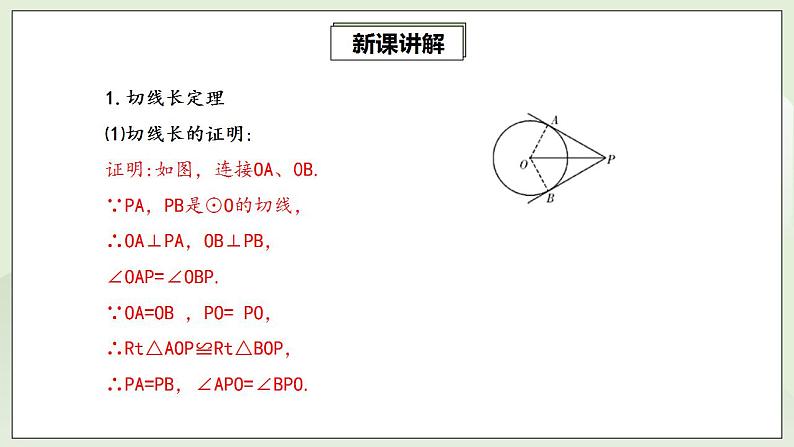
1.切线长定理⑴切线长的证明:证明:如图，连接OA、0B. ∵PA，PB是⊙O的切线，∴OA⊥PA，OB⊥PB，∠OAP=∠OBP.∵OA=OB ，PO= PO，∴Rt△AOP≌Rt△BOP，∴PA=PB，∠APO=∠BPO.
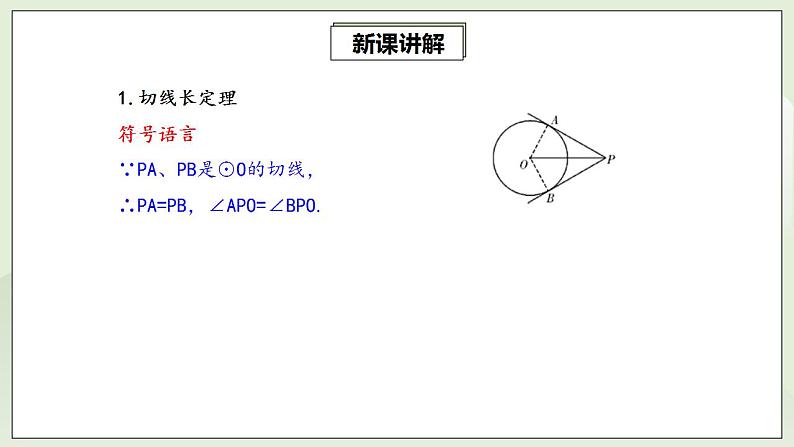
1.切线长定理符号语言∵PA、PB是⊙O的切线，∴PA=PB，∠APO=∠BPO.
 
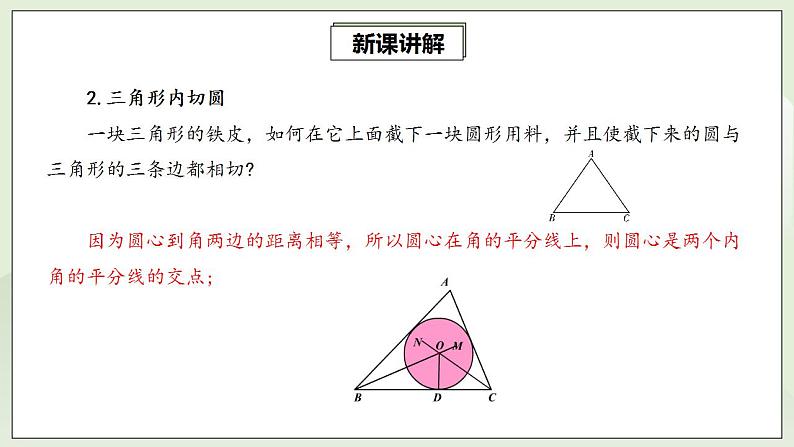
2.三角形内切圆一块三角形的铁皮，如何在它上面截下一块圆形用料，并且使截下来的圆与三角形的三条边都相切?因为圆心到角两边的距离相等，所以圆心在角的平分线上，则圆心是两个内角的平分线的交点;
三角形的外心与内心有什么区别？⑴概念外心(三角形的外接圆圆心，即三角形三边垂直平分线的交点).内心(三角形的内切圆圆心，即三角形三条角平分线的交点).⑵性质三角形的外心到三角形三个顶点的距离相等.三角形的内心到三角形三边的距离相等.⑶位置外心不一定在三角形的内部，内心一定在三角形的内部.
1.切线长定理的有关计算例1如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB=9， BC= 14，CA=13，求AF、BD、 CE的长. 解:设AF=x，则AE=x， CD=CE=AC-AE= 13-x，BD=BF=AB-AF=9-x.由BD+CD=BC，可得(9-x)+( 13-x)= 14.解得x=4.因此AF=4，BD=5，CE=9.
如图， P是⊙O外一点PA、PB分别和相⊙O切于点A、B， C是劣弧AB上任意一点， 过C作⊙O切线DE，交PA、PB于点D、E，已知∆ PDE的周长为8cm， ∠DOE = 70°.(1)求∠P的度数;(2)求PA的长.解: (1)连接OA、OB，如图. ∵PA、PB、DE分别和0O相切于点A、B、C，∴∠ADO=∠CDO，∠CEO=∠BEO，∠OAD=∠OCD=∠OCE=∠OBE= 90°，∴∠AOD=∠COD，∠COE=∠BOE，∴∠AOB= 2∠DOE=2×70°= 140°，∴∠P= 360°-∠OAP-∠OBP-∠AOB = 40°.∴PA的长为4cm.
如图， P是⊙O外一点PA、PB分别和相⊙O切于点A、B， C是劣弧AB上任意一点， 过C作⊙O切线DE，交PA、PB于点D、E，已知∆ PDE的周长为8cm， ∠DOE = 70°.(1)求∠P的度数;(2)求PA的长.(2) ∵PA、PB、DE分别和⊙O相切于点A、B、C，∴DA= DC， EC= EB， PA= PB，∴C∆ PDE= PD+ DE+ PE= PD+ DC+CE+ PE= PD+ DA+ BE+ PE= PA + PB= 2PA，∵C∆ PDE=8， PA= 4，∴PA的长为4cm.
2. 切线长定理的证明例2如图，PA，PB是⊙O的切线，切点分别为A、B，BC为⊙O的直径，连接AB、AC、OP.求证：（1）∠APB=2∠ABC；（2）AC∥OP. 证明：（1）如图：连接AO，∵PA，PB是⊙O的切线，切点分别为A，B，∴∠APO=∠BPO，OA⊥AP，PA=PB，∴∠APB=2∠APO，∠OAP=90°，PO⊥AB，∴∠OAB+∠BAP=90°，∠BAP+∠APO=90°，∴∠OAB=∠APO.∵OA=OB，∴∠OBA=∠OAB，∴∠OBA=∠APO，∴∠APB=2∠ABC.
2. 切线长定理的证明例2如图，PA，PB是⊙O的切线，切点分别为A、B，BC为⊙O的直径，连接AB、AC、OP.求证：（1）∠APB=2∠ABC；（2）AC∥OP. 证明：（2）设AB交OP于F，∵BC为⊙O的直径，∴∠CAB=90°.又∵PO⊥AB，∴∠CAB=∠AFP=90°，∴AC∥OP.
如图，AB是⊙O的直径，AD、BC、CD是⊙O的切线，切点分别是A、B、E；DO、AE相交于点F，CO、BE相交于点G.求证：(1)CO⊥DO；(2)四边形EFOG是矩形. 解：(1).连接OE，由已知可得OE⊥CD三角形OAD与EOD全等，三角形BOC与EOC全等那么∠AOD=∠EOD,∠EOC=∠BOC所以∠DOC=∠EOD+∠EOC=180°/2=90°所以CO⊥OD
如图，AB是⊙O的直径，AD、BC、CD是⊙O的切线，切点分别是A、B、E；DO、AE相交于点F，CO、BE相交于点G.求证：(1)CO⊥DO；(2)四边形EFOG是矩形. 解： (2)∵AB是⊙O的直径∴∠AEB=90°;由(1)可知CO⊥OD∴∠FOC=90°;∵三角形OAD与EOD全等，三角形BOC与EOC全等∵AD=DE,CE=BC;∴∠FDA=∠FDE;∠CBE=∠CBF∴DO⊥AE∴四边形EFOG是矩形.
 
 
1.如图，PA切⊙O于点A，PB切⊙O于点B，OP交⊙O于点C，下列结论错误的是( ).A.∠APO=∠BPO B. PA=PB C.AB⊥OP D.C是PO的中点分析: ∵PA，PB是⊙O的切线，切点分别是A、B， ∴PA=PB，∠BPO=∠APO， OP⊥AB，.选项A，B，C均不符合题意;根据已知不能得出C是PO的中点，故选项D符合题意.故选D.
D
2.下列命题正确的有( ).①三角形的内心到三角形各顶点的距离相等;②三角形的外心到三角形三边的距离相等;③等边三角形的内心和外心重合;④三角形的内心到三角形三边的距离相等. A.1个 B.2个 C.3个 D.4个分析:三角形的内心到三角形三边的距离相等;三角形的外心到三角形三个顶点的距离相等;等边三角形三条角平分线的交点与三边垂直平分线的交点重合，故①②错误，③④正确.故选B.
B
 
B
 
C
5.如图，在△ABC中，点P是△ABC的内心，则∠PBC+∠PCA+∠PAB=____°.分析:点P是△ABC的内心，PB平分∠ABC，PA平分∠BAC，PC平分∠ACB， ∵∠ABC+∠ACB+∠BAC=180°，∴∠PBC+∠PCA+∠PAB=90°. 6.已知等边三角形的内切圆半径， 外接圆半径分别为r，R，则r:R=______.分析:等边三角形的内切圆和外接圆是同心圆，内切圆半径是圆心到边的距离，外接圆的半径是圆心到顶点的距离，所以r: R=1:2.
 
 
 
切线长定理
圆的切线长的概念
圆的切线长定理
三角形的内切圆及内心的概念
课程结束
版权声明
人教统编版高中语文选择性必修上册
教习网//m.enxinlong.com/（以下简称“本网站”）系属深圳市智学帮科技有限公司（以下简称“本公司”）旗下网站，为维护本公司合法权益，现依据相关法律法规作出如下郑重声明：1.本文件仅用于个人学习、研究，不得用于商业性或盈利性用途，不得侵犯本司及相关权利人的合法权利。一旦发现侵权，本公司将联合司法机关获取相关用户信息并要求侵权者承担相关法律责任。2.本网站上所有原创内容，是本公司依据相关法律法规，安排专项经费运营规划，组织老师创作完成，著作权归属本公司所有。3.经由网站用户上传至本网站的课件、教案、学案、试卷等内容，其作品仅代表作者本人观点，本网站不保证其内容的有效性，凡因本作品引发的任何法律纠纷，均由上传用户承担法律责任，本网站仅有义务协助司法机关了解事实情况。
兼职招募
人教统编版高中语文选择性必修上册
教习网（m.enxinlong.com）专为 K12教育老师提供同步备课资料下载、教学经验学习等服务的互联网教育平台。为了进一步完善网站的资料体系，最大化满足用户的精品资源需求，现诚邀全国各地优秀一线老师加入教习网兼职创作老师团队，参与资源建设，获取高额现金收益。兼职招募详情请看：//m.enxinlong.com/article-5396.html
公益助学
人教统编版高中语文选择性必修上册
教习网诚挚地为各位老师推荐两款免费的朗读小程序，可用于课前预习、课中学习和课后复习，打开微信扫下方二维码即可使用，欢迎分享广大师生使用。
福利社群
人教统编版高中语文选择性必修上册
查看下方网页链接，扫码添加客服加入教习网专属福利社群： 更多福利，等您来领取：//m.enxinlong.com/act/event/pc/fuli.html