



初中数学人教版九年级上册24.2.2 直线和圆的位置关系完美版课件ppt
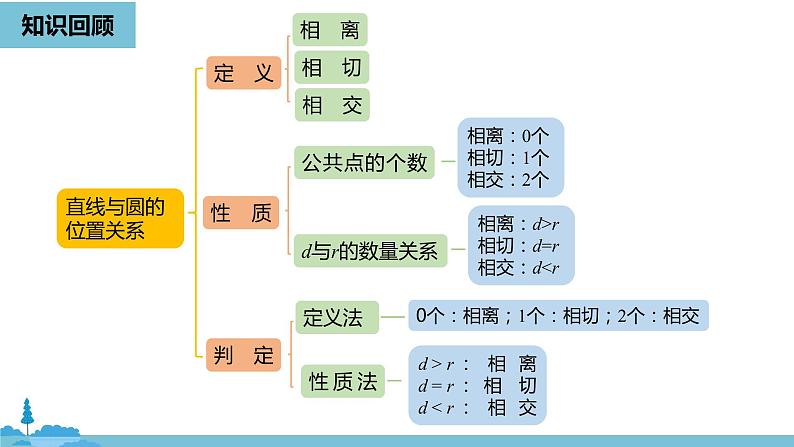
展开相离:d>r相切:d=r相交:d
d>r:相离d=r:相切d
1.会判定一条直线是否是圆的切线并会过圆上一点作圆的切线.
2.理解并掌握圆的切线的判定定理及性质定理.
3.能运用圆的切线的判定定理和性质定理解决问题.
转动雨伞时飞出的雨滴,用砂轮磨刀时擦出的火花,都是沿着什么方向飞出的?
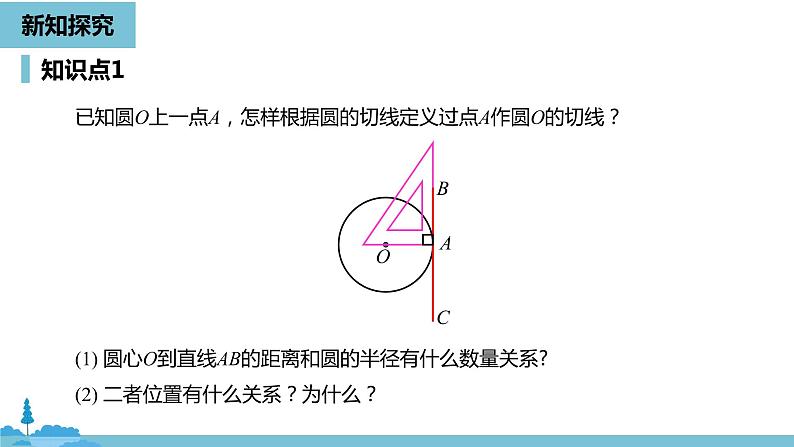
已知圆O上一点A,怎样根据圆的切线定义过点A作圆O的切线?
(1) 圆心O到直线AB的距离和圆的半径有什么数量关系?(2) 二者位置有什么关系?为什么?
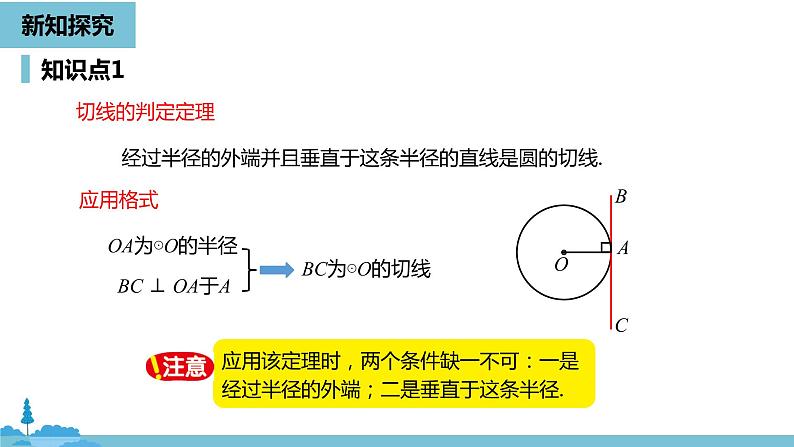
经过半径的外端并且垂直于这条半径的直线是圆的切线.
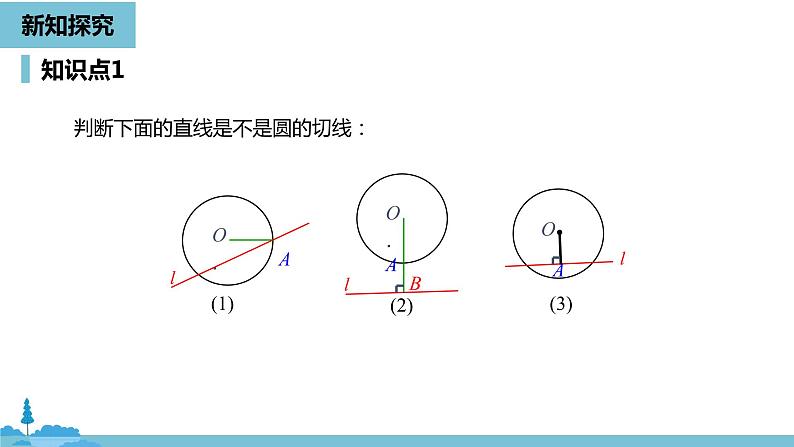
判断下面的直线是不是圆的切线:
判断一条直线是一个圆的切线有三个方法:
1.定义法:与圆有唯一公共点的直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径,即d=r;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
(1) 有交点,连半径,证垂直;(2) 无交点,作垂直,证半径.
证切线时辅助线的添加方法:
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D = 30°.求证:CD是⊙O的切线.
解:如图,连接OC.因为AC=CD,∠D=30°,所以∠A= ∠D = 30°.因为OA=OC,所以∠ACO=∠A = 30°,所以∠COD=60°,所以∠OCD=90°,即OC⊥CD.所以CD是⊙O的切线.
如图,如果直线l是⊙O 的切线,点A为切点,那么OA与l垂直吗?
∵直线 l 是⊙O 的切线,A是切点,
圆的切线垂直于过切点的半径.
(1) 假设AB与CD不垂直,过点O作一条直线垂直于CD,垂足为M.
(2) 则OM
作出小⊙O的同心圆大⊙O,CD切小⊙O于点A,且A点为CD的中点,连接OA,根据垂径定理,则CD ⊥OA,即圆的切线垂直于经过切点的半径.
(1) 经过圆心且垂直于切线的直线必过切点;(2) 经过切点且垂直于切线的直线必过圆心.
(2018∙常州中考)如图,AB是⊙O的直径,MN是⊙O的切线,切点为N,如果∠MNB =52°,那么∠NOA的度数为( )
A.76°B.56°C.54°D.52°
解:∵MN是⊙O的切线,∴ON⊥NM,∴∠ONM=90°,∴∠ONB=90°-∠MNB=90°-52°=38°,∵ON=OB,∴∠B=∠ONB=38°,∴∠NOA=2∠B=76°.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=40°,则∠ABD的度数是( )
A.30°B.25°C.20°D.15°
解:∵AC是⊙O的切线,∴∠OAC=90°,∵∠C=40°,∴∠AOC=50°,∵OB=OD,∴∠ABD=∠BDO,∵∠ABD+∠BDO=∠AOC,∴∠ABD=25°.
如图,AB是⊙O的直径,直线 l1 , l2 是⊙O的切线,A, B是切点, l1 , l2 有怎样的位置关系?证明你的结论.
解:l1∥l2,证明:∵直线 l1,l2是⊙O的切线,∴l1⊥AB,l2⊥AB,∴l1∥l2.
如图,在Rt△ABC中,∠ABC=90° ,∠BAC的平分线交BC于点D.以D为圆心,DB为半径作⊙D.求证:AC与⊙D相切.
解:过点D作DE⊥AC于点E,如图所示.因为∠ABC=90°,所以AB⊥BC,又AD平分∠BAC,DE⊥AC,所以DE=DB,所以AC与⊙D相切.
经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
圆的切线垂直于经过切点的半径
有切线时常用辅助线添加方法: 见切线,连切点,得垂直
(日照中考)如图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长交⊙O于点C,连接AC, AB=10,∠P=30° ,则AC的长度是( )
九年级上册24.2.2 直线和圆的位置关系图片课件ppt: 这是一份九年级上册24.2.2 直线和圆的位置关系图片课件ppt,共18页。PPT课件主要包含了CONTENTS,切线长,切线长定理,巩固应用等内容,欢迎下载使用。
数学九年级上册24.2.2 直线和圆的位置关系课文ppt课件: 这是一份数学九年级上册24.2.2 直线和圆的位置关系课文ppt课件,共17页。PPT课件主要包含了d与r的数量关系,点在圆内,点在圆上,点在圆外,点与圆的位置关系,交点数,直线与圆的位置关系,动画演示,同心圆,没有公共点等内容,欢迎下载使用。
人教版九年级上册24.2.2 直线和圆的位置关系课文内容ppt课件: 这是一份人教版九年级上册24.2.2 直线和圆的位置关系课文内容ppt课件,共12页。PPT课件主要包含了知识回顾,新知学习,切线的判定定理,对定理的理解,联系生活,证明连接OC,∴OC⊥AB,例题赏析,∴TA⊥OA,∴l1⊥OA等内容,欢迎下载使用。













