初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理完美版ppt课件

这是一份初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理完美版ppt课件，共23页。PPT课件主要包含了SA+SBSC，SAa2，SBb2，SCc2，a2+b2c2，由此我们猜想出，证明思路1，证明思路2，美丽的勾股树，感悟与反思等内容，欢迎下载使用。

毕达哥拉斯古希腊著名哲学家、数学家、天文学家
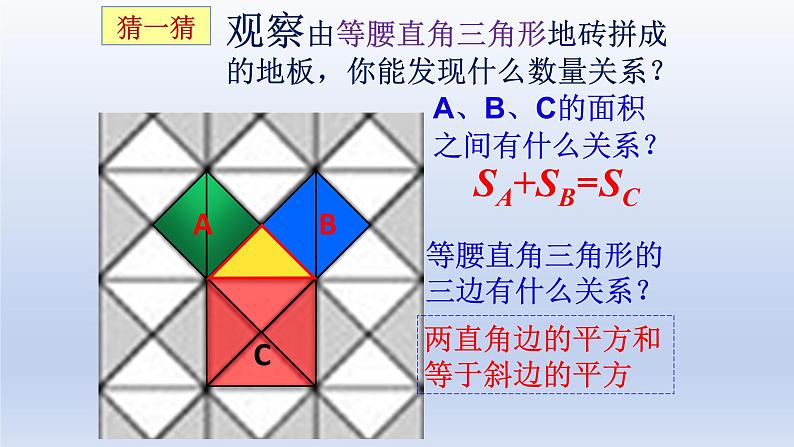
观察由等腰直角三角形地砖拼成的地板，你能发现什么数量关系？
A、B、C的面积之间有什么关系？
两直角边的平方和等于斜边的平方
等腰直角三角形的三边有什么关系？
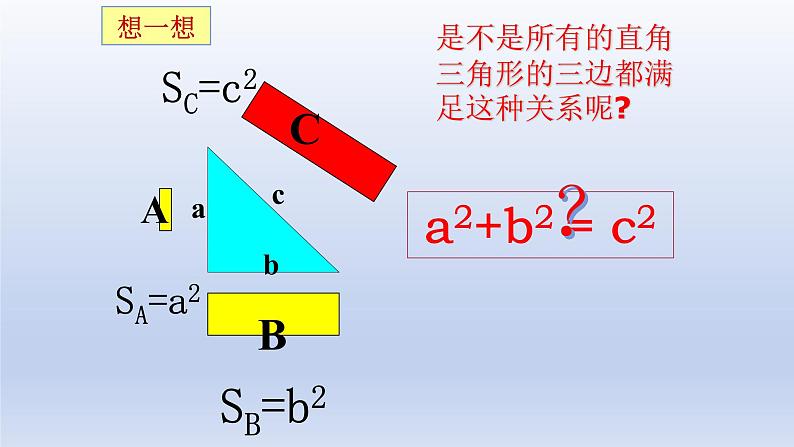
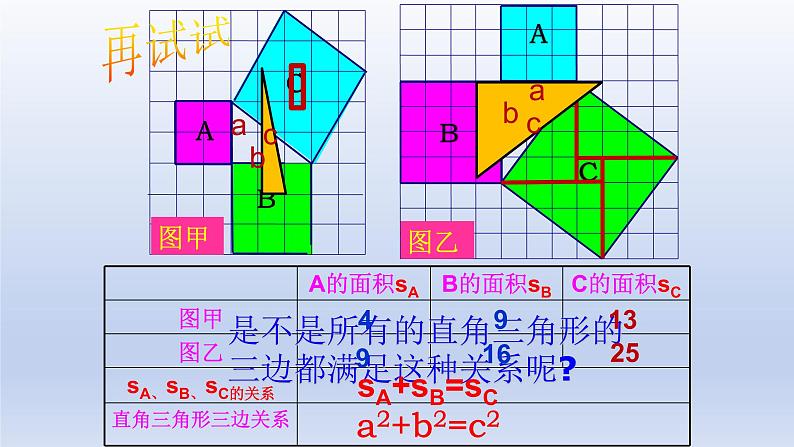
是不是所有的直角三角形的三边都满足这种关系呢?
如果直角三角形两直角边长分别为a,b, 斜边长为c,那么 a2 + b2 = c2.
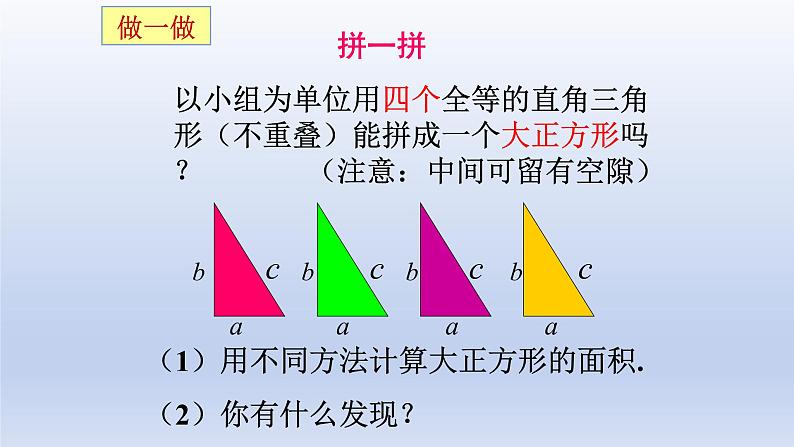
拼一拼以小组为单位用四个全等的直角三角形（不重叠）能拼成一个大正方形吗？ （注意：中间可留有空隙）
（1）用不同方法计算大正方形的面积.（2）你有什么发现？
还可看作: 四个直角三角形 + 一个小正方形
经过证明被确认正确的命题叫做定理.
如果直角三角形两直角边分别为a，b，斜边为c，那么
a2 + b2 = c2
即：直角三角形两直角边的平方和 等于斜边的平方.
为什么叫勾股定理这个名称呢？
较 短 直 角 边
25OO年前，在西方，因为是毕达哥拉斯最先发现这个定理的，所以西方人通常称勾股定理为“毕达哥拉斯定理” ．
我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就曾提出， “勾三、股四、弦五”，所以勾股定理又叫“商高定理”
例1.如图，在Rt△ABC中,∠ABC=90°, AB=8，BC=6，求图中直角三角形的 边AC的长度。
解：在Rt△ABC中，∠ABC=90°， 根据勾股定理得，
∵AC > 0 ∴AC =
求下列直角三角形中未知边的长:
2.已知直角三角形的三边长分别为 a、b、c.若 a = 6 ,b = 8,求 c .
　 练习1　如图，所有的三角形都是直角三角形，四边形都是正方形，已知正方形A,B,C,D 的边长分别是12，16，9，12 .求最大正方形E 的面积．
必做题：1.《教材》P28 1 7 2.自学课本P25-26选做题：（1）课本第71页“阅读与思考”，了解勾股 定理的多种证法.（2）有兴趣的学生上网查阅了解勾股定理的 有关知识并写一篇小论文.
说不定你也可以创造一种新的证明方法呢！