






初中数学人教版八年级下册17.1 勾股定理一等奖课件ppt
展开1、了解勾股定理的文化背景,体验勾股定理的探索过程, 掌握勾股定理反映的数量关系;2、会用拼图法、面积法证明勾股定理;3、能用勾股定理解决一些简单问题。
除地球外,别的星球上有没有生命呢?
我国著名数学家华罗庚在多年前曾提出这样的设想:向太空发射一种图形,因为这种图形在几千年前就已经被人类所认识,如果他们是“文明人”,也必定认识这种图形。
自古以来,人类就不断发出这样的疑问,特别是近年来不断出现的UFO事件,更让人们相信有外星人的说法,如果真的有,那我们怎么和他们交流呢?
那么这到底是一种什么样的图形呢?它真的有那么大的魅力吗?
下面就让我们通过时光隧道,和古希腊的数学家毕达哥拉斯一起来研究这种图形吧。
相传毕达哥拉斯有一次他在朋友家做客时,发现朋友家用砖铺成的地面中反映了A、B、C三者面积之间的数量关系,进而发现直角三角形三边的某种数量关系。
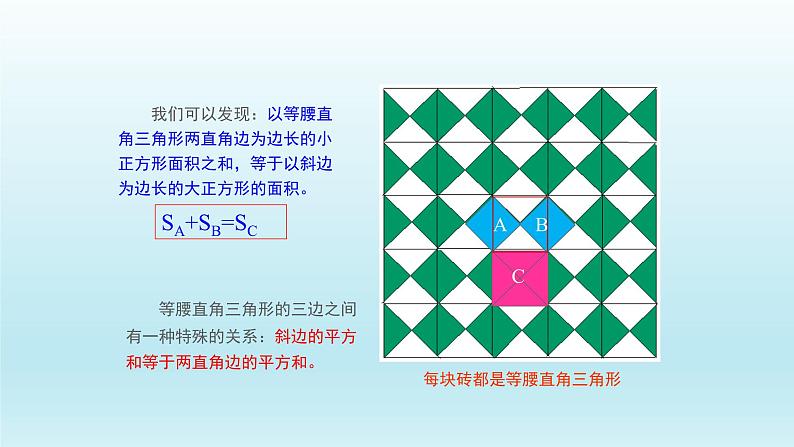
我们也来观察右图的地面,你能发现A、B、C面积之间有什么数量关系吗?
每块砖都是等腰直角三角形哦
等腰直角三角形的三边之间有一种特殊的关系:斜边的平方和等于两直角边的平方和。
每块砖都是等腰直角三角形
我们可以发现:以等腰直角三角形两直角边为边长的小正方形面积之和,等于以斜边为边长的大正方形的面积。
探究:SA+SB=SC 在下图中还成立吗?
A的面积是 个单位面积。
B的面积是 个单位面积。
C的面积是 个单位面积。
你是怎样得到正方形C的面积的?与同伴交流交流。
(图中每个小方格是1个单位面积)
问题2:式子SA+SB=SC能用直角三角形的三边a、b、c来表示吗?
问题4:那么直角三角形三边a、b、c之间的关系式是:
至此,我们在网格中验证了:直角三角形两条直角边上的正方形面积之和等于斜边上的正方形面积,即SA+SB=SC。
问题1:去掉网格结论会改变吗?
问题3:去掉正方形结论会改变吗?
命题1:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
是不是所有的直角三角形都具有这样的结论呢?光靠实验和猜想还不能把问题彻底搞清楚。
这就需要我们对一般的直角三角形进行证明。下面我们就一起来探究,看一看我国古代数学家赵爽是怎样证明这个命题的。
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子。你能做到吗?试试看。
现在,我们已经证明了命题1的正确性,在数学上,经过证明被确认为正确的命题叫做定理,所以命题1在我国叫做勾股定理。
即:直角三角形两直角边的平方和等于斜边的平方。
勾股定理:如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
我国是最早了解勾股定理的国家之一。三千多年前,周朝数学家商高就提出了“勾三股四弦五”的说法。
为什么叫勾股定理这个名称呢?
国外又叫毕达哥拉斯定理
原来在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。于是我国古代学者就把直角三角形中较短直角边称为“勾”,较长直角边称为“股”,斜边称为“弦”。由于命题1反映的正好是直角三角形三边的关系,所以叫做勾股定理。
如图,大风将一根木制旗杆吹裂,随时都可能倒下,十分危急。接警后“119”迅速赶到现场,并决定从断裂处将旗杆折断。现在需要划出一个安全警戒区域,那么你能确定这个安全区域的半径至少是多少米吗?
1.图中已知数据表示面积,求表示边的未知数x、y的值。
2.已知S1=1,S2=3,S3=2,S4=4,求S5、S6、S7的值。
1、本节课我们学到了什么?
通过学习,我们知道了著名的勾股定理,掌握了从特殊到一般的探索方法,还学会到了拼图证明的方法。
2、学了本节课后我们有什么感想?
我们发现有些数学结论就存在于平常的生活中,需要我们用数学的眼光去观察、思考、发现。
勾股定理:直角三角形两直角边长的平方和等于斜边长的平方。
如果在Rt△ABC中,∠C=90°,那么
1、能利用勾股定理解决实际问题。2、理解立体图形中两点距离最短问题。
1、求出下列直角三角形中未知的边。
①在解决上述问题时,每个直角三角形需要知道几个条件呢?②直角三角形哪条边最长?
2、在长方形ABCD中,宽AB为1m,长BC为2m,求AC长。
在Rt△ABC中,∠B=90°,由勾股定理可知:
一个门框尺寸如图所示。
①若有一块长3米,宽0.8米的薄木板,怎样才能让木板从门框通过呢?②若薄木板长3米,宽1.5米呢?③若薄木板长3米,宽2.2米呢?为什么?
∵木板的宽2.2米大于1米,∴ 横着不能从门框通过;∵木板的长3米大于2米,∴竖着也不能从门框通过。
∴ 只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,要怎样求呢?
例1:有一个边长为50dm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
解:∵在Rt△ABC中,∠B=90°, AB=BC=50dm,
如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上的一点,测得CB=60m,AC=20m,你能求出A,B两点间的距离吗?(结果保留整数)
例2:一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m,如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗?
解:在Rt△ABC中,∵∠ACB=90°, ∴AC2+BC2=AB2,即 2.42+BC2=2.52,∴BC=0.7m。
由题意得:DE=AB=2.5m,DC=AC-AD=2.4-0.4=2(m)。
在Rt△DCE中,∵∠DCE=90°,∴DC2+CE2=DE2 ,即22+CE2=2.52,∴CE=1.5m,∴BE=1.5-0.7=0.8m≠0.4m。
答:梯子底端B不是外移0.4m。
练习:如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米。
①求梯子的底端B距墙角O多少米? ②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们算一算,梯子底端滑动的距离的近似值是多少呢?(结果保留两位小数)
例3:在我国古代数学著作《九章算术》中记载了一道有趣的问题。这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少尺?
解:设水池的深度AC为x尺,则芦苇高AD为(x+1)尺。
根据题意得:BC2+AC2=AB2
∴52+x2=(x+1)2
25+x2=x2+2x+1
∴x+1=12+1=13(尺)
答:水池的深度为12尺,芦苇的长度为13尺。
例4:如图,在棱长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是___。
分析:由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图)。
(1)如图,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,容易得出S1,S2,S3之间的关系为 。
(2)变式:你还能求出S1,S2,S3之间的关系式吗?
1、在Rt△ABC中,∠C=90°,已知:a=5,b=12,求c。(1)已知:b=6,c=10,求a。(2)已知:a=7,c=25,求b。
2、一直角三角形的一直角边长为7,另两条边长为两个连续整数,求这个直角三角形的周长。
3、如图,受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4、一架长为5m的梯子,斜立靠在一竖直的墙上,这时梯子下端距离墙的底端的距离为3m,若梯子顶端下滑了1m,则梯子底端将外移_____。5、如图,要在高为3m,斜坡为5m的楼梯表面铺地毯,地毯的长度至少需要_____m。6、把直角三角形两条直角边同时扩大到原来的3倍,则其斜边________________。
7、在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处,另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高________米。
本节课我们主要学习了勾股定理的实际应用,关键是将实际问题转化为数学问题,再用勾股定理等知识来解答。
我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等。学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,AB=A'B',AC=A'C',求证:△ABC≌△A'B'C'。
证明:在Rt△ABC和Rt△A'B'C'中,∠C=90°,根据勾股定理,得:又∵AB=A'B',AC=A'C',∴BC=B'C',∴△ABC≌△A'B'C'。
2、若一个直角三角形两条直角边长是3和2,那么第三条边长是多少?
1、已知直角三角形的两边长分别为5和12,求第三边。
1、能利用勾股定理,根据已知直角三角形的两边长求第三条边长;并在数轴上表示无理数。2、体会数与形的密切联系,增强应用意识,提高运用勾股定理解决问题的能力。3、培养数形结合的数学思想。
数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
1、请你在作业纸上画图,在数轴上画出表示 的点。
2、你能在数轴上画出表示 的点吗?试一试!
利用勾股定理作出长为 ……的线段。
例:已知在Rt△ABC中,∠C=90°,CD⊥BA于D,∠A=60°,CD= ,求线段AB的长。
1、如图是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最少走多少厘米呢?
2、已知:如图,等边△ABC的边长是6cm。(1)求等边△ABC的高。 (2)求△ABC的面积。
初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理完美版ppt课件: 这是一份初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理完美版ppt课件,共23页。PPT课件主要包含了SA+SBSC,SAa2,SBb2,SCc2,a2+b2c2,由此我们猜想出,证明思路1,证明思路2,美丽的勾股树,感悟与反思等内容,欢迎下载使用。
初中数学人教版八年级下册17.1 勾股定理教学演示课件ppt: 这是一份初中数学人教版八年级下册17.1 勾股定理教学演示课件ppt,共19页。PPT课件主要包含了学习目标,复习引入,实际问题,数学问题,合作探究,知识要点,证明“HL”,类比迁移,课堂小结等内容,欢迎下载使用。
初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理图文ppt课件: 这是一份初中数学人教版八年级下册第十七章 勾股定理17.1 勾股定理图文ppt课件,共15页。PPT课件主要包含了赵爽弦图的证法,化简得,a2+b2c2,证法一,证法二等内容,欢迎下载使用。













