初中数学人教版八年级下册17.1 勾股定理教学演示课件ppt

这是一份初中数学人教版八年级下册17.1 勾股定理教学演示课件ppt，共19页。PPT课件主要包含了学习目标，复习引入，实际问题，数学问题，合作探究，知识要点，证明“HL”，类比迁移，课堂小结等内容，欢迎下载使用。

1.会运用勾股定理的数学模型解决现实世界的实际问题.
3.经历把实际问题转化成数学问题，利用勾股定理解决的过程.
2.能用勾股定理证明直角三角形全等的“斜边、直 角边”判定定理.
1.叙述勾股定理的内容
2. 矩形的一边长是5，对角线是13，则它的面积是 .
3.在△ABC中，AB=15，AC=13，高AD=12，则△ABC的周长为（ ）（A）42 （B）32（C）42或32 （D）30或35
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2
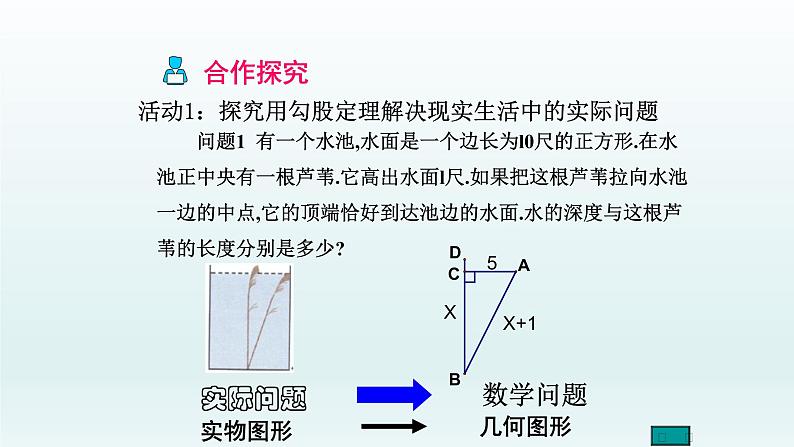
问题1 有一个水池,水面是一个边长为l0尺的正方形.在水池正中央有一根芦苇.它高出水面l尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?
活动1：探究用勾股定理解决现实生活中的实际问题
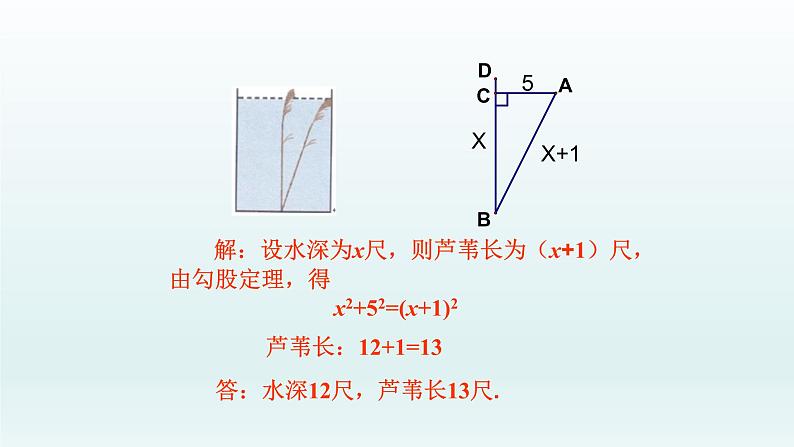
解：设水深为x尺，则芦苇长为（x+1）尺，由勾股定理，得
x2+52=(x+1)2
芦苇长：12+1=13
答：水深12尺，芦苇长13尺.
利用勾股定理解决实际问题的一般步骤：
（1）读懂题意，分析已知、未知间的关系；
（2）构造直角三角形；
（3）利用勾股定理等列方程或方程组；
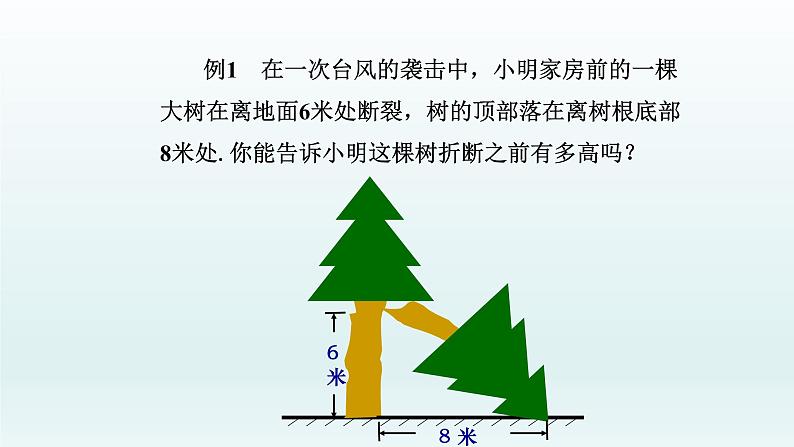
例1 在一次台风的袭击中，小明家房前的一棵大树在离地面6米处断裂，树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗？
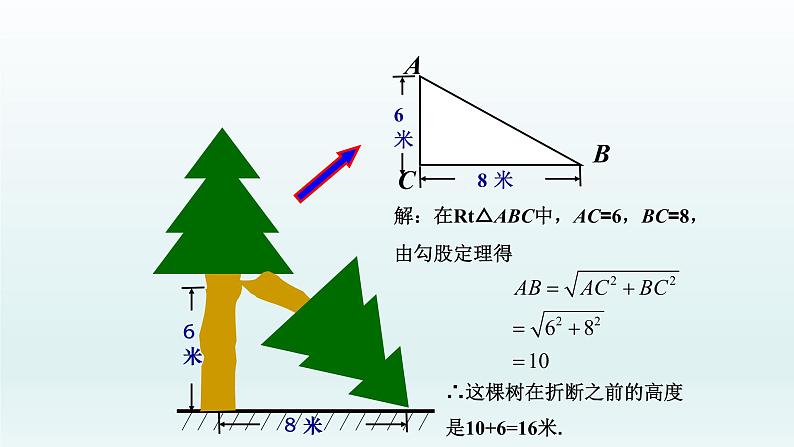
解：在Rt△ABC中，AC=6，BC=8，由勾股定理得
∴这棵树在折断之前的高度是10+6=16米.
　　问题1　在八年级上册中，我们曾经通过画图得到结论：斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后，你能证明这一结论吗？
　　证明：在Rt△ABC 和Rt△A B C 中，∠C=∠C′=90°，根据勾股定理，得
∴△ABC≌△A B C （SSS）
　　证明： ∵ AB=A B ， AC=A C ， ∴　BC=B C ．
　 问题2　我们知道数轴上的点有的表示有理数，有的表示无理数，你能在数轴上画出表示 的点吗？
探究思路：把握题意——找关键字词——连接相关知识——建立数学模型（建模）
直角边长为整数2，3的直角三角形的斜边为 .
活动2：探究用勾股定理在数轴上表示无理数
用同样的方法，你能否在数轴上画出表示 ， ，…
用同样的方法，你能否在数轴上画出表示 ， …
利用勾股定理表示无理数的方法
（1）利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.如本题中的 看成直角边分别为2和3的直角三角形的斜边； 看成是直角边分别为1和2的直角三角形的斜边等.
（2）以原点O为圆心，以无理数斜边长为半径画弧与数轴存在交点，在原点左边的点表示是负无理数，在原点右边的点表示是正无理数.
例2 如图,以数轴上的单位线段长为边作一个正方形,以原点为圆心,以正方形的对角线长为半径,画弧交数轴于点A,则A点表示的数是（ ）
1.运用勾股定理解决实际问题的方法是什么？
（2）注意：运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.
2.用勾股定理作出长度为无理数的线段的思路是什么？
构造直角三角形，即把无理数线段看成是两直角边都为整数的斜边.