初中数学人教版八年级上册13.3.1 等腰三角形优质课件ppt

这是一份初中数学人教版八年级上册13.3.1 等腰三角形优质课件ppt，共11页。PPT课件主要包含了等腰△ABC中，简称等边对等角，等腰三角形性质一，等腰三角形性质二，CAD，ADC，同步练习，小试牛刀，大显身手，拓展提高等内容，欢迎下载使用。

在大家的印象里，什么样的三角形叫做等腰三角形？
有两条边相等的三角形叫做等腰三角形
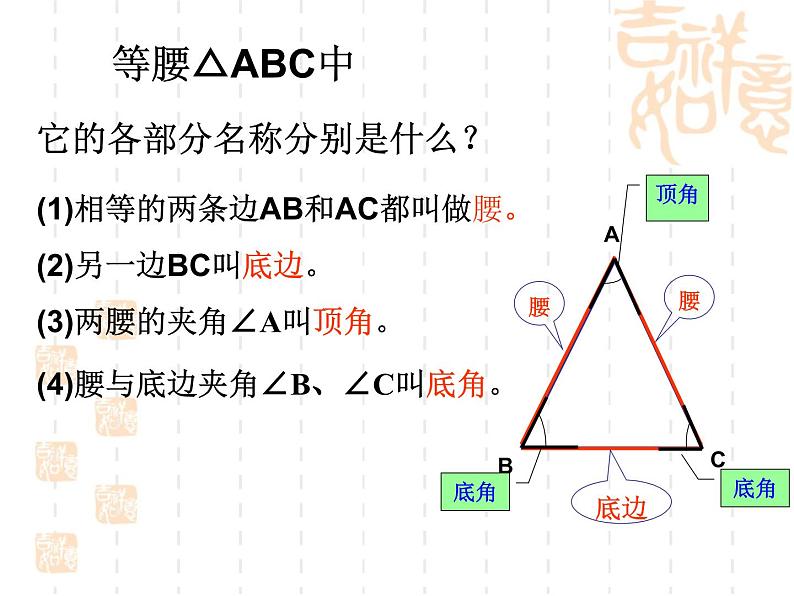
它的各部分名称分别是什么？
(1)相等的两条边AB和AC都叫做腰。
(2)另一边BC叫底边。
(3)两腰的夹角∠A叫顶角。
(4)腰与底边夹角∠B、∠C叫底角。
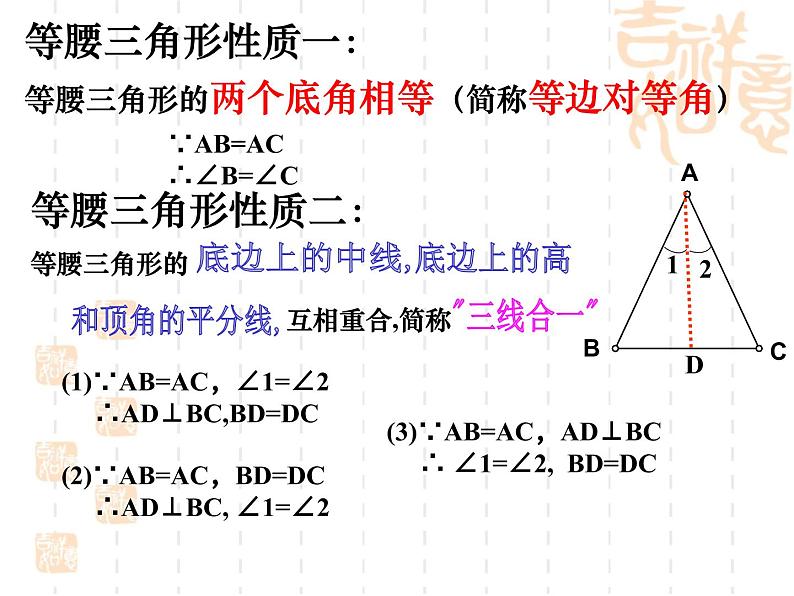
等腰三角形的两个底角相等
∵AB=AC∴∠B=∠C
(1)∵AB=AC，∠1=∠2 ∴AD⊥BC,BD=DC
(2)∵AB=AC，BD=DC ∴AD⊥BC, ∠1=∠2
(3)∵AB=AC，AD⊥BC ∴ ∠1=∠2, BD=DC
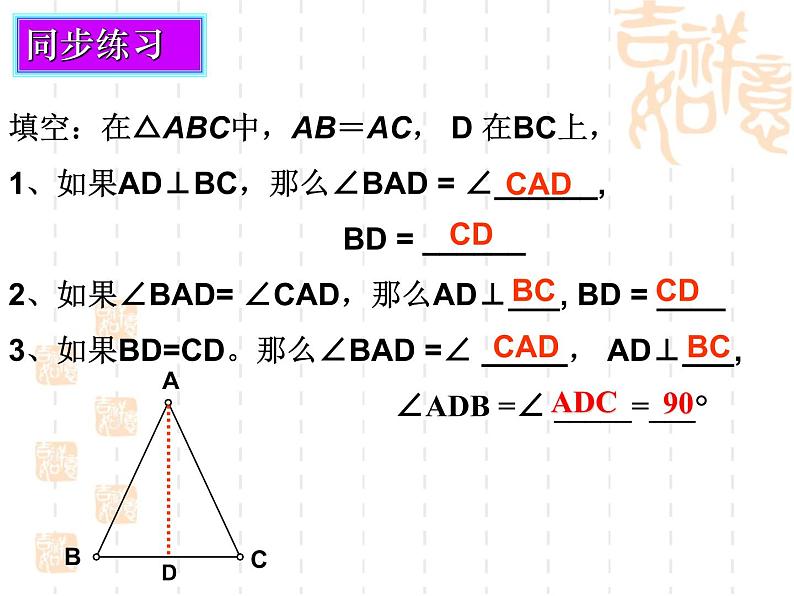
填空：在△ABC中，AB＝AC， D 在BC上，1、如果AD⊥BC，那么∠BAD = ∠______, BD = ______2、如果∠BAD= ∠CAD，那么AD⊥___, BD = ____ 3、如果BD=CD。那么∠BAD =∠ _____， AD⊥___, ∠ADB =∠ _____=___°
如果一个三角形有两个角相等，那么这两个角所对的边也相等。（简写成“等角对等边”）
两条边相等的三角形叫等腰三角形。
∵AB=AC∴△ABC是等腰三角形
∵∠B=∠C∴AB=AC∴△ABC是等腰三角形
120°、30°、30°
1.如图，△ABC中，AB=AC，E为BC中点，BD⊥AC，垂足为D，∠EAD=20°。求：∠ABD
∵AB=AC∴∠ABC=∠C(等边对等角)又∵E为BC中点∴ AE为∠BAC的角平分线（等腰三角形的“三线合一”） ∴ ∠BAC=2∠1=40°(角平分线性质) 又∵ BD⊥AC ∴ ∠ABD=90°－40°=50°
1.如图，在△ABC中，∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F,AB=9,AC=8求：(1)图中有几个等腰三角形，(2)△AEF的周长。（说明理由）
图中有两个等腰三角形∵OB为∠ABC的平分线(已知)
∴∠1=∠2 (角平分线的性质)　
∴∠2=∠5(两直线平行,内错角相等)
∴∠1=∠5(等量代换)
∴BE=EO(等角对等边)
∴△EBO为等腰三角形
同理:△FOC也为等腰三角形
∴ C△AEF=AE+AF+EF
（2）∵OE=BE OF=FC (已证)
=AE+AF+EO+FO
=AE+AF+EB+FC
∵AB=9, AC=8(已知)
∴C△AEF=9+8=17
答：△AEF的周长为17