数学八年级上册15.1 分式综合与测试评优课课件ppt

这是一份数学八年级上册15.1 分式综合与测试评优课课件ppt，共20页。PPT课件主要包含了分式的基本性质，约分与通分，分式的运算，4分式加减法法则，典型例题解析，方法小结，课时训练等内容，欢迎下载使用。

1.如果整式A除以整式B,可以表示成 的形式.且除式B中含有字母,那么称式子 为分式(fractin).
其中,A叫做分式的分子,B叫做分式的分母。
2.整式和分式统称有理式.
①整式和分式的区别在于：除式B中是否含有字母.
②分式的隐含条件是：分式的分母不等于0.
③分式的值为0的条件是：分子为0且分母不等于0.
1.分式的基本性质：分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变,用式子表示是：
(1)最大公因式的构成:①分子分母系数的最大公约数；②分子分母中相同因式的最低次幂.
(2)最简公分母的构成:①各分母系数的最小公倍数；②各分母中所有不同因式的最高次幂.
(其中M是不等于零的整式)
1.分式的乘除法法则:(1)两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母;
(2)两个分式相除,把除式的分子分母颠倒位置后,再与被除式相乘.
(3) 分式乘方:把分子分母各自乘方.
①同分母分式加减法的法则:分母不变,分子相加减.
②异分母分式加减法的法则:先通分,把异分母分式化为同分母分式.
(5)分式运算的原则:①凡遇到分子或分母是多项式,先分解因式,再约分或通分;②结果化成最简分式.
当x 时，分式 有意义。
题组训练(中考题选练)
3.计算： = .
4.在分式① ,② ,③ ,④ 中 ，最简分式的个数是 ( ) A.1 B.2 C.3 D.4
2. 计算： = .
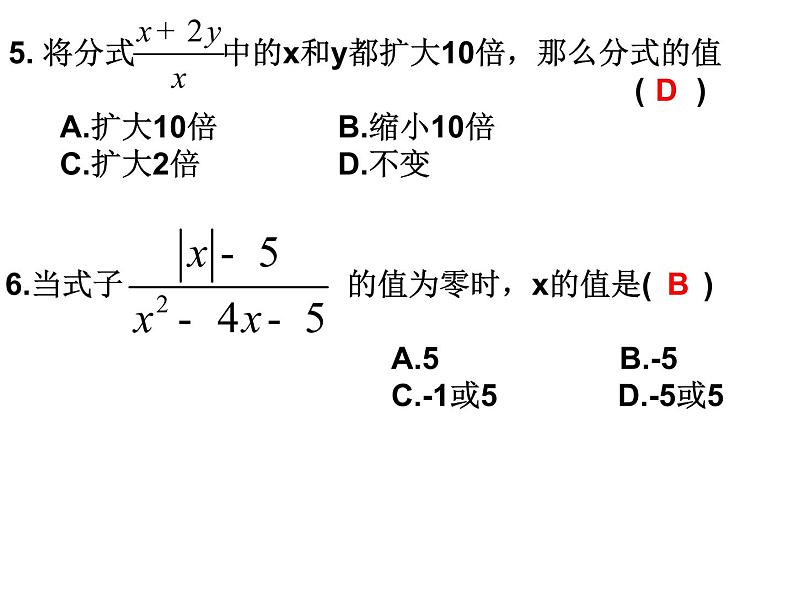
5. 将分式 中的x和y都扩大10倍，那么分式的值 ( ) A.扩大10倍 B.缩小10倍 C.扩大2倍 D.不变
【例1】 当a取何值时，分式 (1)值为零；(2)分式有意义?
【例3】 计算：(1) ；(2)［( )( )-3］÷( ).
解: 原式=［ ］÷( ) =［ ］ =( ) = = =
【例4】 化简求值：( ) ÷ ，其中a满足：a2+2a-1=0.
解：原式=［ ］× = × = × = =
又∵a2+2a-1=0，∴a2+2a=1, ∴原式=1
【例5】 化简： + + +
解：原式= = = =
1.当分式的值为零时，必须同时满足两个条件：①分子的值为零；②分母的值不为零.2.分式的混和运算应注意运算的顺序，同时要掌握通分、约分等法则，灵活运用分式的基本性质，注意因式分解、符号变换和运算的技巧，尤其在通分及变号这两个方面极易出错，要小心谨慎！
2.化简： 的结果： 。
3.化简：
4.当1＜x＜3时，化简 得 ( ) A.1 B.-1 C.3 D.-3
9:甲,乙两位采购员同去一家饲料公司采购两次饲料,两次饲料的价格有变化,两位采购员的购货方式也不同,其中甲每次购买1000千克,乙每次购买800元而不管购买多少饲料,设两次购买的饲料的单价分别为m元/千克和n元/千克(m,n为正数且不相等)那么甲,乙购买的平均单价谁更低?