初中数学人教版八年级上册14.2.1 平方差公式公开课课件ppt

这是一份初中数学人教版八年级上册14.2.1 平方差公式公开课课件ppt，共22页。PPT课件主要包含了a2−b2，这两数的平方差，平方差公式，合理加括号，这节课你有哪些收获等内容，欢迎下载使用。
计算下列多项式的积，你能发现什么规律？
(1) (x+1)(x-1）=
(2) (m+2)(m-2）=
(3) (2x+1)(2x-1）=
(a+b)(a−b),有
(a+b)(a−b)=
两数和与这两数差的积,
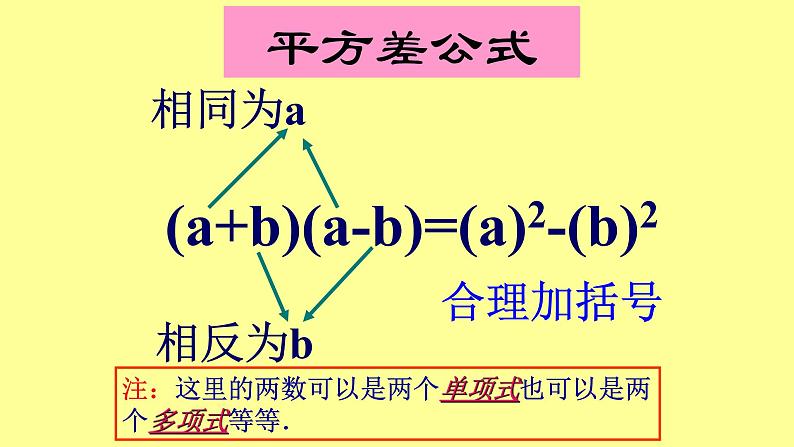
(a+b)(a-b)=(a)2-(b)2
注：这里的两数可以是两个单项式也可以是两个多项式等等．
1.先找出相同的项和相反的项，相同的项看作公式中的a，相反的项看作公式中的b ；
2. 再写成两项和乘以两项差的形式；
3.然后可以运用公式写出，即用相同项的平方减去相反项的平方。
判断下列式子是否可用平方差公式。
(1)(-a+b)(a+b) (2) (-a+b)(a-b) (3)(a+b)(a-c) (4)(2+a)(a-2) （5） (1-x)(-x-1)（6）(-4k3+3y2)(-4k3-3y2)
例1 运用平方差公式计算：
(1) (3x+2)(3x − 2）
(2) (b+2a)(2a − b）
(3) (− x+2y)(− x − 2y）
分析：在（1）中，可以把3x看成a,2看成b,即
(1) (3x+2)(3x − 2）=
( a+b) ( a − b) =
分析：在（2）中，可以把（ ）看成a,（　）看成b
(2) (b+2a)(2a − b）=
(2a+b)(2a − b）
分析：在（3）中，可以把（ ）看成a,（　）看成b
(3) (− x+2y)(− x − 2y）=
⑴ (a+1)(a-1)=
⑵ (3+x)(3-x)=
⑶ (a+2b)(a-2b)=
⑷ (3x+5y)(3x-5y)=
⑸ (10s-3t)(10s+3t)=
(3x)2-(5y)2
(10s)2-(3t)2
（6）(−3x+2)(−3x−2)
（8）(−3x+y)(3x+y)
（7）(−4a+3)(−4a−3)
（9）(y−x)(−x−y)
(10)(-m+n)(-m-n)=
例2：计算 （1）102×98 (2) (y+2)(y-2)-(y-1)(y+5)
（1）解：原式=(100+2)(100-2) =1002-22 =10000-4 =9996
(2)解：原式=y2-4-(y2+4y-5) =y2-4-y2-4y+5 =-4y+1
运用平方差公式计算：P108
(1) (a+3b)(a-3b）
(2) (3+2a)(-3+2a）
(3) (3x+4) (3x-4) – (2x+3) (3x-2)
(1) (a+3b)(a-3b）=
(2) (3+2a)(-3+2a）=
(2a+3)(2a-3）
(3) (3x+4)(3x-4)- (2x+3)(3x-2)
= 9x2- 42 -(6x2+5x-6)
= 9x2-16-6x2-5x+6
= 3x2-5x-10
（4）1992×2008
（1）1992×2008
=(2000 −8) ×(2000+8 )
=20002 −82
=4000 000−64
=3 999 936
（5）996×1004
（2）996×1004
=(1000 −4) ×(1000+4 )
=10002 −42
=1000 000−16
(1) (x+3)( )=x2-9
(2) (-1-2x)( 2x-1)=
(3) (m+n)( )=n2-m2
(4) ( )(-y-1)=1-y2
(5) (-3a2+2b2)( )=9a4-4b4
（1）(x+y)(x-y)(x2+y2)
解：原式 =(x2-y2)(x2＋y2)
（2） (x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)
解：原式= (x2－y2)(x2+y2)(x4+y4)(x8+y8)
=(x4－y4) (x4+y4)(x8+y8)
=(x8－y8 )(x8+y8)
（3） (3a＋b＋c)(3a＋b－c)解：原式=[(3a＋b) ＋c][(3a＋b) －c]=(3a＋b)2－c2=9a2＋6ab＋b2－c2