北师大版第五章 生活中的轴对称3 简单的轴对称图形优秀课件ppt

这是一份北师大版第五章 生活中的轴对称3 简单的轴对称图形优秀课件ppt，共28页。PPT课件主要包含了沿CA将纸折叠，3把纸展开，得到折痕CA和CB，操作讨论，AOBO，CACB，线段的垂直平分线，已知线段AB，两弧相交于点C和D，作线段的垂直平分线等内容，欢迎下载使用。

张店区政府为了方便居民的生活，计划在三个住宅小区A、B、C之间修建一个购物中心，试问，该购物中心应建于何处，才能使得它到三个小区的距离相等.
1. 理解线段垂直平分线的性质.
2. 能运用线段垂直平分线的性质解决实际问题．
3. 会用尺规作线段的垂直平分线，了解作图的道理．
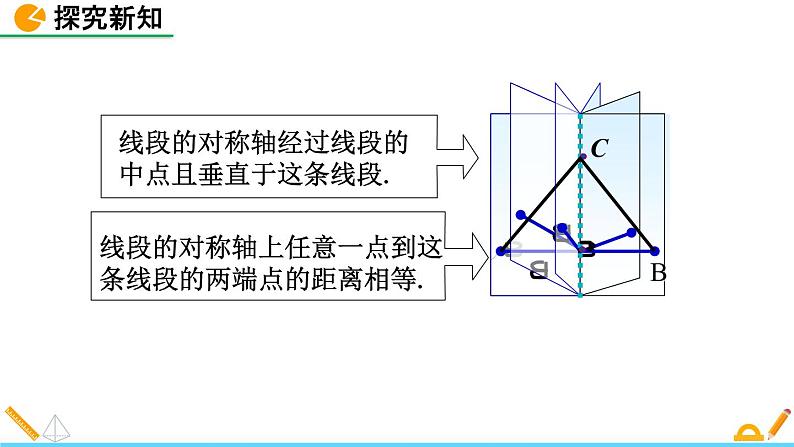
线段是轴对称图形吗？如果是，你能找出它的一条对称轴吗？这条对称轴与线段存在着什么关系？
线段的垂直平分线的性质定理
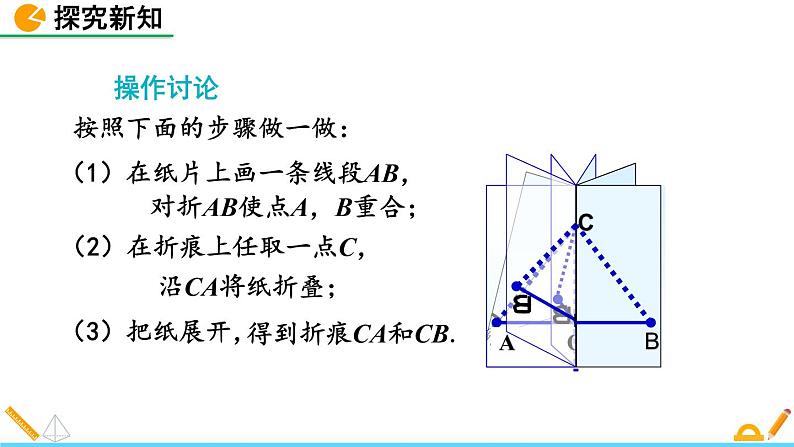
按照下面的步骤做一做：
（1）在纸片上画一条线段AB，
对折AB使点A，B重合；
折痕与AB的交点为O；
（2）在折痕上任取一点C，
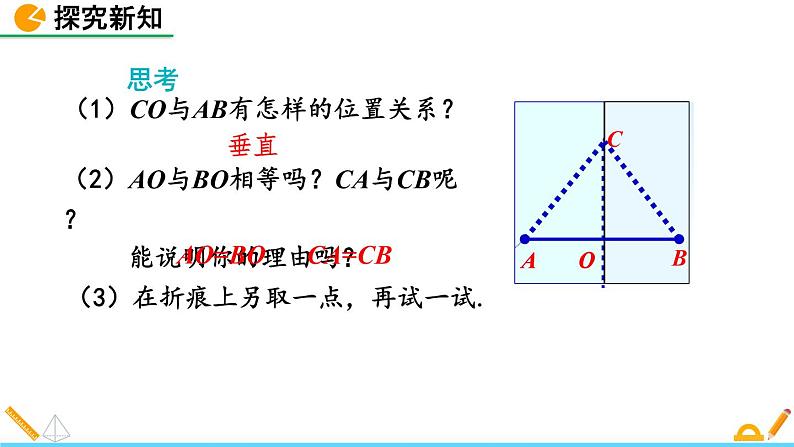
（1）CO与AB有怎样的位置关系？
（2）AO与BO相等吗？CA与CB呢？ 能说明你的理由吗？
（3）在折痕上另取一点，再试一试.
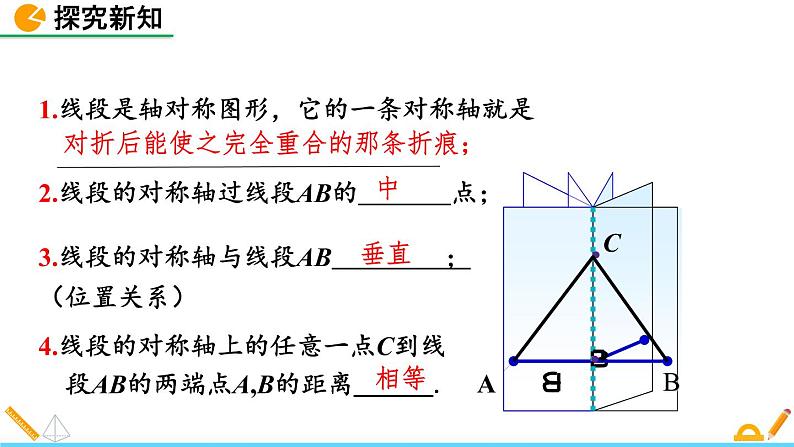
1.线段是轴对称图形，它的一条对称轴就是
对折后能使之完全重合的那条折痕；
2.线段的对称轴过线段AB的 点；
3.线段的对称轴与线段AB ；（位置关系）
4.线段的对称轴上的任意一点C到线 段AB的两端点A,B的距离______.
　　已知：如图，直线l⊥AB，垂足为C，AC =CB，点P 在l 上．　　试说明：PA =PB．
　　线段垂直平分线上的点到线段两端点的距离相等．
用数学语言表示为：因为 CA =CB，l⊥AB，所以 PA =PB．
　　解：因为　l⊥AB， 所以 ∠PCA =∠PCB．　　又 AC =CB，PC =PC，　　所以△PCA ≌△PCB（SAS）．　　所以PA =PB．
1.垂直于一条线段，并且平分这条线段的直线，叫作 这条线段的垂直平分线.
2.线段垂直平分线的性质： 线段垂直平分线上的点 到这条线段两个端点的 距离相等.
3.线段的对称轴是这条线段的垂直平分线.
例1 如图，DE是AC的垂直平分线，AB＝12厘米，BC＝10厘米，则△BCD的周长为(　　)
A．22厘米 B．16厘米C．26厘米 D．25厘米
解析：根据线段垂直平分线的性质得CD＝AD，故△BCD的周长为BD＋DC＋BC＝AD＋BD＋BC＝AB＋BC＝12＋10＝22(厘米)．
利用线段垂直平分线的性质求线段的长
如图，在△ABC 中，BC =8，AB 的中垂线交BC于D，AC 的中垂线交BC 与E，则△ADE 的周长等于___．
　　解：因为　AD⊥BC，BD =DC， 所以AD 是BC 的垂直平分线， 所以　AB =AC． 因为点C 在AE 的垂直平分线上， 所以　AC =CE．
例2　如图，AD⊥BC，BD =DC，点C 在AE 的垂直平分线上，AB，AC，CE 的长度有什么关系？AB+BD与DE 有什么关系？
　　所以　AB =AC =CE． 因为AB =CE，BD =DC， 所以AB +BD =CD +CE． 即　AB +BD =DE ．
已知:如图,ΔABC中,边AB，BC的垂直平分线交于P.试说明：PA=PB=PC . 　　　
利用尺规，作线段AB的垂直平分线.
作法：1.分别以点A和点B为圆心，以大于 AB一半的长为半径作弧，
求作：AB的垂直平分线.
2.作直线CD.直线CD就是线段AB的垂直平分线．
如图，如果点C不在直线l上，试和同学讨论，应采取怎样的步骤，过点C画出直线l的垂线？
作法：(1)以点C为圆心，以适当长为半径画弧，交直线l于点A、B；
(4)经过点C、D作直线CD．
1.（2020•呼伦贝尔）如图，AB=AC，AB的垂直平分线MN交AC于点D，若∠C＝65°，则∠DBC的度数是（　　）A．25°B．20°C．30°D．15°
2.（2020•枣庄）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC=6，AC=5，则△ACE的周长为（　　）A．8 B．11 C．16D．17
1.如图，直线CD是线段PB的垂直平分线，点P为直线CD上的一点，且PA=5，则线段PB的长为（ ） A. 6 B. 5 C. 4 D. 3
3.如图,AB是△ABC的一条边，DE是AB的垂直平分线，垂足为E，并交BC于点D，已知AB=8cm,BD=6cm,那么EA=_______, DA=_______.
4．如图，CD是AB的垂直平分线，若AC＝1.6 cm，BD＝2.3 cm，则四边形ACBD的周长为 _______cm.
解：因为DE是△ABC边AB的垂直平分线,所以EB=EA,所以△AEC的周长=AC+CE+EA=AC+CE+EB=AC+BC=4+5=9.
5.如图，DE是△ABC边AB的垂直平分线，交AB、 BC于D、E，若AC=4，BC=5，求△AEC的周长.
如图，已知AB比AC长2 cm，BC的垂直平分线交AB于点D，交BC于点E，△ACD的周长是14 cm，求AB和AC的长．
解：因为DE垂直平分BC，所以DB＝DC.因为AC＋AD＋DC＝14 cm，所以AC＋AD＋BD＝14 cm.即AC＋AB＝14 cm.又因为AB-AC＝2 cm，所以AB＝AC+2 cm.解得AC=6 cm ，AB=8cm所以AB长为8 cm，AC长为6 cm.
如图，某地由于居民增多，要在公路l边增加一个公共汽车站，A，B是路边两个新建小区，这个公共汽车站C建在什么位置，能使两个小区到车站的路程一样长(要求：尺规作图，保留作图痕迹，不写画法)?
解：连接AB，作AB的垂直平分线交直线l于O，交AB于E.因为EO是线段AB的垂直平分线，所以点O到A，B的距离相等，所以这个公共汽车站C应建在O点处，才能使到两个小区的路程一样长．
线段垂直平分线上的点到线段的两个端点的距离相等
见垂直平分线，得线段相等