初中数学北师大版七年级下册3 简单的轴对称图形优秀课件ppt

这是一份初中数学北师大版七年级下册3 简单的轴对称图形优秀课件ppt，文件包含课时3角平分线的性质pptx、课时3角平分线的性质doc等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

1.会用尺规作图法作一个角的平分线，知道作法的理论依据.（重点） 2.探究并证明角平分线的性质.（难点） 3.会用角平分线的性质解决实际问题.
如图是一个平分角的仪器，其中AB=AD，BC=DC.将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是这个角的平分线.你能说明它的道理吗？
理由如下：如图构成了△ADC和△ABC， ∵在△ADC和△ABC中， AD=AB， AC=AC， DC=BC， ∴△ADC≌△ABC（SSS），∴ ∠DAC=∠BAC. ∵点C在射线AE上， ∴AE是这个角的平分线.
知识点1 作已知角的平分线
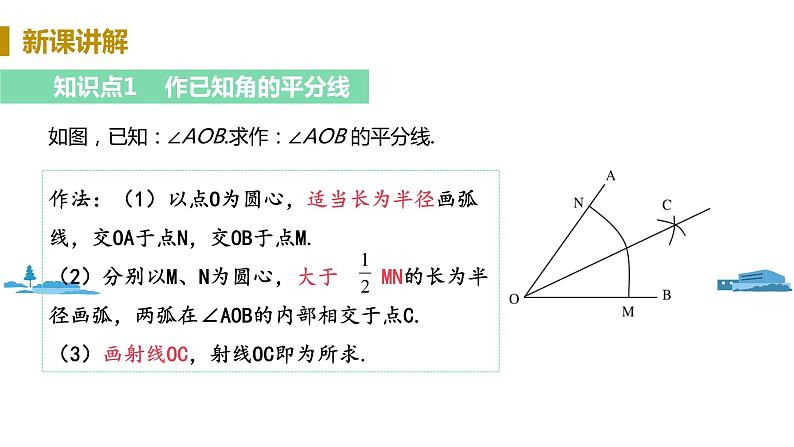
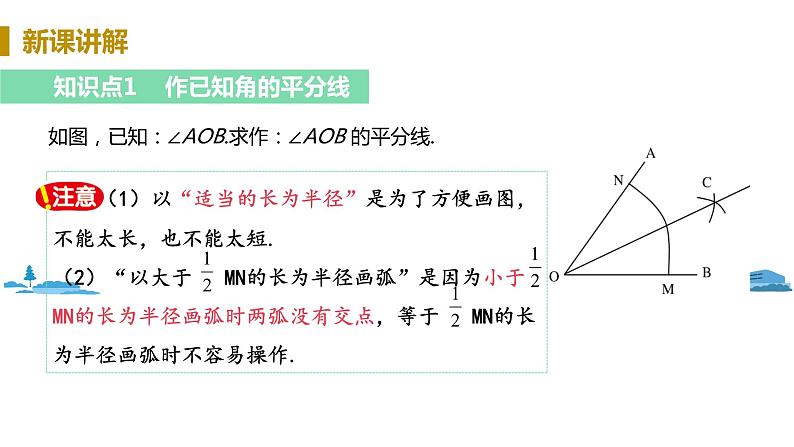
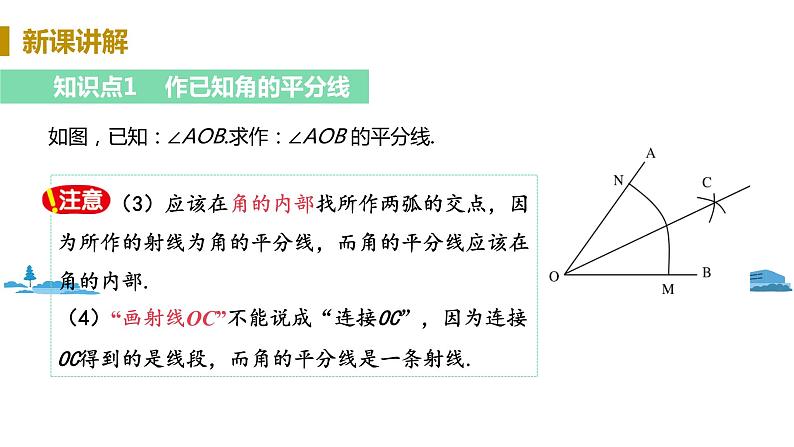
如图，已知：∠AOB.求作：∠AOB 的平分线.
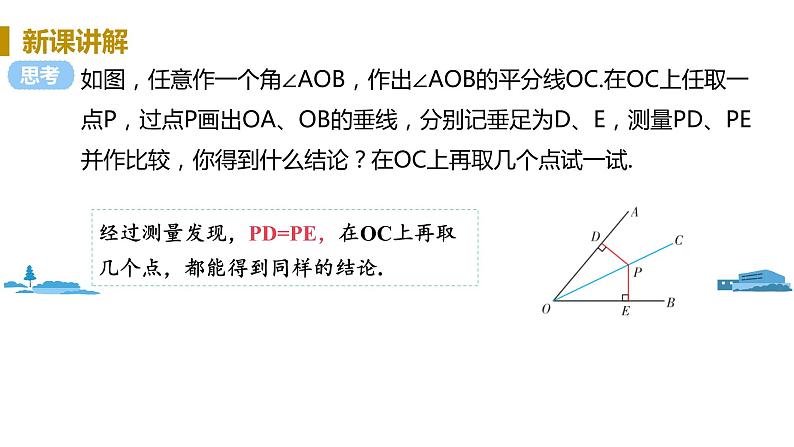
如图，任意作一个角∠AOB，作出∠AOB的平分线OC.在OC上任取一点P，过点P画出OA、OB的垂线，分别记垂足为D、E，测量PD、PE并作比较，你得到什么结论？在OC上再取几个点试一试.
经过测量发现，PD=PE，在OC上再取几个点，都能得到同样的结论.
知识点2 角平分线的性质
几何表示：如图，∵OC是∠AOB的平分线，点P是OC上一点，PD⊥OA，PE⊥OB，垂足分别为D，E.∴PD=PE.
如图，∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D、E.求证：PD=PE.
证明几何命题的一般步骤.（1）明确命题中的已知和求证；（2）根据题意，画出图形，并用符号表示已知和求证；（3）经过分析，找出由已知推出要证明的结论的途径，写出证明过程.
1 求证：三角形的一边的两端点到这条边上的中线所在的直线的距离相等.
已知，如图所示，AD为△ABC的中线，且CF⊥AD于点F，BE⊥AD交AD的延长线于点E.求证：BE=CF.
证明：∵AD为△ABC的中线， ∴BD=CD.∵CF⊥AD，BE⊥AD交AD的延长线于点E，∴∠BED=∠CFD=90°.在△BED和△CFD中， ∠BED=∠CFD， ∠BDE=∠CDF， BD=CD，∴△BED≌△CFD（AAS）， ∴BE=CF.
填空：下列结论一定成立的是（ ） ①如图1，OC平分∠AOB，点P在OC上，D，E分别为OA、OB上的点，则PD=PE. ②如图2，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E，则PD=PE. ③如图3，OC平分∠AOB，点P在OC上，PD┴OA，垂足分别为D.若PD=3，则点P到OB的距离为3.
①如图1，OC平分∠AOB，点P在OC上，D，E分别为OA，OB上的点，则PD=PE（PD、PE不是角平分线上的点到角两边的距离）. ②如图2，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D，E，则PD=PE（OC不是∠AOB的平分线）. ③如图3，OC平分∠AOB，点P在OC上，PD⊥OA，垂足分别为D.若PD=3，则点P到OB的距离为3（PD是∠AOB平分线OC上的点到OA的距离）.
如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB，DF⊥AC，垂足分别为E、F.求证：EB=FC.
证明：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC， ∴DE=DF. ∵在Rt△BDE和Rt△CDF中， BD=CD， DE=DF， ∴Rt△BDE≌Rt△CDF（HL）. ∴EB=FC.
角的平分线上的点到角的两边的距离相等
利用角平分线的性质解决实际问题
会用尺规作图法画出一个已知角的平分线
如图，OP为∠AOB 的平分线，PC⊥OA，PD⊥OB，垂足分别为C，D，则下列结论错误的是（ ）A.PC=PD B.∠CPO=∠DOP C.∠CPO=∠DPO D.OC=OD
如图，在△ABC中，∠C=90°，AC=BC，AD平分∠CAB，交BC于点D，DE⊥AB，垂足为E，若AB=8cm，则△DEB 的周长为（ ） A.10cm B.7cm C.8cm D.不能确定