




北师大版七年级下册2 频率的稳定性获奖ppt课件
展开某路口红绿灯的时间设置情况为:红灯40秒,绿灯60秒,黄灯4秒.试想一下,当人或车随意经过该路口时,遇到哪一种灯的可能性最大?遇到哪一种灯的可能性最小?根据什么?
1.通过试验让学生理解当试验次数较大时,试验频率稳定在某一常数附近,并据此能估计出某一事件发生的频率.
2. 大量重复试验得到频率的稳定值的分析.
3. 在活动中进一步发展学生合作交流的意识与能力,发展学生的辩证思维能力.
抛掷一枚图钉,落地后会出现两种情况:钉尖朝上 ,钉尖朝下.你认为钉尖朝上和钉尖朝下的可能性一样大吗?
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的.
我的直觉跟你一样,但我不知道对不对.
不妨让我们用试验来验证吧!
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
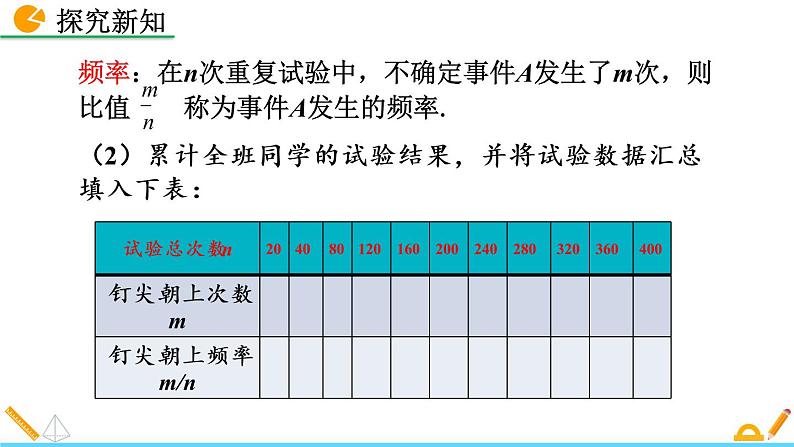
频率:在n次重复试验中,不确定事件A发生了m次,则比值 称为事件A发生的频率.
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
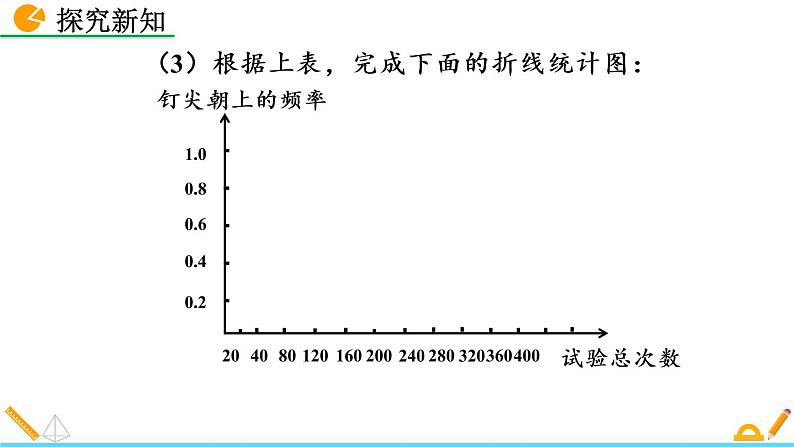
(3)根据上表,完成下面的折线统计图:
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察图像,钉尖朝上的频率的变化有什么规律?
在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)小军和小凡一起做了1000次掷图钉的试验,其中有640次钉尖朝上.据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大.你同意他们的说法吗?
不一样大,因为频率稳定在0.4左右.
不同意,因为实验数据太小.
例1 做重复试验:抛掷同一枚啤酒瓶盖1 000次.经过统计得“凸面向上”的频率约为0.44,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的频率稳定在( )
解析:瓶盖只有两面,“凸面向上”的频率约为0.44,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的频率稳定在1-0.44=0.56.故选D.
小明练习射击,共射击60次,其中有38次击中靶子,由此可估计,小明射击一次击中靶子的频率稳定在( ) A.38% B.60% C.约63% D.无法确定
例2 在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色,…如此大量摸球实验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,对此实验,他总结出下列结论:①若进行大量摸球实验,摸出白球的频率稳定于30%;②若从布袋中任意摸出一个球,该球是黑球的频率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是 .
解:因为在一个不透明的布袋中,红球、黑球、白球共有若干个,其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%,所以①若进行大量摸球实验,摸出白球的频率稳定于:1﹣20%﹣50%=30%,故此选项正确;因为摸出黑球的频率稳定于50%,大于其它频率,所以②从布袋中任意摸出一个球,该球是黑球的概率最大,故此选项正确;③若再摸球100次,不一定有20次摸出的是红球,故此选项错误.故答案为:①②.
在对某次试验数据整理过程中,某个事件出现的频率随试验次数变化折线图如图所示,这个图形中折线的变化特点是______________________________,试举一个大致符合这个特点的实物试验的例子(指出关注的结果)_______________________________________.
随着试验次数增加,频率趋于稳定
如抛掷硬币试验中关注正面出现的频率
2.(2020•安顺)下列4个袋子中,装有除颜色外完全相同的10个小球,任意摸出一个球,摸到红球可能性最大的是( )A. B. C. D.
1.(2019•徐州)抛掷一枚质地均匀的硬币2000次,正面朝上的次数最有可能为( )A.500B.800C.1000D.1200
1.为了看图钉落地后钉尖着地的频率有多大,小明做了大量重复试验,发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )A.钉尖着地的频率是0.4B.随着试验次数的增加,钉尖着地的频率稳定在0.4附近C.前20次试验结束后,钉尖着地的次数一定是8次
2.在一个不透明的布袋中,红色、黑色、白色的球共有120个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在15%和45%,则口袋中白色球的个数很可能是( ) A.48个 B.60个 C.18个 D.54个
3. 一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( ) A.6 B.10 C.18 D.20
4.养鱼专业户为了估计他承包的鱼塘里有多少条鱼(假设这个塘里养的是同一种鱼),先捕上100条做上标记,然后放回塘里,过了一段时间,待带标记的鱼完全和塘里的鱼混合后,再捕上100条,发现其中带标记的鱼有10条,鱼塘里大约有鱼多少条?
解:设鱼塘里有鱼x条,根据题意可得
答:鱼塘里有鱼1000条.
在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球实验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)(2)若从盒子里随机摸出一只球,则摸到白球的频率的估计值为 ;(3)试估算盒子里黑、白两种颜色的球各有多少只?
解:盒子里白颜色的球有40×0.6=24(只),黑颜色的球有40﹣24=16 (只) .
小晨和小冰两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了100次实验,实验的结果如下:(1)计算“2点朝上”的频率和“3点朝上”的频率;(2)小晨说:“根据实验,一次实验中出现4点朝上的可能性是 ;”小晨的这一说法正确吗?为什么?
(3)小冰说:“根据实验,如果掷1000次,那么出现5点朝上的次数是200次.”小冰的这一说法正确吗?为什么?
解:(1)2点朝上出现的频率= ;3点朝上的频率= ;
(2)小晨的说法不正确,因为4点朝上的频率为 ,不能说明4点朝上这一事件发生的可能性就是 ,只有当实验的次数足够多时,该事件发生的频率才稳定在事件发生的可能性附近,才可以将这个频率的稳定值作为该事件发生的可能性.
(3)小冰的说法是不正确的,因为不确定事件发生具有随机性,所以5点朝上出现的次数不一定是200次.
频率:在n次重复试验中,事件A发生了m次,则 比值 称为事件A发生的频率.
初中数学北师大版七年级下册2 频率的稳定性课文内容ppt课件: 这是一份初中数学北师大版七年级下册2 频率的稳定性课文内容ppt课件,共33页。PPT课件主要包含了什么是频率,频率的稳定性等内容,欢迎下载使用。
初中数学北师大版七年级下册2 频率的稳定性说课课件ppt: 这是一份初中数学北师大版七年级下册2 频率的稳定性说课课件ppt,共31页。PPT课件主要包含了必然事件,不可能事件,随机事件,确定事件,看一看,议一议,数学史实等内容,欢迎下载使用。
北师大版七年级下册2 频率的稳定性优秀ppt课件: 这是一份北师大版七年级下册2 频率的稳定性优秀ppt课件,文件包含62频率的稳定性第1课时pptx、北师大版中学数学七年级下第六章概率初步62频率的稳定性第1课时教学详案docx、62频率的稳定性第1课时同步练习docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。













