七年级上册5.5 应用一元一次方程——“希望工程”义演课堂教学课件ppt

这是一份七年级上册5.5 应用一元一次方程——“希望工程”义演课堂教学课件ppt，共23页。PPT课件主要包含了课堂讲解，积分问题计费问题，课时流程，逐点导讲练，课堂小结，作业提升，知识点，积分问题，计费问题等内容，欢迎下载使用。

例1 在一次有12支队参加的足球循环赛(每两队之间赛且 只赛一场)中，规定胜一场记3分，平一场记1分，负 一场记0分．某队在这次循环赛中胜的场数比负的场 数多2场，结果共积18分，则该队平了几场？ 导引：由题可知，共12支队参赛，则每支队均赛11 场．设该队胜了x场，则负了(x－2)场，平了 11－x－(x－2)＝－2x＋13(场)．
解：设该队胜了x场，则负了(x－2)场， 平了11－x－(x－2)＝－2x＋13(场)． 由题意可得： 3x＋1×(－2x＋13)＝18，解得x＝5， －2x＋13＝3(场)． 答：该队平了3场．
例2 足球比赛的得分规则：胜一场得3分，平一场得1 分，负一场得0分．一支足球队在某个赛季共需 比赛14场．现已比赛8场，负了一场，共得17分． (1)前8场比赛中，这支球队胜了几场？ (2)这支球队打满14场，最高能得多少分？ (3)通过对比赛情况的分析，这支球队打满14场比赛， 得分不低于29分，就可达到目标．请你分析一下， 在后面的6场比赛中，这支球队至少要胜几场， 才能达到预期的目标？
解：(1)设这支球队胜了x场，则平了(8－1－x)场． 由题意，得3x＋(8－1－x)×1＝17， 解得x＝5. 答：前8场比赛中，这支球队胜了5场． (2)要使得分最高，必须在后面的几场比赛中全胜， 因此，打满14场比赛最高能得17＋(14－8)×3 ＝35(分)．
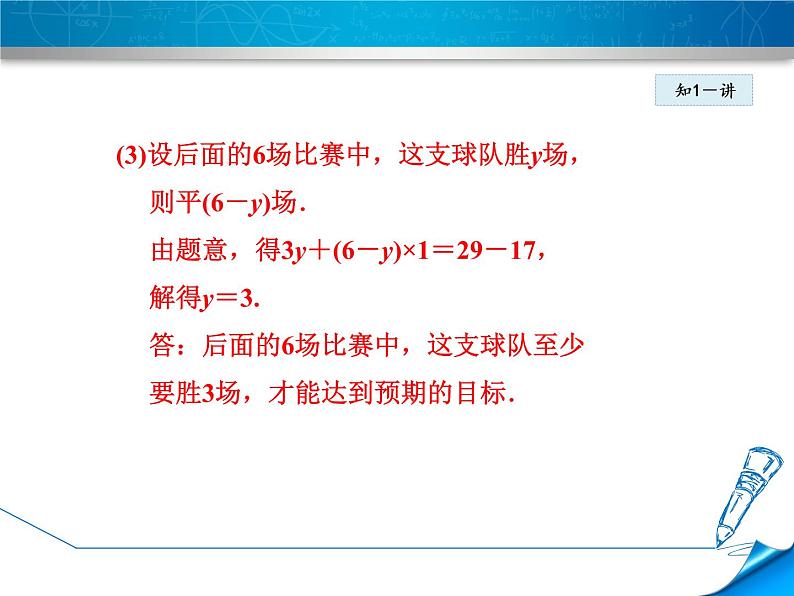
(3)设后面的6场比赛中，这支球队胜y场， 则平(6－y)场． 由题意，得3y＋(6－y)×1＝29－17， 解得y＝3. 答：后面的6场比赛中，这支球队至少 要胜3场，才能达到预期的目标．
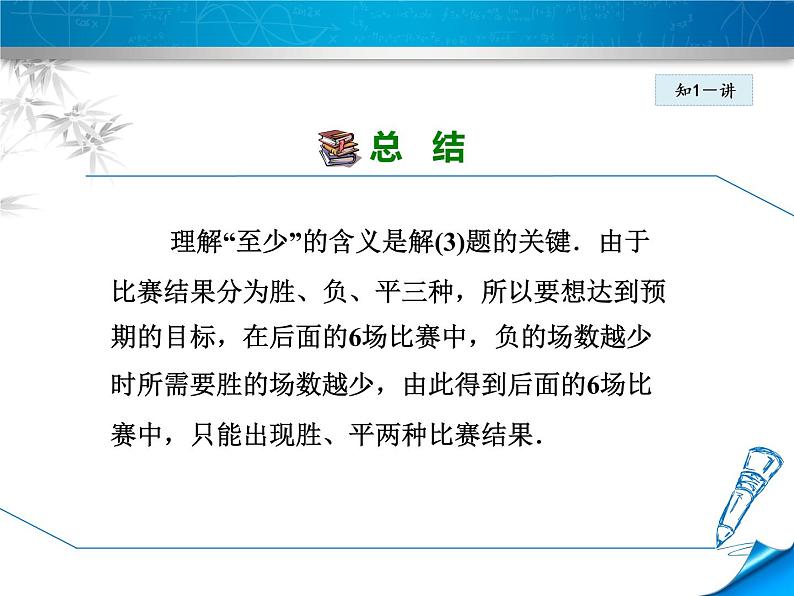
理解“至少”的含义是解(3)题的关键．由于比赛结果分为胜、负、平三种，所以要想达到预期的目标，在后面的6场比赛中，负的场数越少时所需要胜的场数越少，由此得到后面的6场比赛中，只能出现胜、平两种比赛结果．
李明是学校的篮球小明星，在一场篮球比赛中，他一人得了21分，如果他投进的2分球比3分球多3个，那么他一共投了(　　)个2分球．A．2 B．3 C．6 D．7
爸爸和儿子共下12盘棋(未出现平局)后，得分相同，爸爸赢一盘记1分，儿子赢一盘记2分，则爸爸赢了(　　)A．9盘 B．8盘 C．4盘 D．3盘
例3 某市上网有两种收费方案，用户可任选其一：A 为计时制——1元/h；B为包月制——80元/月， 此外每种上网方式都附加通讯费0.1元/h. (1)某用户每月上网40 h，选哪种方式比较合算？ (2)某用户每月有100元钱用于上网，选哪种方式 比较合算？ (3)请你设计一个方案，使用户能合理地选择上 网方式．
导引：(1)提供了上网时间40 h，根据“单价×总时 ＝总价”，求出A，B收费方案下的费用， 进行比较． (2)提供了上网的总费用，已知上网的单价， 求出总时长进行比较． (3)根据用户的上网时长，比较哪种方案收费 较少，帮其设计合理的方案．
解：(1)如果用户每月上网40 h， A计时制：40×(0.1＋1)＝44(元)， B包月制：80＋40×0.1＝84(元)， 44<84，故选A计时制比较合算． (2)设用户用100元上网，A计时制可上网x h， B包月制可上网y h， 则(1＋0.1)x＝100， 解得x＝ ≈91，
80＋0.1y＝100，解得y＝200. 91<200，故选B包月制比较合算．(3)设用户上网z h，两种方式收费一样多． 则(1＋0.1)z＝80＋0.1z. 解得z＝80. 故上网不足80 h，选A计时制； 上网超过80 h，选B包月制； 上网恰好80 h，两种方案都一样．
例4 某旅行社拟在暑假期间面向学生推出“林州红旗渠 一日游”活动．收费标准如下：
甲、乙两所学校计划组织本校学生自愿参加此项活动．已知甲校报名参加的学生人数多于100人，乙校报名参加的学生人数少于100人．
经核算，若两校分别组团共需花费20 800元， 若两校联合组团只需花费18 000元．(1)两所学校报名参加旅游的学生人数之和是多少？(2)两所学校报名参加旅游的学生各有多少人？
解：(1)设两所学校报名参加旅游的学生人数之和为x人． 若两所学校报名参加旅游的学生人数之和多于200 人，则x＝18 000÷75＝240. 若两所学校报名参加旅 游的学生人数之和在100人 到200人(包括200人)之间，
则x＝18 000÷85＝211 ，不合题意，舍去． 所以两所学校报名参加旅游的学生人数之和是240人．(2)设甲学校报名参加旅游的学生有y人， 则乙学校报名参加旅游的学生有(240－y)人． 当甲学校学生人数在100人到200人(包括200人)之间时， 根据题意，得85y＋90(240－y)＝20 800， 解得y＝160. 则240－y＝240－160＝80.
当甲学校学生人数多于200人时，根据题意，得75y＋90(240－y)＝20 800.解得y＝53 ，不合题意，舍去．综上所述，甲学校报名参加旅游的学生有160人，乙学校报名参加旅游的学生有80人．
本题容易出现的错误是分类时出现漏解，如只考虑到甲校报名参加旅游的学生人数多于100人，漏掉了甲校报名参加旅游的学生人数多于200人的情况，或漏掉了两所学校报名参加旅游的学生人数之和在100人到200人(包括200人)之间的情况．
有一旅客带30 kg行李从北京到广州，按民航规定，旅客最多可免费携带20 kg行李，超过部分每千克按飞机票价的1.5%购买行李票，已知该旅客购买的行李票为180元，则他的飞机票价为(　　)A．800元 B．1 000元C．1 200元 D．1 400元
某种出租车的收费标准是：起步价7元(即行驶距离不超过3千米都需付7元车费)，超过3千米后，每增加1千米，加收2.4元(不足1千米按1千米计算)．某人乘这种出租车从甲地到乙地共付车费19元，设此人从甲地到乙地经过的路程是x千米，那么x的最大值是(　　)A．11 B．8 C．7 D．5
积分问题这类问题中的基本关系有：(1)比赛总场数=胜场数+负场数+平场数；(2)比赛总积分=胜场积分+负场积分+平场积分.
分段收费是随市场经济改革应运而生的一种科学、规范、合理的收费方式．现在许多部门的相关行业都制定了相应的分段收费标准．相等关系：第一段费用＋第二段费用＋…＝总费用．常见的分段收费：水费，电费，煤气费，个人所得税，打折销售等．