初中数学人教版八年级上册第十四章 整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方教课ppt课件

这是一份初中数学人教版八年级上册第十四章 整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方教课ppt课件，共21页。PPT课件主要包含了教学目标，教学重点，一课前检测，12函数，时间t，路程S，二设疑自学，请填写下表，L10+05m，问题3等内容，欢迎下载使用。
正确理解函数的定义并会解决实际问题
理解函数概念，并能根据具体问题列出函数关系式。
教学难点实际问题中的自变量的取值范围。
1.什么叫变量？2.什么叫常量？
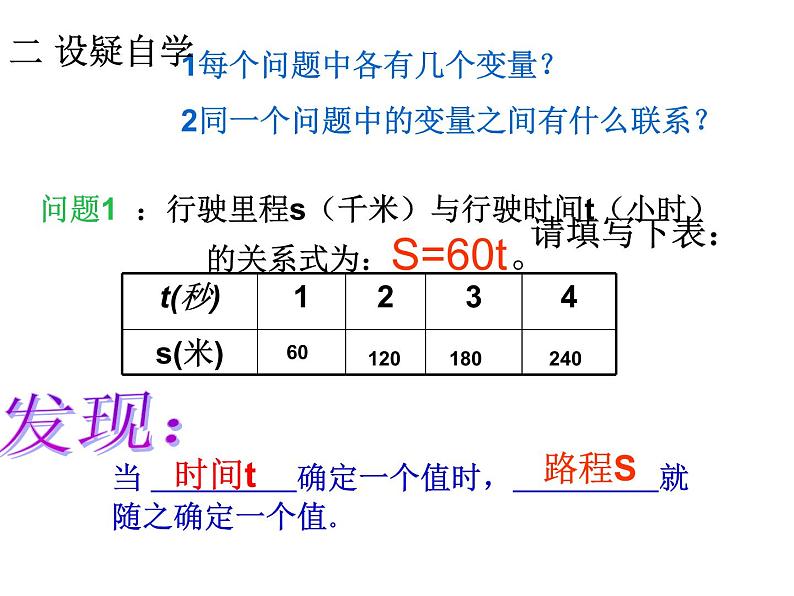
问题1 ：行驶里程s（千米）与行驶时间t（小时）的关系式为：S=60t。
当 确定一个值时， 就随之确定一个值。
1每个问题中各有几个变量？ 2同一个问题中的变量之间有什么联系？
三 展示交流 票房收入y元与售票数量x张的关系式： y=10x X=150时 y=1500; X=205时 y=2050；
当________确定一个值时，_______就随之确定一个值。
用含重物质量m（kg）的式子表示受力后的弹簧长度 L(cm)为：
当 确定一个值时，———— 就随之确定一个值。
问题4 圆的半径r 与圆的面积s的关系式：计算： S=10 时，r=＿ ＿ ＿ cm S=20 时，r= ＿ ＿ ＿ cm
当 _____确定一个值时，_____随之就确定一个值。
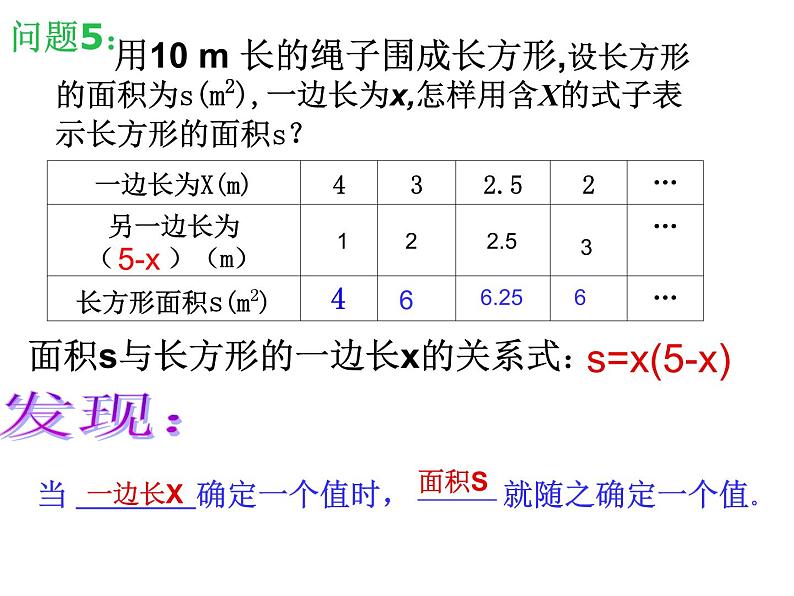
用10 m 长的绳子围成长方形,设长方形的面积为s(m2),一边长为x,怎样用含X的式子表示长方形的面积s？
当 确定一个值时， ———— 就随之确定一个值。
面积s与长方形的一边长x的关系式：
2 两个变量互相联系，当其中一个 变量确定一个值时，另一个变量也（ ）。
1 每个变化的过程中都存在着（ ）变量.
（1）下图是体检时的心电图．其中图上点的横坐标x表示时间，纵坐标y表示心脏部位的生物电流，它们是两个变量．在心电图中，对于x的每一个确定的值，y都有唯一确定的对应值吗？
（2）在下面的我国人口数统计表中，年份与人口数 可以记作两个变量x与y，对于表中每一个确定的年份（x），都对应着一个确定的人口数（y）吗？
如果当x=a时y=b，那么b叫做当自变量的值为a时的函数值。
思考： 上面五个问题中哪些是自变量,哪些是自变 量的函数？
如果有两个变量x与y,
并且对于x的每一个确定的值，y都有唯 一确定的值与其对应，
那么我们就说x是自变量 ，
（1）在计算器上按照下面的程序进行操作：
问题：显示的数y是x的函数吗？为什么?
y是x的函数，因为x取定一个值时，y都有唯一确定的值与其对应。
y是X的函数吗？若是，写出它的表达式（用含X的式子表示y).
例1 一辆汽车的油箱中现有汽油50L，如果不再加油，那么油箱中的油量y（单位：L）随行驶里程x（单位：km）的增加而减少，平均耗油量为0.1L/km。
（1）写出表示y与x的函数关系的式子。
（2）指出自变量x的取值范围；
（3）汽车行驶200 km时，油箱中还有多少油？
解:(1) 函数关系式为: y = 50－0.1x
(2) 由x≥0及0.1x ≤ 50　得　0 ≤ x ≤ 500∴自变量的取值范围是: 0 ≤ x ≤ 500
(3)把x = 200代入 y =50 －0.1x得 :
因此,当汽车行驶200 km时,油箱中还有油30L。
这样的式子叫做函数解析式。
y=50-0.1×200=30
注意： 确定自变量的取值范围时，不仅要考虑函数关系式有意义，而且还要注意问题的实际意义。
对于x的每一个值，y总有唯一的值与它对应，y才是x的函数。
解:1 y是x的函数。 2、y是x的函数。 ∵X-3 ≥0∴x ≥3. 3、y不是x的函数。 4、y是x的函数. x≠0.
1,二次根号下的式子≥02,分母中的式子不能为03,其他时候为任意实数4,实际应用中考虑实际意义.
2.下列问题中哪些量是自变量？哪些量是自变量的函数?试写出用自变量表示函数的式子。
（1）改变正方形的边长X，正方形的面积S随之改变。
（2）秀水村的耕地面积是106 ,这个村人均占有耕地面积y随这个村人数n的变化而变化。
____是自变量，___ 是___的函数，
关系式__________。
___是自变量，___是___的函数，
关系式____________。