数学八年级上册6 实数完美版课件ppt

这是一份数学八年级上册6 实数完美版课件ppt，共29页。PPT课件主要包含了学习目标，数学危机，有理数，无理数，叫做无理数，无限不循环小数，1按定义分，正实数，负实数，负有理数等内容，欢迎下载使用。

1.了解实数的意义，能对实数按要求分类.(重点）2.了解实数范围内相关概念的意义.(重点）3.了解实数与数轴上点的一一对应关系.能用数轴上 的点表示无理数.(难点）
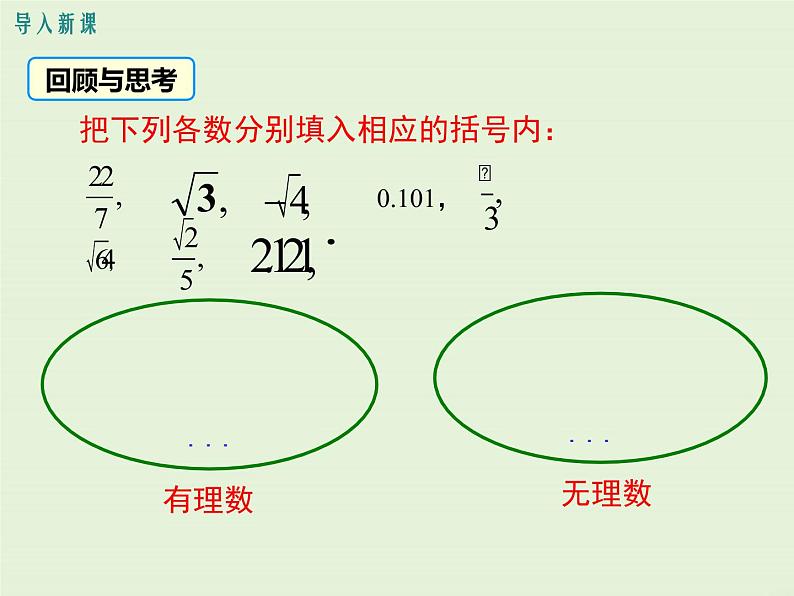
把下列各数分别填入相应的括号内：
问题1 我们知道有理数包括整数和分数，利用计算器把下列分数写成小数的形式，它们有什么特征？
它们都可以化成有限小数或无限循环小数的形式
问题2 整数能写成小数的形式吗？3可以看成是3.0吗？
思考 由此你可以得到什么结论？
有理数都可以化成有限小数或无限循环小数的形式.
反过来，任何有限小数或无限循环小数的也都是有理数.
想一想：所有的数都可以写成有限小数和无限循环小数的形式吗？如：
π=3.1415926535897932384626…
1.01001000100001…
它们都是无限不循环小数，是无理数
思考：我们将有理数和无理数统称为实数，仿照有 理数的分类吗？据此你能给实数分类吗？
无理数：无限不循环小数
有理数：有限小数或无限循环小数
你能分辩下列各数是哪个家庭的成员吗?试试看？
在实数范围内 ，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样．例如：
与 互为相反数
问题：在有理数范围内，能进行哪些运算？
有理数的运算及运算律对实数仍然适用
例1：分别求下列各数的相反数、倒数和绝对值．
解：(1)∵ ＝－4，∴ 的相反数是4，倒数是 ，绝对值是4.(2)∵ ＝15，∴ 的相反数是－15，倒数是 ，绝对值是15.(3) 的相反数是－ ，倒数是 ，绝对值是 .
（1）a是一个实数，它的相反数为 ， 绝对值为 ；
（2）如果a ≠0，那么它的倒数为 .
思考1： 如图，直径为１个单位长度的圆从原点沿数轴向右滚动一周，圆上一点从原点到达A点，则数轴上表示点A的数是多少？
因为圆的周长为π,无理数π可以用数轴上的点来表示.
提醒：播放状态下点击画面操作
把两个边长为1的小正方形通过剪、拼，得到一个大正方形，大正方形的边长为 ，从而说明边长为1的小正方形的对角线为 .
每一个实数都可以用数轴上的一个点来表示；
反过来，数轴上的每一点都表示一个实数.
★实数和数轴上的点是一一对应的.
视频：在数轴上表示 和π
例2：如图所示，数轴上A，B两点表示的数分别为－1和 ，点B关于点A的对称点为C，求点C所表示的实数．
解：∵数轴上A，B两点表示的数分别为－1和 ，∴点B到点A的距离为1＋ ，则点C到点A的距离为1＋ ，设点C表示的实数为x，则点A到点C的距离为－1－x，∴－1－x＝1＋ ，∴x＝－2－
本题主要考查了实数与数轴之间的对应关系，其中利用了：当点C为点B关于点A的对称点时，点C到点A的距离等于点B到点A的距离；两点之间的距离为两数差的绝对值．
例3：如图所示，数轴上A，B两点表示的数分别为 和5.1，则A，B两点之间表示整数的点共有(　　)A．6个 B．5个 C．4个 D．3个
【方法总结】数轴上的点与实数一一对应，结合数轴分析，可轻松得出结论．
①实数不是有理数就是无理数.（ ）
③无理数都是无限小数.（ ）
④带根号的数都是无理数.（ ）
⑤无理数一定都带根号.（ ）
⑥两个无理数之积不一定是无理数.（ ）
⑦两个无理数之和一定是无理数.（ ）
⑧数轴上的任何一点都可以表示实数.（ ）
②无理数都是无限不循环小数.（ ）
2.把下列各数填入相应的集合内：
3.在 -3，－ ， －1， 0 这四个实数中，最大的是（ ） A. -3 B.－ C. －1 D. 0
4.如图，在数轴上点A和点B之间的整数是 ．
【解析】1＜ ＜2，2＜ ＜3， 在 与 之间的整数是2.
5. 实数 a,b 的位置如图 化简 |a + b| – |a – b|
解:由数轴可知，a+b<0，a－b<0，从而 原式=－(a＋b)－[－（a－b）] = －a－b＋（a－b） = －a－b＋（a－b） = －a－b＋a－b = －2b