北师大版八年级上册第二章 实数6 实数精品ppt课件

这是一份北师大版八年级上册第二章 实数6 实数精品ppt课件，共33页。PPT课件主要包含了知识回顾，有理数，正有理数，负有理数，导入新知，素养目标，探究新知，按定义分，女孩子，男孩子等内容，欢迎下载使用。

1.什么是有理数？有理数怎样分类？
2.什么是无理数？带根号的数都是无理数吗？
无理数是无限不循环小数.带根号的数不一定是无理数.
1. 了解实数的意义，并能将实数按要求进行准确的分类.
2. 了解实数范围内相关概念的意义.
3. 了解实数和数轴上的点一一对应，能用数轴上的点表示无理数.
（1）请把下列有理数写成小数的形式，你有什么发现？任何有理数都能写成有限小数和无限循环小数吗？（2）请用计算器把 和 写成小数的形式，你有什么发现？像这样的数我们把它叫什么数？你还能说出一些这样的数吗？
事实上，任何一个有理数都可以写成有限小数或无限循环小数.
反过来，任何有限小数或无限循环小数也都是有理数.
无限不循环的小数 ---------- 叫做无理数.
你能举出一些无理数吗？
0.1010010001…〔两个1之间依次多1个0〕
－168.3232232223…〔两个3之间依次多1个2〕
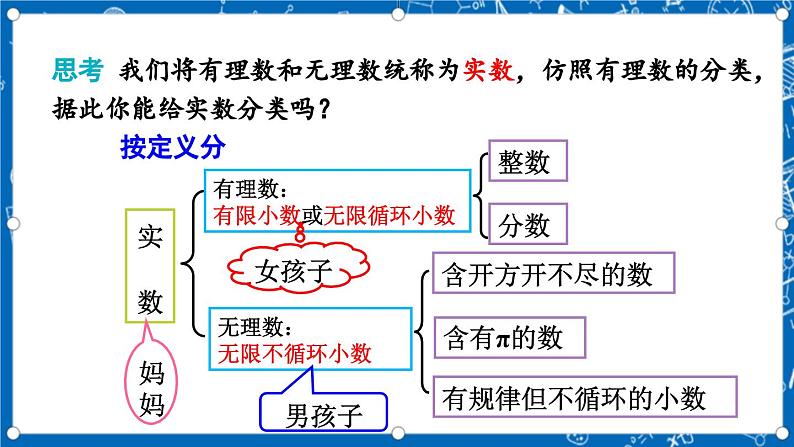
思考 我们将有理数和无理数统称为实数，仿照有理数的分类，据此你能给实数分类吗？
无理数：无限不循环小数
有理数：有限小数或无限循环小数
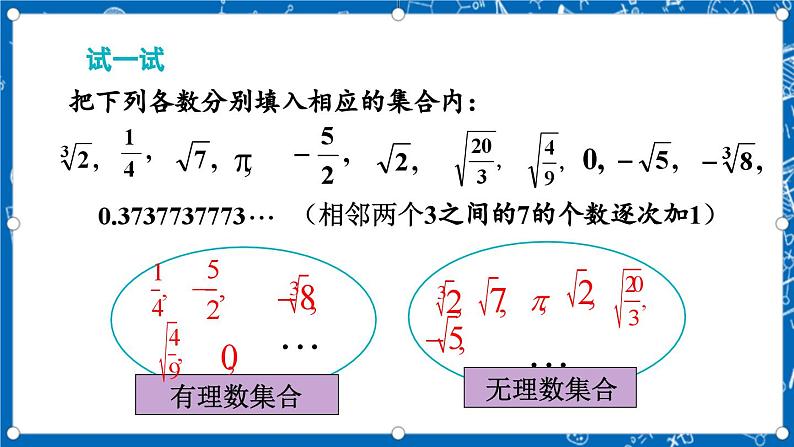
把下列各数分别填入相应的集合内：
无理数和有理数一样，也有正负之分.
1.你能把下列各数分别填入相应的集合内吗?
2. 0属于正数吗?属于负数吗?
3. 实数还可以怎样分类?
例1 将下列各数分别填入下列相应的括号内：
把下列各数填入相应的集合内：
提示1：在实数范围内 ，相反数、倒数、绝对值的意义和有理数范围内 的相反数、倒数、绝对值的意义完全相同.
1.5的相反数是（ ），绝对值是（ ）,倒数是（ ）.
-1.5
（1） a 是一个实数 ，它的相反数为-a.
提示2：有理数的运算法则及运算律对实数仍然适用.
例 分别求下列各数的相反数、倒数和绝对值．
(1)正实数的绝对值是 ，0的绝对值是 ，负实数的绝对值是　 .
如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点从原点到达A点，则点A的坐标为多少？
问题1 无理数能在数轴上表示出来吗？

（3）如果将所有有理数都标到数轴上，那么数轴能填满吗？
在数轴上表示的两个实数，右边的数总比左边的数大.
数轴上的点有些表示有理数，有些表示无理数.
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数.即实数和数轴上的点是一一对应的.
解：因为数轴上A，B两点表示的数分别为-1和 ，所以点B到点A的距离为1＋ ，则点C到点A的距离为1+ ，设点C表示的实数为x，则点A到点C的距离为-1-x，所以-1-x＝1＋ ，所以x＝-2- .
1.如果以2为边长画一个正方形，以原点为圆心，正方形的对角线为半径画弧，与正半轴的交点就表示______，与负半轴的交点就表示________. 2.请将图中数轴上标有字母的各点与下列实数对应起来： ，-1.5， ， ，3解：点A、B、C、D、E分别对应_____、 ___、___、___、___.
如图，A，B，C，D是数轴上的四个点，其中最适合表示无理数π的点是（　　）A．点A B．点B C．点C D．点D
（1）实数不是有理数就是无理数. （ ）
（2）无理数都是无限不循环小数. （ ）
（4）无理数都是无限小数. （ ）
（3）带根号的数都是无理数. （ ）
（5）无理数一定都带根号. （ ）
3.求下列各数的相反数、倒数和绝对值:
比较下列各组数的大小：
解 ：（1）因为 12 < 42， 所以 －1< 3；
（2）因为 10 > 32 ， 所以
实数范围内的相关的概念
有理数和无理数统称实数