北师大版八年级上册第二章 实数6 实数授课ppt课件

这是一份北师大版八年级上册第二章 实数6 实数授课ppt课件，共19页。PPT课件主要包含了有理数，正有理数，负有理数，无理数，正无理数，负无理数，正整数，负整数，正分数，负分数等内容，欢迎下载使用。

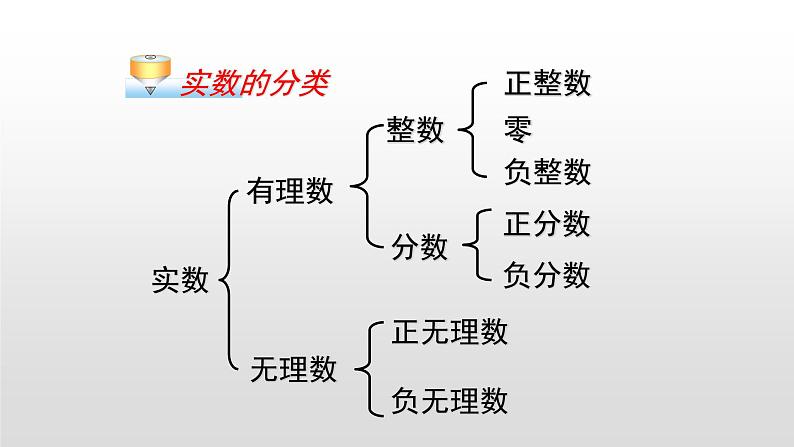
1.什么是有理数？有理数怎样分类？
无理数是无限不循环小数.带根号的数不一定是无理数.
2.什么是无理数？带根号的数都是无理数吗？
1.把下列各数分别填入相应的集合内.
你能把下面各数填入下面相应的集合内吗？
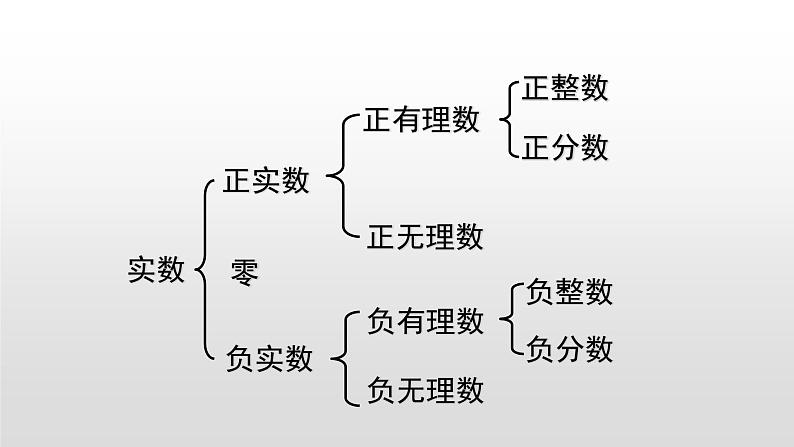
无理数和有理数一样,也有正负之分，如是正的,-π是负的.
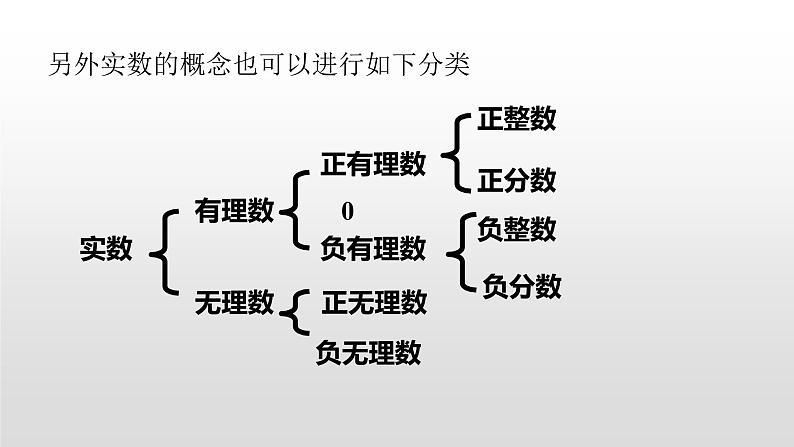
另外实数的概念也可以进行如下分类
在实数范围内 ，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.
与 互为相反数
练习：分别求下列各数的相反数、倒数和绝对值。
（2 ） 的相反数是
（1）∵ =-4，
∴ 的相反数是 ，
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则和运算律对实数仍然适用.
（1） a 是一个实数 ，它的相反数为 ？
（2） 如果 a ≠ 0 ，那么它的倒数为 .
(3) ︳a ︳=　　　　　　　　　　　　　　
（1）如图,OA=OB，数轴上的点A对应的数是什么？ 它介于哪两个整数之间？
（2）你能在坐标轴上找到 对应的点吗？
如图类似，OB为两直角边分别为1和2的直角三角形的斜边.
问题 :你能在数轴上找到表示元和√2及-√2这样的无理数的点吗?
每一个实数都可以用数轴上的一个点来表示.
数轴上的每一个点都表示一个实数.
每一个实数都可以用数轴上的一个点来表示;反过来，数轴上的每一个点都表示一个实数.即实数和数轴上的点是一一对应的.
在数轴上，右边的点表示的数比左边的点表示的数大.
①实数不是有理数就是无理数。（ ）
③无理数都是无限小数。（ ）
④带根号的数都是无理数。（ ）
⑤无理数一定都带根号。（ ）
⑥两个无理数之积不一定是无理数。（ ）
⑦两个无理数之和一定是无理数。（ ）
⑧数轴上的任何一点都可以表示实数。（ ）
②无理数都是无限不循环小数。（ ）
1. 的相反数是 .
2. 的倒数是 . 的倒数是 .
3.|-5|= , = .
4.|-π|= ， = .
习题2.8 1，2，3，4