人教版八年级上册第十一章 三角形11.3 多边形及其内角和11.3.2 多边形的内角和评课ppt课件

这是一份人教版八年级上册第十一章 三角形11.3 多边形及其内角和11.3.2 多边形的内角和评课ppt课件，共19页。PPT课件主要包含了多边形的内角和，学习目标，讲授新知，多边形的外角和，课堂小结，随堂测试等内容，欢迎下载使用。

1、理解多边形的内角和定理。2、能计算多边形的内角和。3、理解多边形的外角的定义和外角和定理。
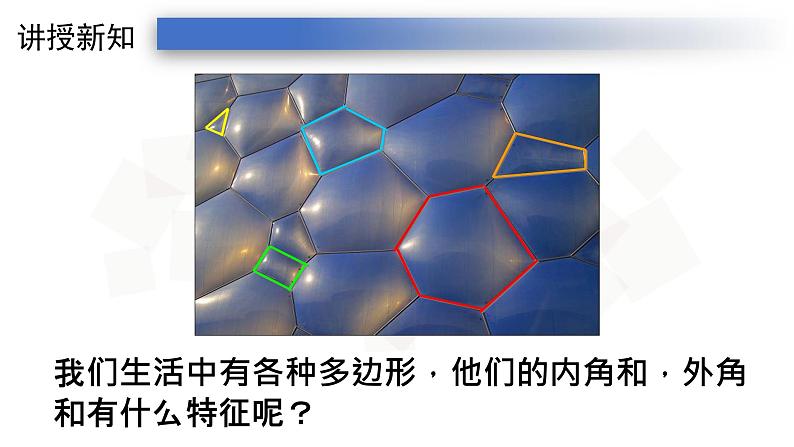
我们生活中有各种多边形，他们的内角和，外角和有什么特征呢？
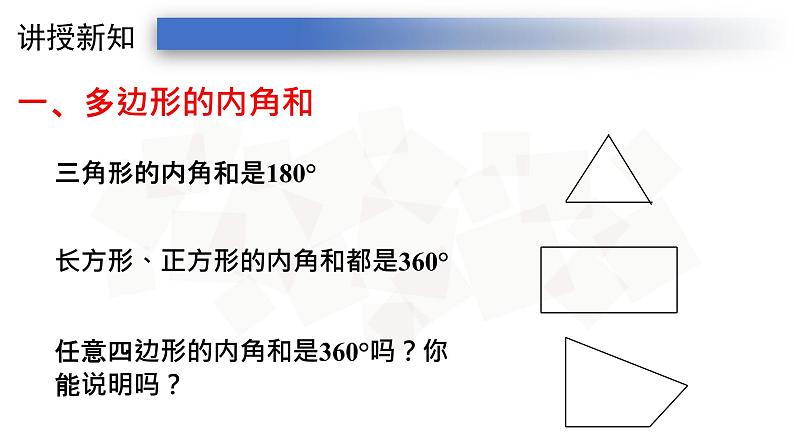
长方形、正方形的内角和都是360°
任意四边形的内角和是360°吗？你能说明吗？
三角形的内角和是180°
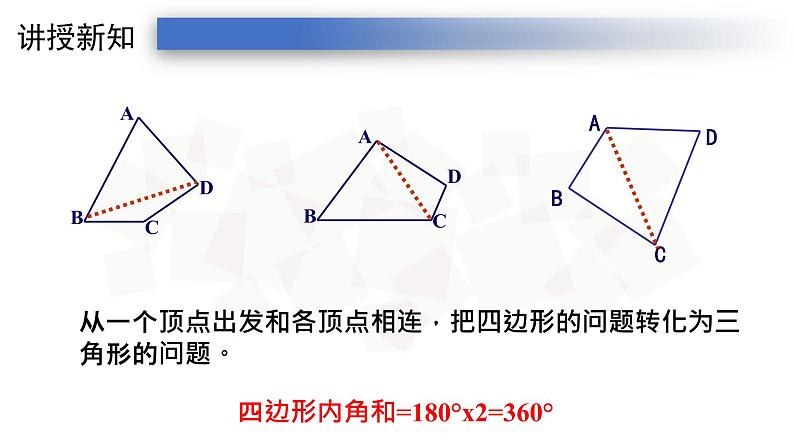
从一个顶点出发和各顶点相连，把四边形的问题转化为三角形的问题。
四边形内角和=180°x2=360°
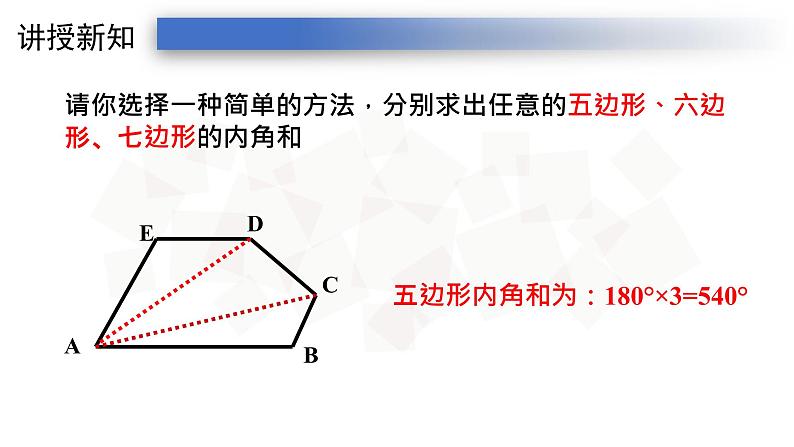
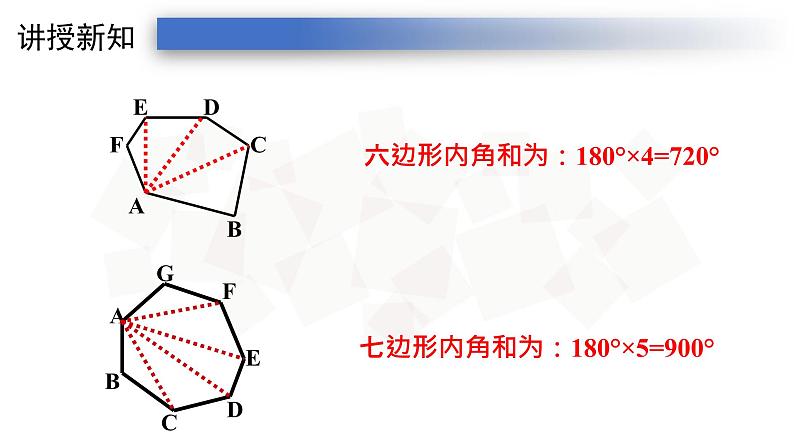
请你选择一种简单的方法，分别求出任意的五边形、六边形、七边形的内角和
五边形内角和为：180°×3=540°
六边形内角和为：180°×4=720°
七边形内角和为：180°×5=900°
综上，就得出了多边形的内角和公式：n边形的内角和等于(n－2)·180°(n>=3)
外角和：在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和.
外角：多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。
三角形的外角和是怎样探究出来的？1.先求3个外角+3个内角的和；2.再减去3个内角的和三角形的外角和=3×180 - (3-2)×180°=360°
1.4个外角+4个内角=4个平角= 360°2.再减去四个内角的和四边形的外角和 =4×180°- (4-2)×180°= 360°
1.求5个外角+5个内角的和2.再减去5个内角的和五边形的外角和 =5×180°-(5-2)×180°=360°
综上，n边形的外角和：n×180°- (n-2) × 180°= 360 ° 即任意多边形的外角和都等于360°.
一、多边形的内角和多边形的内角和公式：n边形的内角和等于(n－2)·180°(n>=3)二、多边形的外角1.外角：多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角。2.外角和：在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和。三、多边形的外角和n边形的外角和：n×180°- (n-2) × 180°= 360 °即任意多边形的外角和都等于360°.
1.十五边形的外角和为_____
2.已知一个多边形的每一个外角都是60°，这个多边形的边数为______
3.如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____
4.一个多边形的外角和是内角和的一半，则它的边数是（ ） A.7 B.6 C.5 D.45.如果一个正多边形的一个内角等于140°,则这个多边形的边数是（ ） A.12 B.9 C. 8 D.7
6.求下列图形中的X的值：
解：120。+150。+90。+ x。+2x。=180。×（5-2） 360。+3x。=540。 3x。=180。 x。=60。
解：140。+90。+x。+x。=180。×（4-2） 230。+2x。=360。 2x。= 130。 x。=65。
7.已知一个多边形，它的内角和等于五边形的内角和的2倍，求这个多边形的边数．
解：设边数为n，则可列方程为：
(n - 2) ×180°=（5 - 2）×180°× 2解得 n = 8所以这个多边形的边数是八。