初中数学人教版八年级上册14.2.2 完全平方公式优质ppt课件

这是一份初中数学人教版八年级上册14.2.2 完全平方公式优质ppt课件，共30页。PPT课件主要包含了你发现了什么，完全平方公式，p2+2p+1，m2+4m+4，p2–2p+1，m2–4m+4，a2+2ab+b2，a2–2ab+b2，问题1，问题2等内容，欢迎下载使用。

一块边长为a米的正方形实验田，因实际需要将其边长增加b米，形成四块实验田，以种植不同的新品种.(如图)用不同的形式表示实验田的总面积，并进行比较.你有什么发现呢？
2. 灵活应用完全平方公式进行计算.
1. 理解并掌握完全平方公式的推导过程、结构特点、几何解释.
3. 体验归纳添括号法则.
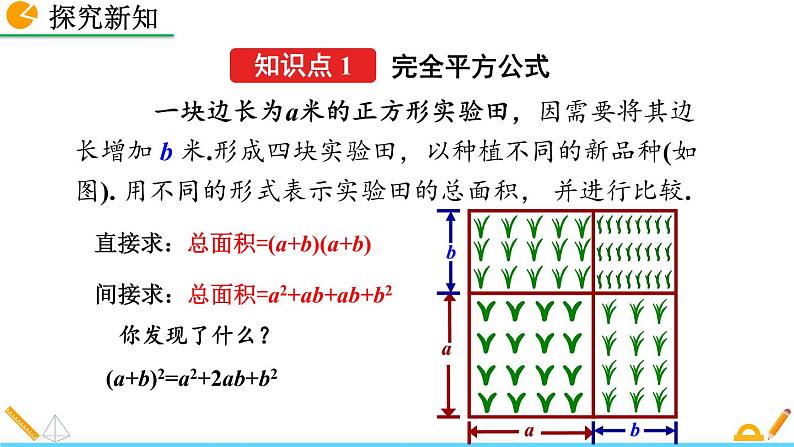
一块边长为a米的正方形实验田，因需要将其边长增加 b 米.形成四块实验田，以种植不同的新品种(如图). 用不同的形式表示实验田的总面积， 并进行比较.
直接求：总面积=(a+b)(a+b)
间接求：总面积=a2+ab+ab+b2
(a+b)2=a2+2ab+b2
计算下列多项式的积，你能发现什么规律？
(1) (p+1)2=(p+1)(p+1)= .
(2) (m+2)2=(m+2)(m+2)= .
(3) (p–1)2=(p–1)(p–1)= .
(4) (m–2)2=(m–2)(m–2)= .
根据你发现的规律，你能写出下列式子的答案吗？
(a+b)2= .
(a–b)2= .
也就是说，两个数的和(或差)的平方，等于它们的平方和，加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
简记为：“首平方，尾平方，积的2倍放中央”
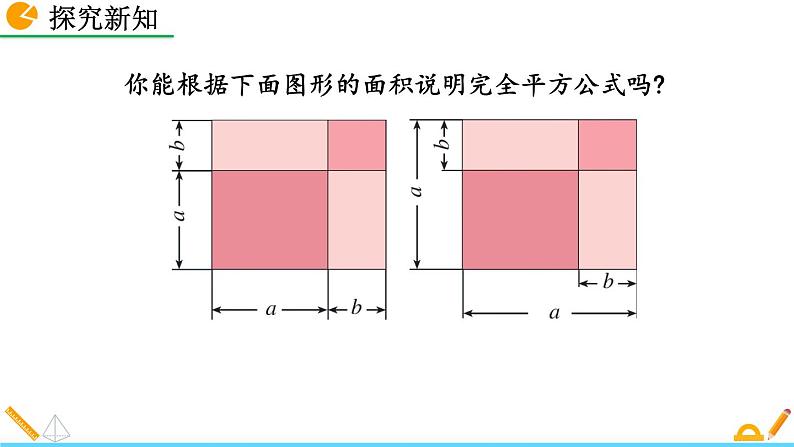
你能根据下面图形的面积说明完全平方公式吗?
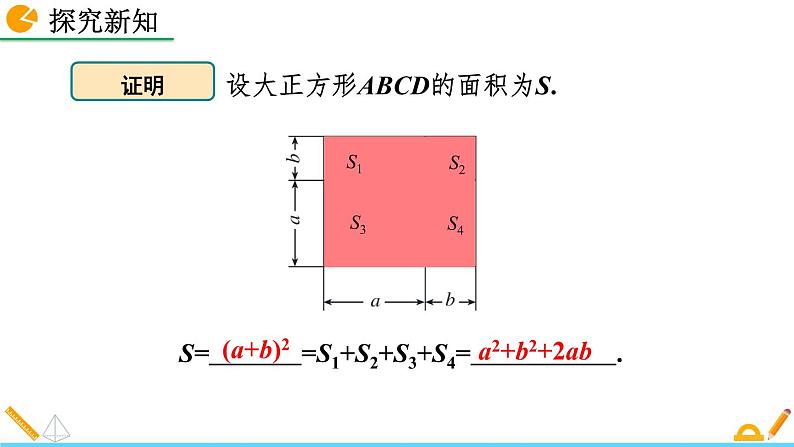
设大正方形ABCD的面积为S.
S= =S1+S2+S3+S4= .
a2−2ab+b2 .
(a+b)2= a2+2ab+b2.
(a–b)2= a2–2ab+b2.
观察下面两个完全平方式，比一比，回答下列问题：
(1) 说一说积的次数和项数.
(2) 两个完全平方式的积有相同的项吗？与a，b有什么关系？
(3) 两个完全平方式的积中不同的是哪一项？与a， b有什么关系？它的符号与什么有关？
公式中的字母a，b可以表示数、单项式和多项式.
积中两项为两数的平方和；
另一项是两数积的2倍，且与两数中间的符号相同.
下面各式的计算是否正确？如果不正确，应当怎样改正？
(1)(x+y)2=x2 +y2
(2)(x –y)2 =x2 –y2
(3) (–x +y)2 =x2+2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2
(x +y)2 =x2+2xy +y2
(x –y)2 =x2 –2xy +y2
(–x +y)2 =x2 –2xy +y2
(2x +y)2 =4x2+4xy +y2
例1 运用完全平方公式计算：
解: (4m+n)2=
(1)(4m+n)2；
(a + b)2= a2 + 2ab + b2
利用完全平方公式进行计算
(a – b)2 = a2– 2ab + b2
解： =
1. 利用完全平方公式计算：(1)(5–a)2； (2)(–3m–4n)2；(3)(–3a＋b)2.
(3)(–3a＋b)2＝9a2–6ab＋b2.
解：(1)(5–a)2＝25–10a＋a2；
(2)(–3m–4n)2＝9m2＋24mn＋16n2；
= (100 –1)2
=10000 –200+1
=10000+400+4
例2 运用完全平方公式计算：
利用完全平方公式进行简便计算
2. 利用乘法公式计算：(1)982–101×99； (2)20162–2016×4030＋20152.
＝(2016–2015)2＝1.
解：(1)原式＝(100–2)2–(100＋1)(100–1)
＝1002–400＋4–1002＋1＝–395；
(2)原式＝20162–2×2016×2015＋20152
例3 已知x–y＝6，xy＝–8.求:(1) x2＋y2的值； (2)(x+y)2的值.
＝36 –16＝20；
解：(1)∵x–y＝6，xy＝–8，
(x–y)2＝x2＋y2–2xy，
∴x2＋y2＝(x–y)2＋2xy
(2)∵x2＋y2＝20，xy＝–8，
∴(x+y)2＝x2＋y2＋2xy
利用完全平方公式的变形求整式的值
方法总结：本题要熟练掌握完全平方公式的变式：x2＋y2＝(x–y)2＋2xy＝(x+y)2–2xy，(x–y)2＝(x+y)2–4xy.
(1)已知x+y=10，xy=24，则x2+y2=_____.
(2)如果x2+kx+81是运用完全平方式得到的结果， 则k=________ .
(3)已知ab=2，(a+b)2=9，则(a–b)2的值为______.
a+(b+c) = a+b+c; a– (b+c) = a – b – c.
a + b + c = a + ( b + c) ; a – b – c = a – ( b + c ) .
把上面两个等式的左右两边反过来，也就是添括号：
添括号时，如果括号前面是正号，括到括号里的各项都不变号;如果括号前面是负号，括到括号里的各项都改变符号(简记为“负变正不变”).
例4 运用乘法公式计算:(1) (x+2y–3)(x–2y+3) ; (2) (a+b+c)2.
(2)原式= [(a+b)+c]2
= x2–(2y–3)2
= x2–(4y2–12y+9)
= x2–4y2+12y–9.
= (a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2.
4. 计算：(1)(a–b＋c)2； (2)(1–2x＋y)(1＋2x–y)．
＝1–4x2＋4xy–y2.
解：(1)原式＝[(a–b)＋c]2
＝(a–b)2＋c2＋2(a–b)c
＝a2–2ab＋b2＋c2＋2ac–2bc；
(2)原式＝[1＋(–2x＋y)][1–(–2x＋y)]
＝12–(–2x＋y)2
1. 将9.52变形正确的是(　　) A．9.52=92+0.52 B．9.52=(10+0.5)(10–0.5) C．9.52=102–2×10×0.5+0.52 D．9.52=92+9×0.5+0.52
2. 若x2+2(m–3)x+16是关于x的完全平方式，则m=　 ．
2.下列计算结果为2ab–a2–b2的是( ) A．(a–b)2 B．(–a–b)2 C．–(a＋b)2 D．–(a–b)2
1. 运用乘法公式计算(a–2)2的结果是(　　) A．a2–4a+4 B．a2–2a+4 C．a2–4 D．a2–4a–4
3.运用完全平方公式计算:
(1) (6a+5b)2=_______________；(2) (4x–3y)2=_______________ ；(3) (2m–1)2 =_______________；(4)(–2m–1)2 =_______________.
36a2+60ab+25b2
16x2–24xy+9y2
4.由完全平方公式可知：32＋2×3×5＋52＝(3＋5)2＝64，运用这一方法计算：4.3212＋8.642×0.679＋0.6792＝________．
计算:(1)(3a＋b–2)(3a–b＋2)；(2)(x–y–m＋n)(x–y＋m–n)．
(2)原式＝[(x–y)–(m–n)][(x–y)＋(m–n)]
解：(1)原式＝[3a＋(b–2)][3a–(b–2)]
＝(3a)2–(b–2)2
＝9a2–b2＋4b–4.　
＝(x–y)2–(m–n)2
＝x2–2xy＋y2–m2＋2mn–n2.
1.若a+b=5，ab=–6， 求a2+b2，a2–ab+b2.2.已知x+y=8，x–y=4，求xy.
解：a2+b2=(a+b)2–2ab=52–2×(–6)=37；
a2–ab+b2=a2+b2–ab=37–(–6)=43.
解：∵x+y=8， ∴(x+y)2=64，即x2+y2+2xy=64①;
∵x–y=4， ∴(x–y)2=16，即x2+y2–2xy=16②;
(a±b)2= a2±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子，可能需要先添括号变形成符合公式的要求才行
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
a2+b2=(a+b)2–2ab=(a–b)2+2ab; 4ab=(a+b)2–(a–b)2.