数学八年级上册13.3.1 等腰三角形集体备课课件ppt

这是一份数学八年级上册13.3.1 等腰三角形集体备课课件ppt，共17页。PPT课件主要包含了相关概念，认识等腰三角形，用符号语言表示为，活动5反馈练习，摩拳擦掌，等边对等角等内容，欢迎下载使用。

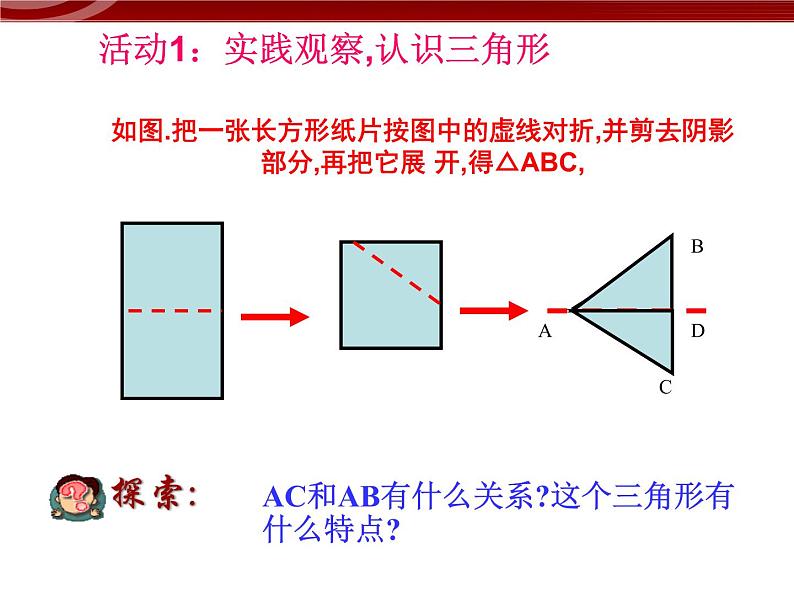
如图.把一张长方形纸片按图中的虚线对折,并剪去阴影部分,再把它展 开,得△ABC,
活动1：实践观察,认识三角形
定义：两条边相等的三角形叫做等腰三角形。
边：等腰三角形中,相等的两条边叫做腰，
　　　　　　　另一条边叫做底边.
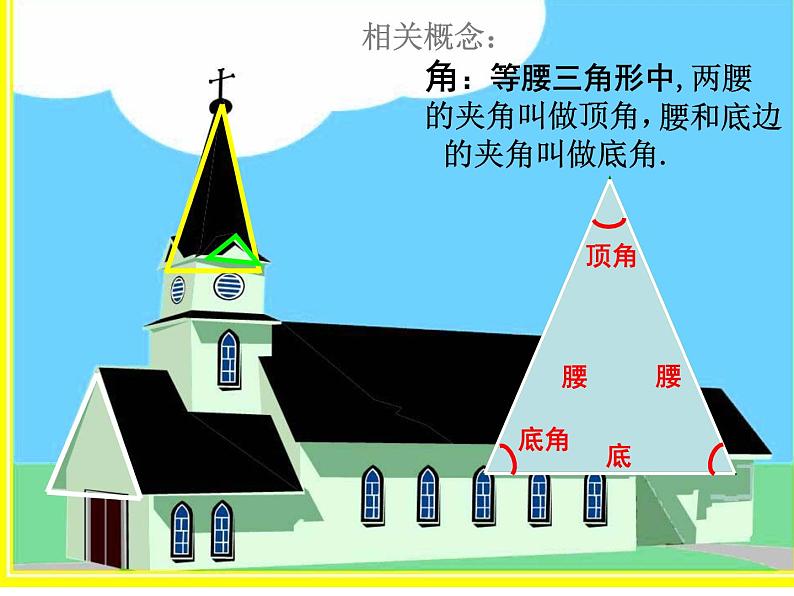
向同学们出示精美的建筑物图片　　　　　
角：等腰三角形中,两腰的夹角叫做顶角，
　　　　　　　腰和底边的夹角叫做底角.
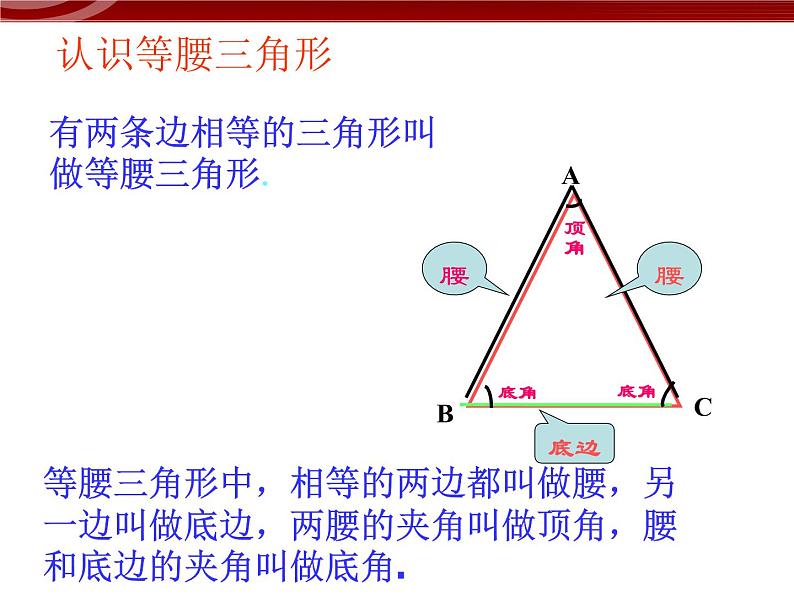
有两条边相等的三角形叫做等腰三角形.
等腰三角形中，相等的两边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角.
讨论：除了剪纸的方法,还可以怎样作(画)出一个等腰三角形?在你作(画)出的等腰三角形中,指明它的腰,底边,顶角的底角。
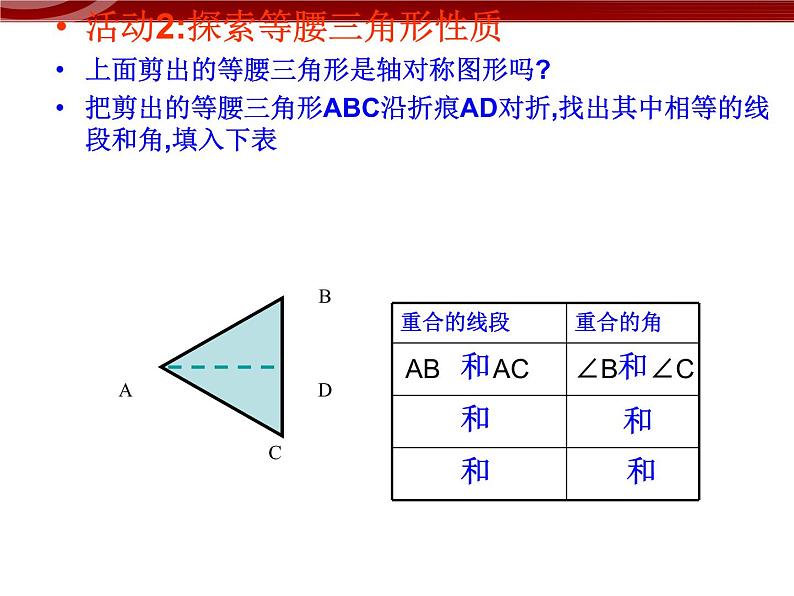
活动2:探索等腰三角形性质上面剪出的等腰三角形是轴对称图形吗?把剪出的等腰三角形ABC沿折痕AD对折,找出其中相等的线段和角,填入下表
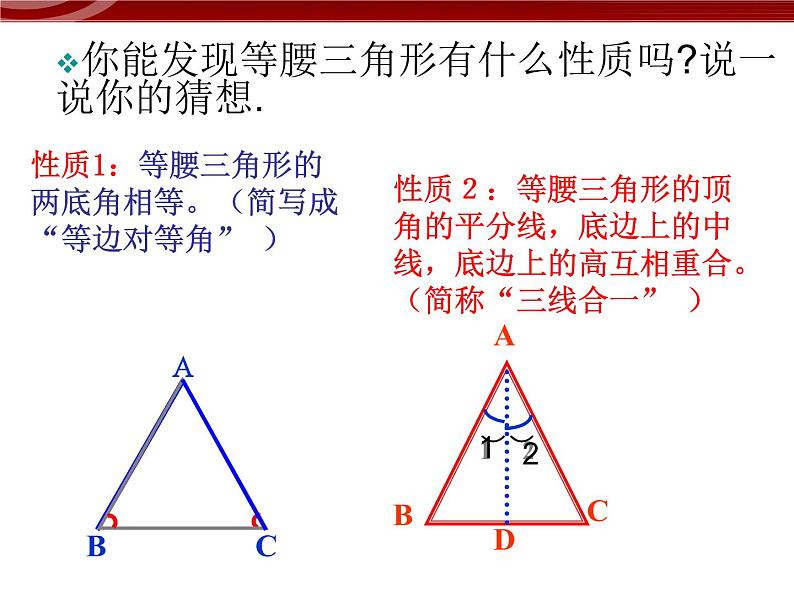
你能发现等腰三角形有什么性质吗?说一说你的猜想.
性质1：等腰三角形的两底角相等。（简写成“等边对等角” ）
性质２：等腰三角形的顶角的平分线，底边上的中线，底边上的高互相重合。（简称“三线合一” ）
性质2:等腰三角形的顶角的平分线，底边上的中线，底边上的高互相重合在△ABC中，AB =AC, 点 D在BC上1、∵AD ⊥ BC∴∠ = ∠ ，____= 。 2、∵AD是中线，∴ ⊥ ，∠ =∠ 。3、∵AD是角平分线，∴ ⊥ ， = 。
等腰三角形是轴对称图形.对称轴是底边上的中线(顶角平分线,底边上的高)所在直线
性质1:等腰三角形的两底角相在△ABC中， ∵ AC=AB（ ）∴ ∠B=∠C （ ）
证明性质1:等腰三角形的两个底角相等 (等边对等角) 。
已知：△ABC中，AB=AC
分析：1.如何证明两个角相等？
　　2.如何构造两个全等的三角形？
证明:在△ABC中,AB=AC,作底边BC的中线AD, 在 △ BAD 与△ CAD 中∵ AB=___ BD=___ AD=___ ∴ △ BAD ≌△ CAD( ) ∠B= ___
提问:这性质的条件和结论是什么?用数学符号如何表达条件和结论?
活动3:等腰三角形性质定理的证明
方法1:已知：△ABC中，AB=AC,AD是△ABC 的中线
证明性质２：等腰三角形的顶角的平分线，底边上的中线，底边上的高互相重合。（简称“三线合一” ）
求证：AD是△ABC的高和角平分线
证明: ∵,AD是△ABC的中线∴BD=CD在△ BAD ≌△ CAD中∵ AB=AC BD=CD AD= AD∴ △ BAD ≌△ CAD( SSS ) ∠BAD= CAD; ∠BDA= CDA∴AD是△ABC是角平分线又∵ ∠BDA+ CDA=1800∴ ∠BDA=CDA=900∴ AD是△ABC的高.
例1.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ ABC各角的度数
解:AB=AC,BD=BC=AD,∠ ABC= ∠ C= ∠ BDC∠ A= ∠ ADD(等边对等角)设A=x,则∠ BDC= ∠ A+ ∠ ABD=2x从而∠ ABC= ∠ C= ∠ BDC=2x于是在△ ABC中,有∠ A+ ∠ ABC+ ∠ C=x+2x+2x=1800.解得x=360在△ ABC中, ∠ A=360 ∠,ABC= ∠ C=720
活动4:等腰三角形性质定理的运用
练习1:小试牛刀 如图（1）在等腰△ABC中，AB =AC, ∠A = 36°,则∠B =——∠C=—
变式练习：1、如图（2）在等△ABC腰中，∠A = 50°, 则∠B =——，∠C=——2、如图（3）在等△ABC腰中，∠A = 120°则∠B =——，∠C=——
练习2： △ ABC是等腰直角三角形（AB=AC， ∠ BAC=90°），AD是底边BC上的高，标出∠ B， ∠ C， ∠ BAD， ∠ DAC的度数，图中有哪些相等的线段？
练习3：在△ ABC中，AB=AD=DC， ∠BAD=26°，求∠ B和∠ C的度数
1、求有关等腰三角形的问题，作顶角平分线、底边中线，底边的高是常用的辅助线；
2、熟练掌握求解等腰三角形的顶角、底角的度数；
3、掌握等腰三角形三线合一的应用。
这节课我们学习了什么?