数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.3 弧、弦、圆心角教课内容ppt课件

这是一份数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.3 弧、弦、圆心角教课内容ppt课件，共51页。PPT课件主要包含了尺规作图找圆心，知识回顾，回顾旧知，弦心距，圆的对称性，∠AOB为圆心角，圆心角，圆心角定理，学习任务，实验探究等内容，欢迎下载使用。

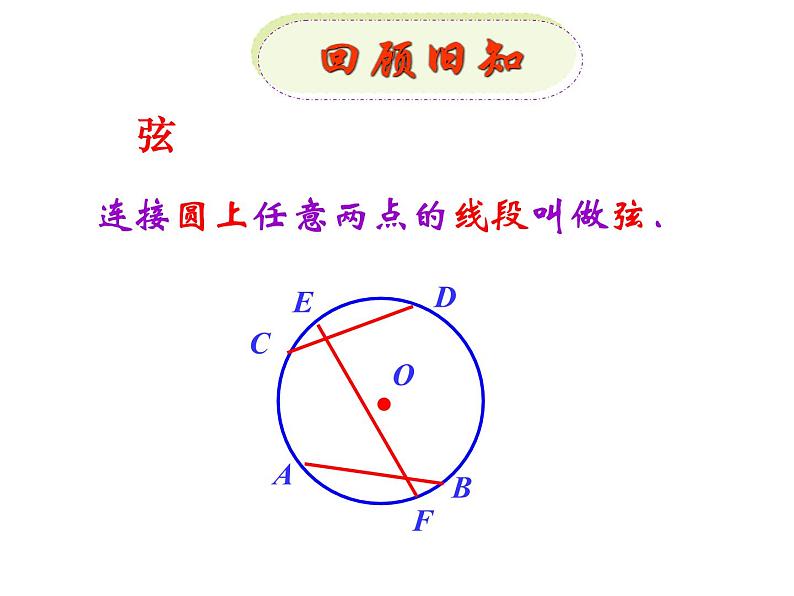
连接圆上任意两点的线段叫做弦．
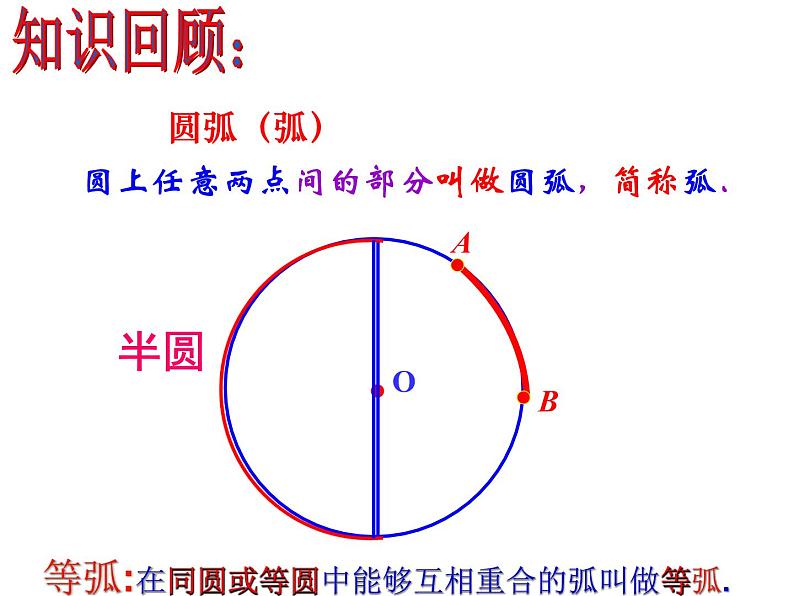
圆上任意两点间的部分叫做圆弧，简称弧．
等弧:在同圆或等圆中能够互相重合的弧叫做等弧.
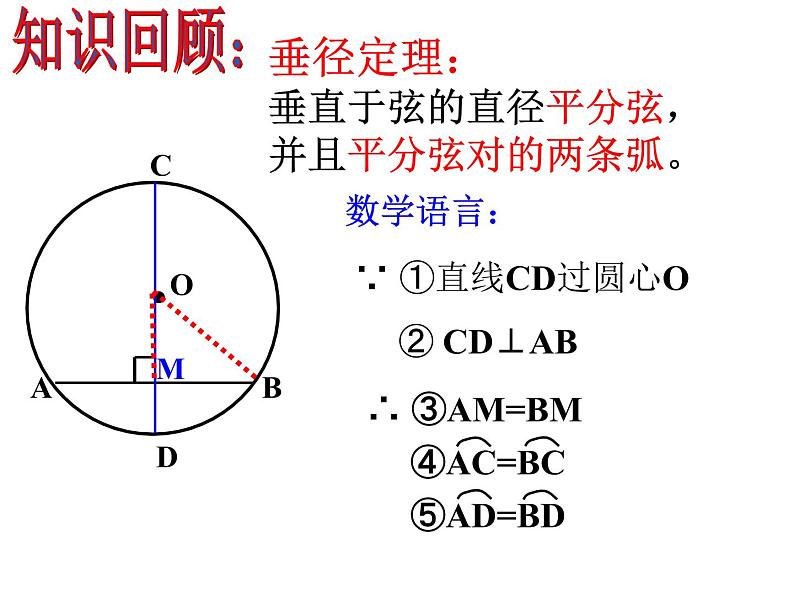
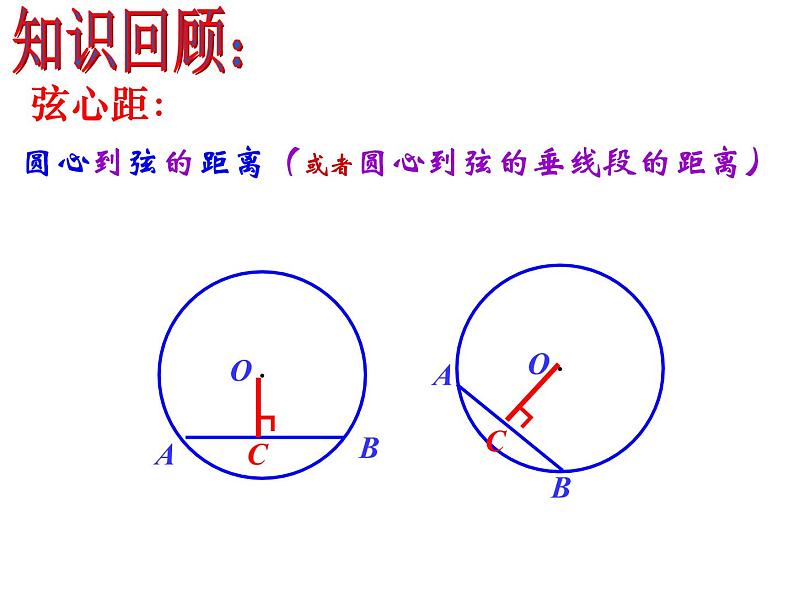
圆心到弦的距离（或者圆心到弦的垂线段的距离）
___________
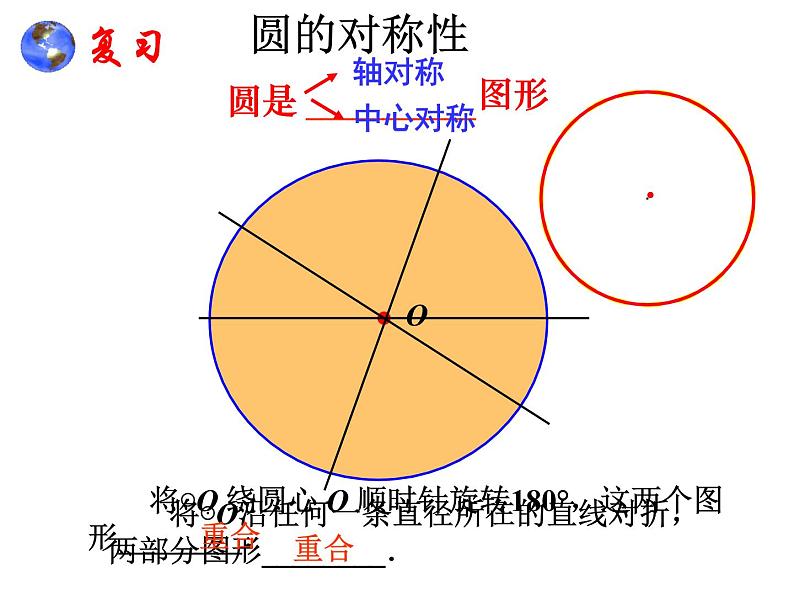
将⊙O沿任何一条直径所在的直线对折，两部分图形________．
将⊙O 绕圆心 O 顺时针旋转180°，这两个图形________．
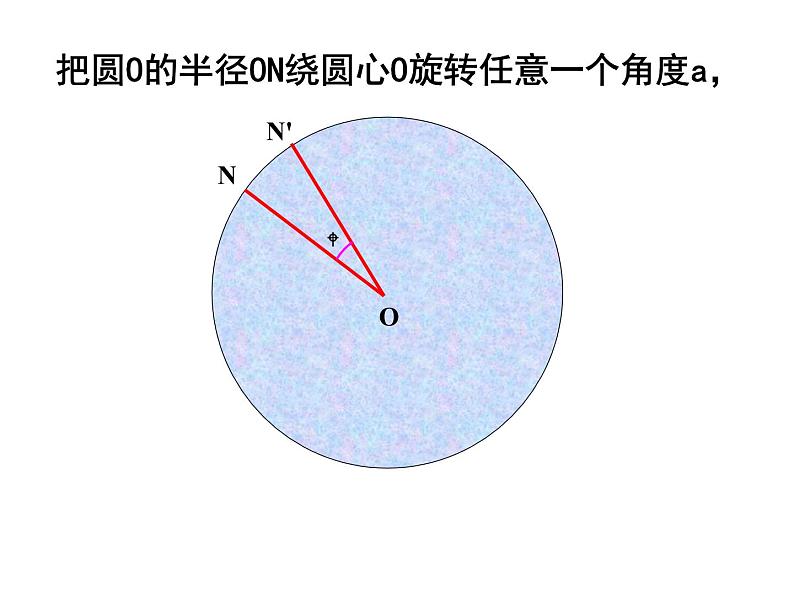
把圆O的半径ON绕圆心O旋转任意一个角度a，
定理：把圆绕圆心旋转任意一个角度后，仍与原来的圆重合,所以圆具有旋转不变性
由此可以看出，点N'仍落在圆上。
圆心角：把顶点在圆心的角叫做圆心角.
判别下列各图中的角是不是圆心角，并说明理由。
任意给圆心角，对应出现三个量：
想一想：这三个量之间会有什么关系呢？
下面我们一起来观察一下：在⊙O中有哪些圆心角？（并说出圆心角所对的弧，弦。）
圆心角： ∠AOB=∠ COD
下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系？
如果： ∠AOB=∠ COD
在⊙O中，分别作相等的圆心角∠AOB和∠A′OB′，将∠AOB旋转一定角度，使OA和O′A′重合．
你能发现哪些等量关系?
∵ ∠AOB=∠A1OB1
证明:∵OA=OC ，OB=OD， ∠AOB=∠COD, ∴ 当点A与点C重合时， 点B与点D也重合。 ∴　AB=CD，
圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。　　　　　　　　　　　　　
已知:如图∠AOB=∠ COD,求证: AB=CD，
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等.
1.圆的旋转不变性1.认识圆心角的定义； 2.理解并掌握圆心角定理；3.体会转化思想在圆心角定理中的应用；4.了解弧的度数4.体验分类讨论的思想（在圆的计算中，如果题中没有给出图形，但满足条件的图形又有多种情况，此时，解题要进行分类讨论。）
根据旋转的性质，∠AOB＝∠A′OB′，射线 OA与OA′重合，OB与OB′重合． 而同圆的半径相等，OA=OA′，OB=OB′， ∴点 A与 A′重合，B与B′重合．
再根据△AOB≌△A′O′B′，
在同圆或等圆中,相等的圆心角所对的弦的弦心距相等吗？.
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等．
①∠AOB=∠A′O′B′
弧、弦、圆心角、弦心距的关系定理
这四组关系分别轮换，其它关系是否成立?
弧、弦、圆心角关系定理的推论
在同圆或等圆中，相等的弧所对的圆心角相等，所对的弦相等，所对的弦的弦心距相等．
在同圆或等圆中，相等的弦所对的圆心角相等，所对的弧相等，所对的弦的弦心距相等．
在同圆或等圆中，相等的弦心距所对的圆心角相等，所对的弧相等，所对的弦相等．
在同圆或等圆中，有一组关系相等，那么所对应的其它各组关系均分别相等．
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，
同圆或等圆中，两个圆心角、圆心角所对的两条弧、圆心角所对的两条弦中如果有一组量相等，它们所对应的其余各组量也相等。
下面的说法正确吗?为什么?如图,因为
根据圆心角、弧、弦的关系定理可知：
不正确,因为不在同圆或等圆中.
∵把圆心角等分成360份,则每一份的圆心角是1º.同时整个圆也被分成了360份.
则每一份这样的弧叫做1º的弧.
这样,1º的圆心角对着1º的弧, 1º的弧对着1º的圆心角. n º的圆心角对着nº的弧, n º的弧对着nº的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
1相等的圆心角所对的弧相等。（ ）
2.如图，⊙O中，AB=CD, ，则
45号：试一试你的能力
1.如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么___________，_________________．（2）如果 = ，那么____________，______________．（3）如果∠AOB=∠COD，那么_____________，____________．（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？
相 等
因为AB=CD ，所以∠AOB=∠COD.
又因为AO=CO，BO=DO，
所以△AOB ≌ △COD.
又因为OE 、OF是AB与CD对应边上的高，
所以 OE = OF.
圆心到弦的距离叫做这条弦的弦心距.在同圆或等圆中,相等的圆心角所对的弦的弦心距相等.
如图： ⊙Ｏ的直径AB垂直于弦CD,AB与CD相交于点E，∠ COD＝1000，求BC,AD的度数
解:∵OC=OD,OE⊥CD
已知：如图，在⊙Ｏ中，弦ＡＢ＝ＣＤ．求证：ＡＤ＝ＢＣ　
例2如图,AB是⊙O的直径， ,∠COD=35°,求∠AOE的度数．
6、如图所示，已知以平行四边形ABCD的顶点A为圆心，以AB长为半径作圆交AD于点F，交BC于点G，BA的延长线交⊙A于点E。求证：弧EF=弧FG
如图,已知点O是∠EPF 的平分线上一点,P点在圆外，以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D.求证：AB=CD
分析:联想到角平分线的性质,作弦心距OM、ON，
要证AB=CD ，只需证OM=ON
⊙O1和⊙O2是等圆,AD‖O1O2,正确的是(　　)A.AB= CD且AB≠CD B.AB= CD且AB≠CDC.AB= CD且AB= CD D.以上都不对