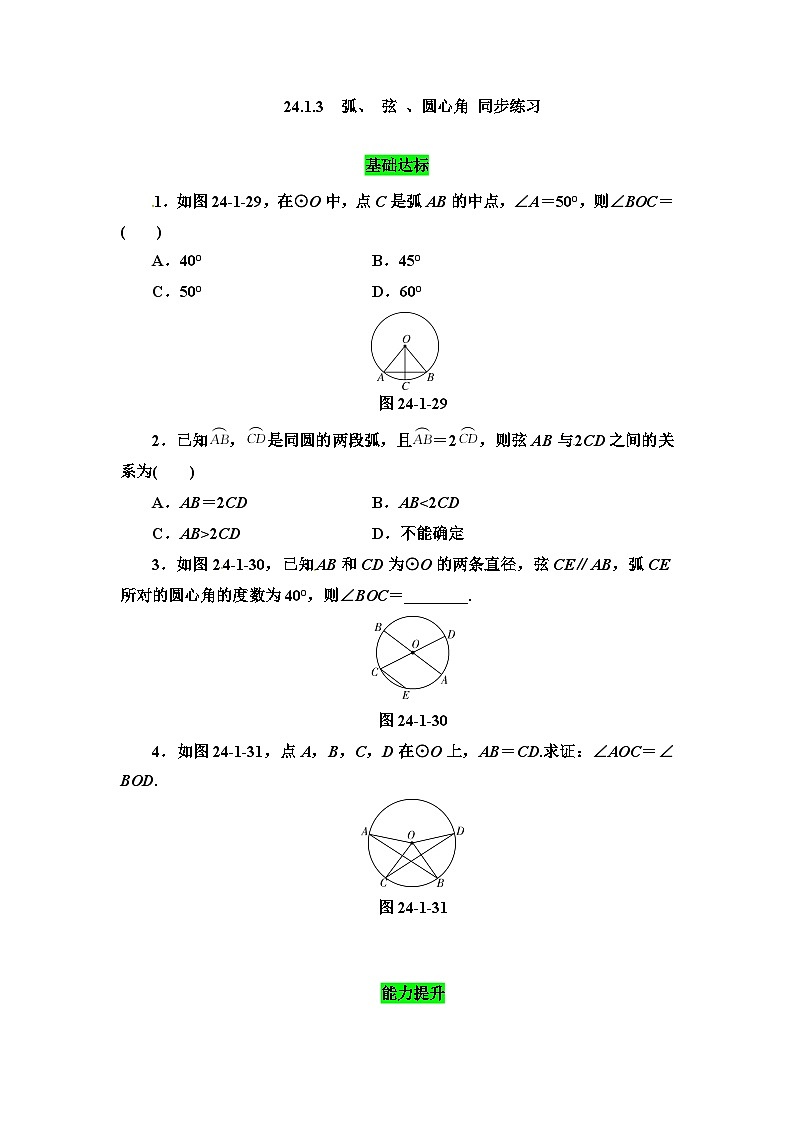
数学九年级上册24.1.3 弧、弦、圆心角教学课件ppt

课题

24.1.3　弧、弦、圆心角

授课人

素养目标

1.理解圆心角的概念和圆的旋转不变性，会辨析圆心角．

2．掌握在同圆或等圆中，圆心角与其所对的弦、弧之间的关系，并能应用此关系进行相关的证明和计算.

3．会用圆心角、弦、弧之间的关系解决有关问题，获得在圆中论证弧相等、角相等、线段相等的基本经验和方法.

教学重点

圆心角、弦、弧之间的关系及其理解应用.

教学难点

从圆的旋转不变性出发，发现并论证圆心角、弦、弧之间的关系.

授课类型

新授课

课时

教学步骤

师生活动

设计意图

复习回顾

问题：

1．圆是轴对称图形吗？圆的对称轴是什么？

2．由圆的轴对称性得到了圆中重要的垂径定理，垂径定理的内容是什么？请画出基本图形．

师生活动：学生完成复习任务，积极回答，教师及时鼓励、评价.

通过圆的轴对称性，对比学习圆的旋转不变性，从整体上更清晰地认识圆.

活动一：创设情境、导入新课

【课堂引入】

1．出示大小相等的两张矩形卡片，在卡片中心画好等圆．

出示问题：你看到了几个矩形，几个圆？

(将两张卡片重合，绕着中心任意旋转一个角度)

2．在图①中，你看到了几个矩形？几个圆？

归纳：将一个图形绕着某一点旋转任意角度，旋转前后的图形能够完全重合．

3．在图②中，矩形旋转了多少度？看到了几个矩形？说明了什么问题？看到了几个圆？说明了什么问题？

　　　　　　　　　①　　　　　　　　　　②

师生活动：教师进行演示，学生观察、讨论，针对问题进行回答，同时归纳圆和矩形的性质.

圆的旋转不变性是难点，通过动手操作旋转圆和矩形，让学生从直观上体会圆的旋转不变性及中心对称性.

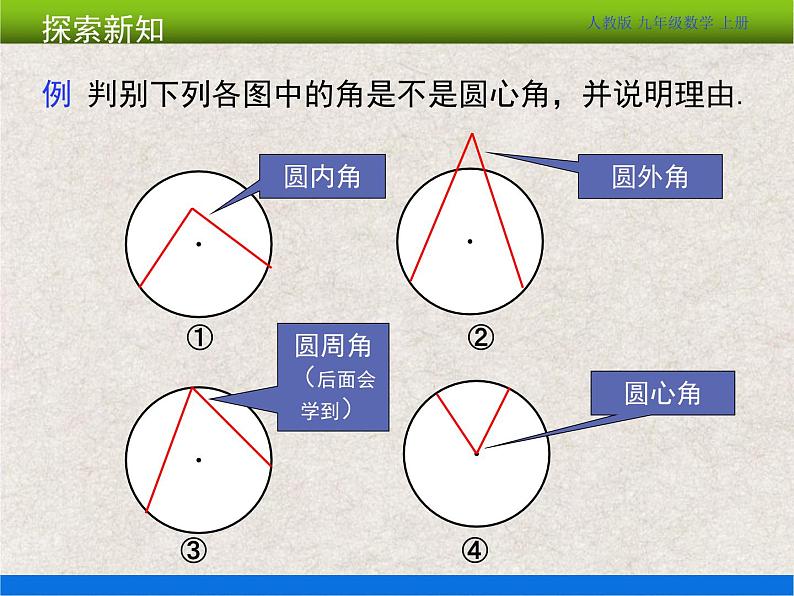
活动二：实践探究、交流新知

活动一：圆心角的概念

教师给出圆心角的概念，学生从图形中找出圆心角．

出示问题：

1．观察下图，∠AOB所对的弧是哪条？所对的弦是哪条？

2．计算：(1)在⊙O中，OA＝6，∠AOB＝60°，则AB＝6．

(2)在⊙O中，OA＝6，∠AOB＝90°，则AB＝6．

通过这两个题的计算你有什么发现？引导学生发现圆心角和它所对的弦有一定的关系．

活动二：观察分析、总结定理

教师提出问题1：在同圆或等圆中，相等的两个圆心角所对的弧相等吗？所对的弦相等吗？

如图，∠AOB＝∠A′OB′，那么AB与A′B′相等吗？为什么？与呢？

教师演示教具，引导学生发现：

把∠AOB连同绕圆心O旋转使OA与OA′重合，则当∠AOB＝∠A′OB′时，弦AB与A′B′重合，与重合，即AB＝A′B′，＝.

教师引导学生用语言总结结论．

教师提出问题2：若问题1中，缺少“在同圆或等圆中”这一条件，结论还能够成立吗？

学生交流、讨论，教师出示下图，学生分析图形得到结论．

教师提出问题3：若在同圆或等圆中，当两条弦相等时，则它们所对的圆心角或弧相等吗？

教师指导学生分析问题，得到圆心角、弧、弦之间的关系．

圆心角、弧、弦的关系：同圆或等圆中，两个圆心角、两条弧、两条弦中如果有一组量相等，那么它们所对应的其余各组量也相等．简单地说：知一得二．

即时小练：如图，AB是⊙O的直径，如果∠COA＝∠DOB＝60°，那么与线段OA相等的线段有OC，OD，OB，AC，CD，DB，与相等的弧有和.

让学生通过观察、猜想、证明、归纳得到新知识，培养学生分析问题、解决问题的能力.

活动三：开放训练、体现应用

1.培养学生正确应用所学知识的能力，增强应用意识．

2．变式训练补充了例题中没有涉及到的知识点，加强学生对知识的掌握和理解.

活动四：课堂检测

课堂检测是为了加深对所学知识的理解运用，在问题的选择上以基础为主，灵活运用所学知识解决问题，巩固新知.

课堂小结

1.课堂小结：

(1)你在本节课的学习中有哪些收获？有哪些进步？

(2)学习本节课后，还存在哪些困惑？

教师强调：运用定理时，不能忽略“在同圆和等圆中”这一重要条件．

2．布置作业：

教材第89页习题24.1第3，4题.

1.巩固、梳理所学知识，对学生进行鼓励，并进行思想教育．

2．因材施教，让不同程度的学生得到不同的发展.

板书设计

24.1.3　弧、弦、圆心角

1．圆心角：顶点在圆心的角．

2．在同圆或等圆中，两个圆心角、两条弧、两条弦中如果有一组量相等，则它们所对应的其余各组量也都分别相等．

在⊙O中，若①AOB＝A′OB′(圆心角相等)；

②＝(弧相等)；

③AB＝A′B′(弦相等)．

则

提纲挈领，重点突出.

教学反思

1.本节课学生通过观察、比较、操作、推理、归纳等活动，得出了圆的中心对称性、圆心角定理及推论，可以发展学生勇于探索的良好习惯，培养动手解决问题的能力.

2.本节课中，教师应让学生掌握解题方法，即要证弦相等或弧相等或圆心角相等，可先证其中一组量对应相等.掌握这个解题方法有助于提升学生的抽象思维能力.

反思，更进一步提升.