人教版九年级上册24.1.3 弧、弦、圆心角教课内容课件ppt

这是一份人教版九年级上册24.1.3 弧、弦、圆心角教课内容课件ppt，共26页。PPT课件主要包含了③ABCD，∴ADBC等内容，欢迎下载使用。

熊宝宝要过生日了！要把蛋糕平均分成四块，你会分吗？
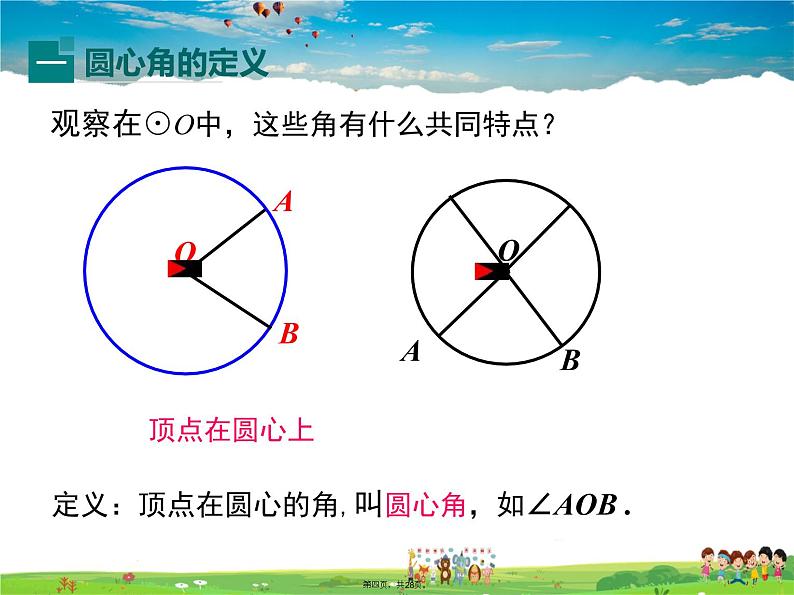
观察在⊙O中，这些角有什么共同特点？
定义：顶点在圆心的角,叫圆心角，如∠AOB .
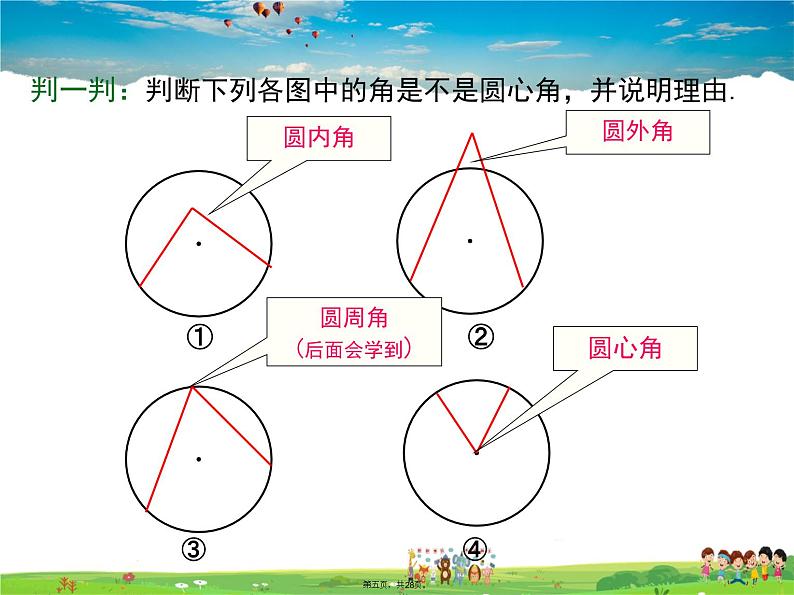
判一判：判断下列各图中的角是不是圆心角，并说明理由.
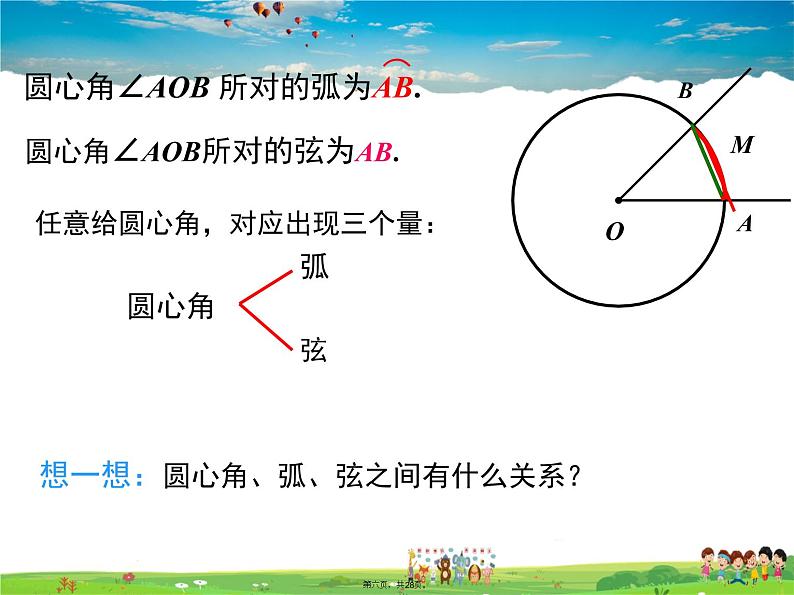
圆心角∠AOB所对的弦为AB.
任意给圆心角，对应出现三个量：
想一想：圆心角、弧、弦之间有什么关系？
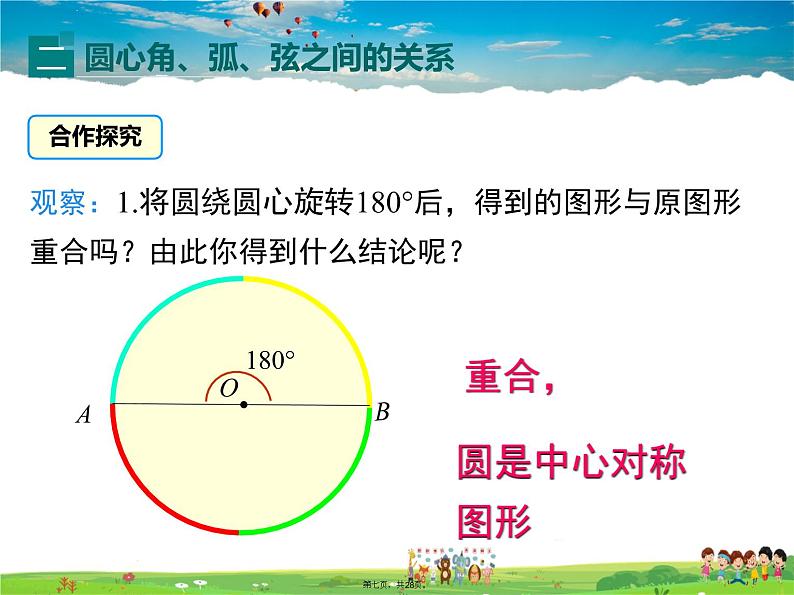
重合，圆是中心对称图形
观察：1.将圆绕圆心旋转180°后，得到的图形与原图形重合吗？由此你得到什么结论呢？
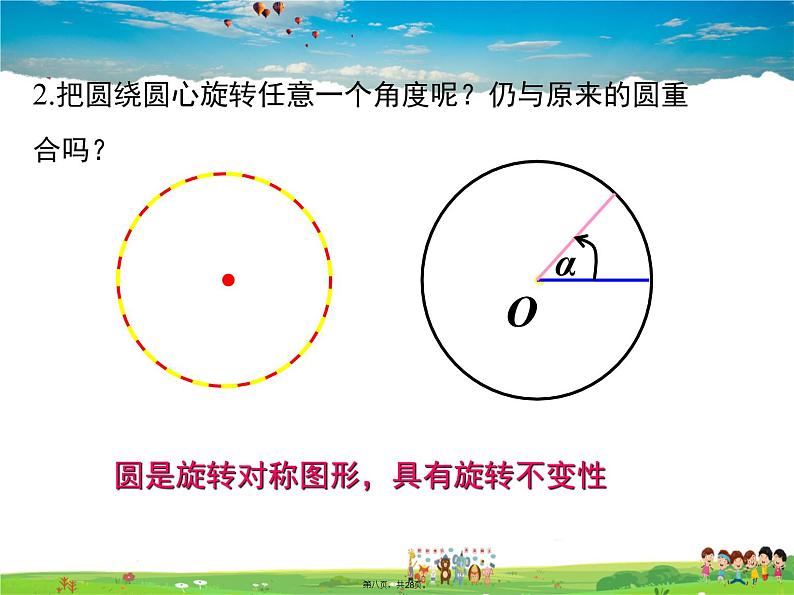
2.把圆绕圆心旋转任意一个角度呢？仍与原来的圆重合吗？
圆是旋转对称图形，具有旋转不变性
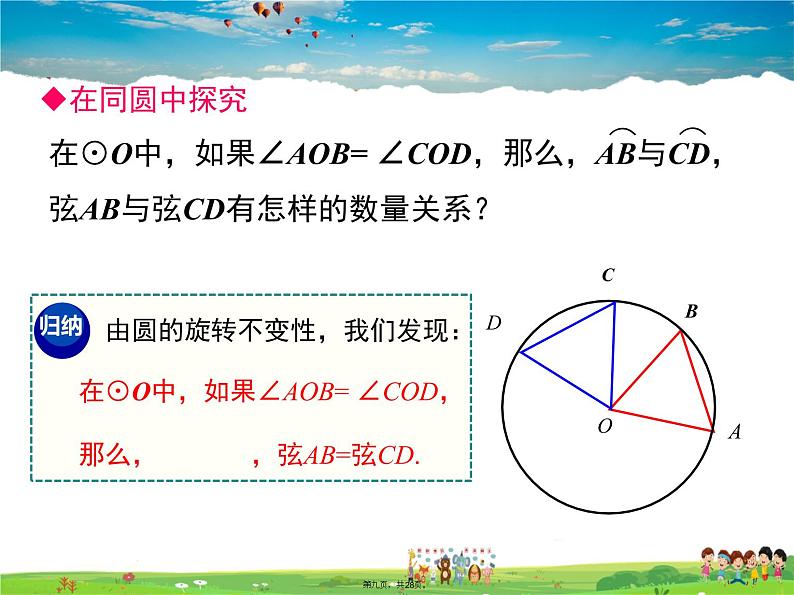
如图，在等圆中，如果∠AOB＝∠CO′D，你发现的等量关系是否依然成立？
在同圆或等圆中，如果圆心角相等，那么它们所对的弧相等，所对的弦相等．
弧、弦与圆心角的关系定理
在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等．
弧、弦与圆心角关系定理的推论
在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的优弧和劣弧分别相等．
温馨提示：一条弦对应两条弧，由弦相等得到弧相等时需要区分优弧和劣弧.
想一想：定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等”中，可否把条件“在同圆或等圆中”去掉？为什么？
1.等弦所对的弧相等. （ ）
2.等弧所对的弦相等. （ ）
3.圆心角相等，所对的弦相等. （ ）
∴ AB=AC.∴△ABC是等腰三角形．
∴△ABC是等边三角形，AB=BC=CA.
∴∠AOB＝∠BOC＝∠AOC.
例2 如图，在⊙O中，AB=AC ，∠ACB=60°.求证：∠AOB=∠BOC=∠AOC.
温馨提示：本题告诉我们，弧、圆心角、弦灵活转化是解题的关键．
变式1 如图，在⊙O中，AD=BC．求证：DC=AB．
变式2 如上图，在⊙O中，DC=AB．求证：AD=BC．
3.如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么_________，__________ __；（2）如果 ，那么_________， ；（3）如果∠AOB=∠COD，那么_________，_______；
第二十一页，共28页。
（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？
∵OE⊥AB，OF⊥CD，
∴Rt△AOE≌Rt△COF.
第二十二页，共28页。
4.已知：如图，A、B、C、D在⊙O上，AB=CD．求证：∠AOC=∠BOD．
∴∠AOB=∠COD.∴∠AOB-∠BOC=∠COD－∠BOC，即∠AOC=∠BOD．
证明：∵AB=CD（已知），
第二十三页，共28页。
证明：∵OB=OD，∴∠D=∠B.∵BD∥OC，∴∠D=∠COD，∠AOC=∠B.∴∠AOC=∠COD.
第二十四页，共28页。
第二十五页，共28页。
弦、弧、圆心角的关系定理
①要注意前提条件；②一条弦对应两条弧；③要灵活转化.
第二十六页，共28页。