初中数学人教版九年级上册24.1.3 弧、弦、圆心角课堂教学ppt课件

这是一份初中数学人教版九年级上册24.1.3 弧、弦、圆心角课堂教学ppt课件，共17页。PPT课件主要包含了圆的对称性，垂径定理及其推论，圆的中心对称性，一圆的中心对称性，圆具有旋转不变性，圆心角，圆心角所对的弧，在同圆或等圆中，ABCD，又∠ACB60°等内容，欢迎下载使用。

1.掌握圆心角的概念. 2.掌握在同圆或等圆中，圆心角、弦、弧中有一个量相等就可以推出其它的两个量对应相等，以及它们在解题中的应用.
圆的轴对称性（圆是轴对称 图形）
（1）若将圆以圆心为旋转中心，旋转180°，你能发现什么？
圆绕其圆心旋转180°后能与原来图形重合.因此 .
圆是中心对称图形，对称中心是圆心
圆绕圆心旋转任意角度α，都能够与原来的图形重合.____________________.
（2）若旋转角度不是180°，而是旋转任意角度，则旋转过后的图形能与原图形重合吗？
（1）相关概念 _______：顶点在圆心的角 ________________ ________________
圆心角所对的弦
(二) 圆心角、弧、弦、弦心距之间的关系
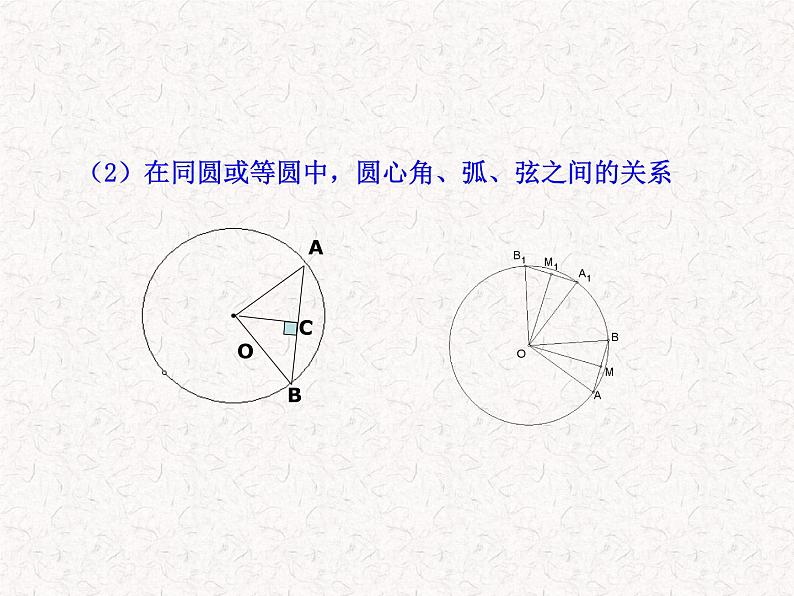
（2）在同圆或等圆中，圆心角、弧、弦之间的关系
__________，如果两个圆心角、两条弧、 两条弦或两条弦所对的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等.
【例1】如图，点O是∠EPF的平分线上的一点，以O为圆心的圆和角的两边分别交于点 A、B和C、D，求证：AB=CD.
证明：作OM⊥AB，ON⊥CD，M，N为垂足.
1、已知：如图，AB、CD是⊙O的两条弦，OE、OF为AB、CD的弦心距，根据本节定理及推论填空： （1）如果AB=CD，那么 ___________,________, _________. （2）如果OE=OF，那么 ___________,________,__________.
（3）如果AB=CD，那么 ______________,__________,____________. （4）如果∠AOB=∠COD，那么 _________,________,_________.
OE=OF AB=CD
∠AOB=∠COD OE=OF
证明：连结OA、OB，设分别与CD、EF交于点F、G ∵A为CD中点，B为EF中点 ∴OA⊥CD，OB⊥EF
故∠AFC=∠BGE=90° ①又由OA=OB，∴∠OAB=∠OBA ②且AM=BN ③∴△AFM≌△BGN ∴AF=BG∴OF=OG ∴DC=EF
证明:分别作O1C1⊥A1B1,O2C2 ⊥ A2B2,垂足分别为C1 、C2，∵A1B1∥O102，∴ O1C1= O2C2
如图：⊙ 和⊙ 是两个等圆，直线 平行于 . 分别交⊙ 于点 、 ，交⊙ 于点 、 .求证：
∴ AB=BC=CA.
∴ ∠AOB＝∠BOC＝∠AOC.
如图，在⊙O中， ,∠ACB=60°求证：∠AOB=∠BOC=∠AOC
2.如图，AB是⊙O 的直径， ∠COD=35°，求∠AOE 的度数．