北师大版（2024）3 乘法公式获奖教学课件ppt

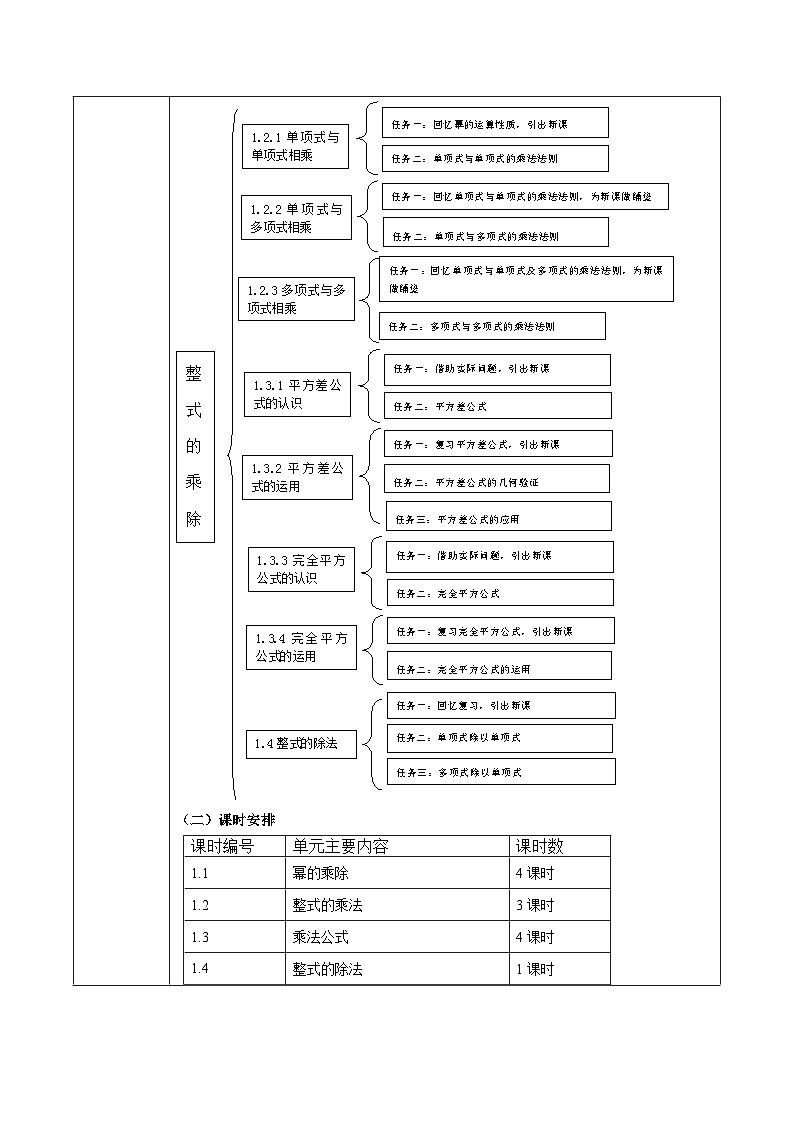
这是一份北师大版（2024）3 乘法公式获奖教学课件ppt，文件包含131平方差公式的认识pptx、131平方差公式的认识教案docx、第1章整式的乘除大单元教学设计doc等3份课件配套教学资源，其中PPT共25页， 欢迎下载使用。
小明和小兰分别负责两块区域的值日工作.小明负责一块边长为a米的正方形空地，小兰则负责一块长方形空地，长为正方形空地边长加5米，宽度是正方形空地边长减5米.有一天，小明对小兰说：“咱们换一下值日的区域吧，反正这两块地大小都一样.”你觉得小明说的对吗？为什么？
答：小明说的不对，长方形面积比正方形面积少了25平方米.
计算下列各式: (1) (x+2)(x-2);(2)(1+3a)(1-3a);(3) (x+5y)(x-5y);(4) (2y+z)(2y-z)。观察以上算式及其运算结果，你有什么发现?你能再举一些类似的例子吗?与同伴进行交流。
(1) (x+2)(x-2)=x2-2x+2x-4=x2-4;(2)(1+3a)(1-3a)=1-3a+3a-9a2=1-9a2;(3) (x+5y)(x-5y)=x2-5xy+5xy-25y2=x2-25y2;(4) (2y+z)(2y-z)=4y2-2yz+2yz-z2=4y2-z2。
上述各式的左边是二项式乘以二项式,即是两个数的和与它们的差的乘积，结果等于这两数的平方差.
例：(1)(3x－5)(3x＋5)=9x2+15x-15x-25=9x2-25 (2)(－2a－b)(b－2a)=-2ab+4a2-b2+2ab=4a2-b2
(a+b)(a-b)=a2-b2。两数和与这两数差的积，等于它们的平方差。
左边：a符号相同，b符号相反.
右边：符号相同项a的平方减去符号相反项b的平方.
公式变形:1.（a – b ) ( a + b) = a2 - b22.（b + a )( -b + a ) = a2 - b2
例1 利用平方差公式计算：(1) (5+6x)(5－6x)；(2) (x－2y)(x+2y)；(3) (－m+n)(－m－n) .
解：(1) (5+6x)(5－6x)= 52－(6x)2=25－36x2；(2) (x－2y)(x+2y)= x2－(2y)2= x2－4y2 ；(3) (－m+n)(－m－n) = (－m)2－n2 = m2－n2 .
如何计算(a-b)(-a-b)?你是怎样做的?
(a-b)(-a-b)=(a-b)[-（a+b）]=-(a-b)（a+b）=-（a2-b2）=-a2+b2
应用平方差公式计算时，应注意以下几个问题：(1)左边是两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数；(2)右边是相同项的平方减去相反项的平方；(3)公式中的a和b可以是具体数，也可以是单项式或多项式．
【知识技能类作业】必做题：
1.下列运算正确的是( 　　)A．(a＋b)(b－a)＝a2－b2B．(2m＋n)(2m－n)＝2m2－n2C．(xm＋3)(xm－3)＝x2m－9D．(x－1)(x＋1)＝(x－1)2
2.计算(2x+1)(2x–1)等于( 　　)A．4x2–1 B．2x2–1 C．4x–1 D．4x2+1
3.计算(1-a)(1+a)(1+a2)的结果是( )A. 1-a4 B. 1+a4 C.1- 2a2+a4 D.1+ 2a2+a4
4．利用平方差公式计算：(1)(a+3b)(a– 3b)；(2)(3+2a)(–3+2a)；(3)(–2x2–y)(–2x2+y).
解： (1) 原式=(a)2–(3b)2 =a2–9b2 ；(2) 原式=(2a+3)(2a–3)=(2a)2–32 =4a2–9；(3)原式=(–2x2 )2–y2 =4x4–y2.
【知识技能类作业】选做题：
5.为了应用平方差公式计算（a－b＋c）（a＋b－c），必须先适当变形.下列各变形中，正确的是（　D）A.[（a＋c）－b][（a－c）＋b] B.[（a－b）＋c][（a＋b）－c]C.[（b＋c）－a][（b－c）＋a] D.[a－（b－c）][a＋（b－c）]
6. 若(x+1)(x-1)(x2+1)(x4+1)=xn- 1,则n等于( )A.16 B.8 C.6 D.4
7.在化简整式（x－2）■（x＋2）＋▲中，“■”表示运算符号“－”“×”中的某一个，“▲”表示一个整式.（1）计算（x－2）－（x＋2）＋（－2＋y）；（2）若（x－2）（x＋2）＋▲＝3x2＋4，求出整式▲；（3）已知（x－2）■（x＋2）＋▲的计算结果是二次单项式，当▲是常数项时，直接写出■表示的符号及▲的值.
解：（1）原式＝x－2－x－2－2＋y＝y－6.（2）依题意得，▲＝3x2＋4－（x－2）（x＋2）＝3x2＋4－（x2－4）＝3x2＋4－x2＋4＝2x2＋8.（3）因为计算结果是二次式，所以■表示的运算符号是×.所以原式＝（x－2）（x＋2）＋▲＝x2－4＋▲.因为计算结果是单项式，所以▲的值为4.
平方差公式： (a+b)(a-b)=a2-b2。两数和与这两数差的积，等于它们的平方差。
结构特点：左边：a符号相同，b符号相反.右边：符号相同项a的平方减去符号相反项b的平方.
平方差公式： (a+b)(a-b)=a2-b2。两数和与这两数差的积，等于它们的平方差。
课题：1.3.1平方差公式的认识
1．下列各式能用平方差公式计算的是( ).A. (4a+b)(a-b) B. (-4a-b)(-4a+b)C. (4a+b)(-4a-b) D. (-4a+b)(4a-b)
2．计算下列各式，其结果是4y2－1的是（　A　）A.(－2y－1)(－2y＋1) B.(2y－1)2C.(4y－1)2 D.(2y＋1)(－2y＋1)
3.下列计算正确的是（　C　）A.（a＋3b）（a－3b）＝a2－3b2B.（－a＋3b）（a－3b）＝－a2－9b2C.（－a－3b）（a－3b）＝－a2＋9b2D.（－a－3b）（a＋3b）＝a2－9b2
4.若m2－n2＝4，那么（m－n）2（m＋n）2的值为（　C　）A.4 B.8 C.16 D.32
5．先化简，再求值：(x+1)(x-1)＋x2(1-x)+x3，其中x＝2.
解：原式=x2-1+x2-x3+x3=2x2-1.将x＝2代入上式，原式=2×22-1=7.