数学七年级下册（2024）2 整式的乘法优秀教学课件ppt

这是一份数学七年级下册（2024）2 整式的乘法优秀教学课件ppt，文件包含123多项式与多项式相乘pptx、123多项式与多项式相乘教案docx、第1章整式的乘除大单元教学设计doc等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。
单项式与单项式的乘法法则：单项式与单项式相乘，把它们的系数、相同字母的幂分别相乘，其余字母连同它的指数不变，作为积的因式。单项式与多项式的乘法法则：单项式与多项式相乘，就是根据分配律用单项式乘多项式的每一项，再把所得的积相加。
(1)如何计算(2a+b)(a+2b), (x+y)(x-1), (a2-b2)(a-b) ?你是怎么做的?
(2a+b)(a+2b)=2a·a+2a·2b+b·a+b·2b=2a2+4ab+ab+2b2=2a2+5ab+2b2(x+y)(x-1)=x·x+x·（-1）+y·x+y·（-1）=x2-x+xy-y (a2-b2)(a-b)=a2(a-b)-b2·(a-b)=a3-a2b-ab2+b3
任务：多项式与多项式的乘法法则
(2)一般地，如何进行多项式乘多项式的运算?与同伴进行交流。
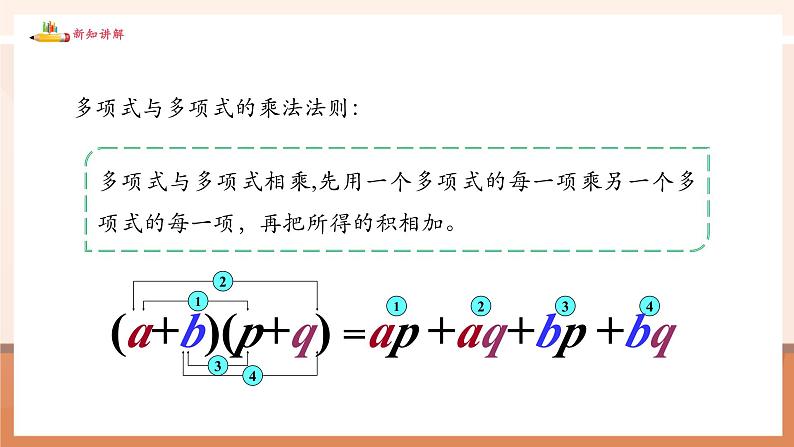
多项式乘多项式，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。
多项式与多项式的乘法法则：
例3 计算：(1) (1－x) (0.6－x)； (2) (2x + y) (x－y) .
解：(1)(1－x) (0.6－x)=1×0.6－1·x + x·0.6 + x·x =0.6－x－0.6x+ x2 =0.6－1.6x+ x2 (2)(2x + y) (x－y)=2x·x－2x·y + y·x－y·y =2x2－2xy+xy－y2 =2x2－xy－y2.
注意事项：(1)不要漏乘;(2)符号问题;(3)最后结果应化成最简形式.
(2)如图，一幅长为am、宽为bm的长方形风景画，画面的四周留有空白区域作装饰，其中四角均是边长为xm的正方形，正中间画面的面积是多少平方米?
正中间画面的面积=ab-2·x(a-2x)-2·x(b-2x)-4x2=ab-2xa+4x2-2xb+4x2-4x2=ab-2xa-2xb+4x2
多项式乘多项式谨记“循序追乘”：多项式乘多项式，先用第一个多项式的第一项乘第二个多项式的每一项，再用第一个多项式的第二项乘第二个多项式的每一项……依次类推．检验方法是若第一个多项式有x项，第二个多项式有y项，则去括号后合并同类项前应共有xy项．
【知识技能类作业】必做题：
1.计算(x-1)(x-2)的结果为（　　）A．x2+3x-2 B．x2-3x-2 C．x2+3x+2 D．x2-3x+2
2.已知M，N分别是2次多项式和3次多项式，则M×N( 　　)A．一定是5次多项式B．一定是6次多项式C．一定是不高于5次的多项式D．无法确定积的次数
3.已知ab=a+b+1，则（a﹣1）（b﹣1）=_______．
4．计算：(1)(x−3y)(x+7y)； (2)(2x + 5y)(3x−2y).
解： (1) (x−3y)(x+7y) =x2+7xy−3yx−21y2=x2+4xy–21y2； (2) (2x +5 y)(3x−2y)=2x•3x−2x• 2y+5 y• 3x−5y•2y=6x2−4xy+ 15xy−10y2=6x2 +11xy−10y2.
【知识技能类作业】选做题：
5.若多项式(x2＋mx＋n)(x2－3x＋4)展开后不含x3和x2项，则m，n的值分别是(　 　)A．3，5 B．5，3 C．4，2 D．2，4
6.用如图所示的A类、B类、C类卡片若干张，拼成一个长为2a＋3b，宽为a＋2b的长方形，则分别需要A类卡片 　 　⁠张，B类卡片 张，C类卡片 张.
7.在数学中，有些大数值问题可以通过用字母代替数转化成整式问题来解决.例如：试比较20192020×20192017与20192019×20192018的大小.解：设a＝20192019，x＝20192020×20192017，y＝20192019×20192018，则x＝（a＋1）（a－2），y＝a（a－1）.∵x－y＝ 　－2　⁠，∴x 　＜　⁠y（填“＞”“＜”或“＝”）.将上面的解题过程补充完整，并根据上述方法，试着计算下列各题：
（1）（m＋22.2022）（m＋14.2022）－（m＋18.2022）（m＋17.2022）；
解：（1）设x＝m＋18.2022.则原式＝（x＋4）（x－4）－x（x－1）＝x2－4x＋4x－16－x2＋x＝x－16＝m＋18.2022－16＝m＋2.2022.
多项式与多项式的乘法法则：多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加。
课题：1.2.3多项式与多项式相乘
1．计算(2x－3)(3x＋4)的结果是(　 　)A．－7x＋4 B．－7x－12C．6x2－12 D．6x2－x－12
2．下列多项式相乘结果为a2－3a－18的是(　 　)A．(a－2)(a＋9) B．(a＋2)(a－9)C．(a＋3)(a－6)　　 D．(a－3)(a＋6)
3.李老师做了个长方形教具，其中一边长为2a＋b，另一边长为a－b，则该长方形的面积为（　 ）A.6a＋b B.2a2－ab－b2C.3a D.10a－b
4.如果(x+a)(x+b)的结果中不含x的一次项，那么a、b满足(　 　)A．a=b B．a=0 C．a=–b D．b=0
5．若(x＋4)(x－6)＝x2＋ax＋b，求a2＋ab的值．
解：因为(x＋4)(x－6)＝x2－6x＋4x－24＝x2－2x－24，所以x2－2x－24＝x2＋ax＋b，因此a＝－2，b＝－24.所以a2＋ab＝(－2)2＋(－2)×(－24)＝4＋48＝52.
6.在一次测试中，甲、乙两同学计算同一道整式乘法：(2x＋a)(3x＋b)，甲由于抄错了第一个多项式中的符号，得到的结果为6x2＋11x－10；乙由于漏抄了第二个多项式中的系数，得到的结果为2x2－9x＋10.(1)试求出式子中a，b的值；(2)请你计算出这道整式乘法的正确结果．