数学七年级下册（2024）2 整式的乘法教学演示课件ppt

这是一份数学七年级下册（2024）2 整式的乘法教学演示课件ppt，共35页。PPT课件主要包含了垂钓区，品茗观赏区，池塘面积a·b，怎么计算呢，乘法分配律，单项式与多项式相乘，多项式与多项式相乘，基础题，m3＋m2，－3x3＋12x2等内容，欢迎下载使用。
1.理解并掌握单(多)项式与多项式相乘的运算法则.2.能够灵活地进行单(多)项式与多项式相乘的运算.
某茶园的农业项目经理想要规划和建设一个集茶叶种植、休闲旅游为一体的茶园生态农庄，故决定打算对茶园进行改造，以下是他的改造计划.
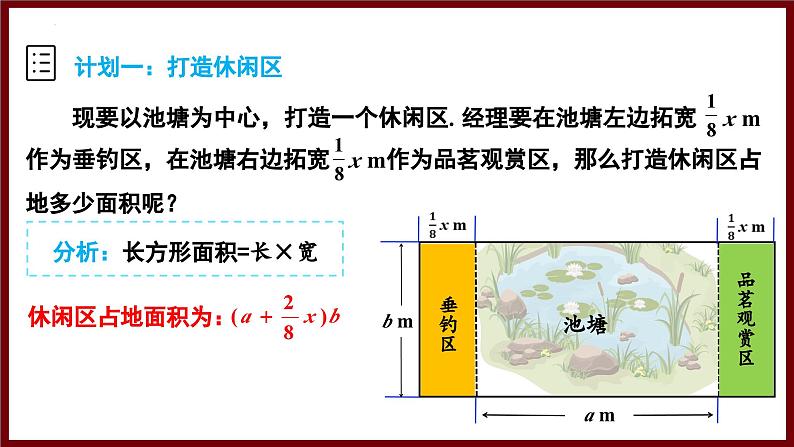
现要以池塘为中心，打造一个休闲区. 经理要在池塘左边拓宽 x m作为垂钓区，在池塘右边拓宽 x m作为品茗观赏区，那么打造休闲区占地多少面积呢？
分析：长方形面积=长×宽
可以用池塘面积加上两边扩建的面积
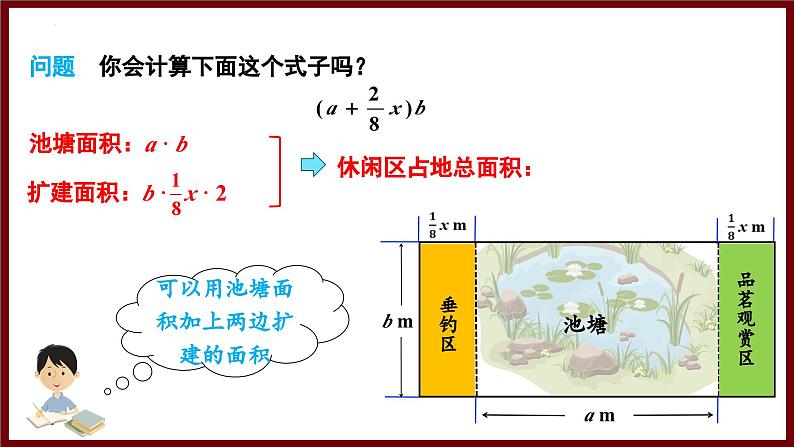
问题 你会计算下面这个式子吗？
思考 对比下面两个式子，你有什么发现？
分析：由于休闲区总面积一定， 所以可得到：
是根据乘法分配律计算的
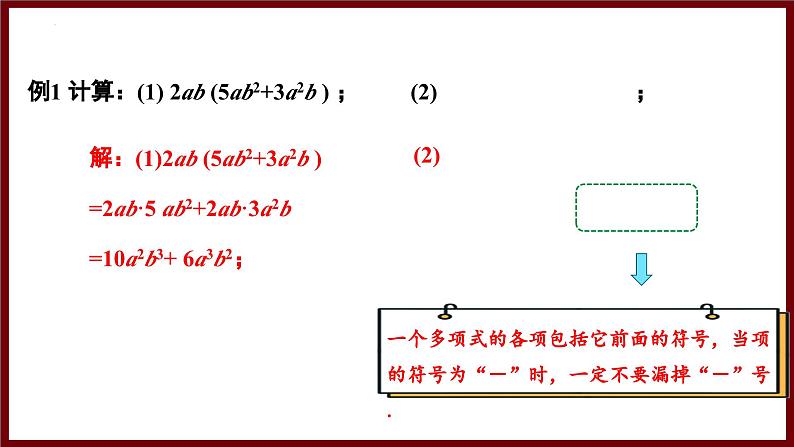
例1 计算：(1) 2ab (5ab2+3a2b ) ； (2) ；
解：(1)2ab (5ab2+3a2b ) =2ab·5 ab2+2ab·3a2b=10a2b3+ 6a3b2；
例1 计算： (3)5 m2n (2n+3m-n2 ) ； (4)2 ( x+y2z+xy2z3 )·xyz．
解：(3) 5 m2n (2n+3m-n2 ) =5m2n·2n+5m2n·3m +5m2n· ( -n2) =10m2n2+15m3n - 5m2n3；
(4)2 ( x+y2z+xy2z3 )·xyz = (2x +2y2z+2xy2z3) ·xyz =2x·xyz+2y2z·xyz+2xy2z3·xyz =2x2yz+2xy3z2+2x2y3z4 ．
如图所示，经理打算在茶园上边拓宽 f m，右边拓宽e m，使扩建后的长方形茶园长为(c+e)m，宽为( d+f )m，此时茶园的总面积为多少？
茶园总面积为：茶园的长×茶园的宽 =(c+e)( d+f )
可以尝试多用几种方法表示
茶园总面积还可以表示为： d (c+ e)+ f (c+ e) ； c (d+ f )+e (d + f ) ； cd + ed + cf + ef
思考 对比下面几个式子，你有什么发现？
(c+e)( d+f )
d (c+e) + f (c+e)
c( d + f )+e ( d+ f )
cd + ed + cf + ef
分析：由于扩建后茶园的总面积一定，所以可得到： (c+e)( d+f )=d (c+e) + f (c+e) =c( d + f )+e ( d+ f )=cd + ed + cf + ef
(c+e)( d+f )=d (c+e) + f (c+e) =c( d + f )+e ( d+ f )=cd + ed + cf + ef
例2 计算： (1)(1 - x)(0.6 - x)； (2) (2x + y)(x - y)；
解：(1)(1 - x)(0.6 - x) =1×0.6+ 1 · (-x) - x · 0.6 + x · x =0.6 - x - 0.6x + x2 =0.6 - 1.6x + x2；
(2) (2x + y)(x - y) =2x·x - 2x · y + y · x - y · y =2x2 - 2xy + xy- y2 =2x2 - xy - y2；
例2 计算： (3)(m - 2n)(m²+mn - 3n²)； (4) (3x² - 2x + 2)(2x + 1).
解:(3)(m - 2n)(m²+mn - 3n²) =m·m² +m·mn +m·(-3n²) +(-2n)·m²+(-2n)·mn +(- 2n)·(-3n²) =m3 + m²n - 3mn² - 2m²n - 2mn² + 6n3 =m3 - m²n - 5mn² + 6n3；
(4) (3x² - 2x+2)(2x+1) = 3x²·2x+ (- 2x)·2x+2×2x+3x²·1+ (- 2x)×1+2×1 = 6x3 - 4x²+4x+3x² - 2x+2 = 6x3 - x²+2x+2.
如图所示，扩建后的茶园长为g m，宽为h m，为了方便游客体验茶叶采摘，经理打算在扩建后的长方形茶园中修建两条宽度为x m的道路，每条道路的两边互相平行(每条道路与长方形茶园的宽平行)，此时剩余种茶面积为多少？
剩余种茶面积为：( g - 2x ) h = gh - 2hx (m2)
试营业后，有游客反映人流太大不方便采摘，为了增加出入口便于人员分流，经理决定新修一条宽为x m的小路平行于长方形茶园的长，那么此时剩余多少种茶面积呢？
剩余种茶面积为：( g - 2x ) ( h - x ) = gh - gx -2hx + 2x2 (m2)
字母表示：p(a＋b＋c)＝pa＋pb＋pc (p，a，b，c都是单项式)
多项式与多项式相乘: 先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.
字母表示：(a＋b)(p＋q)＝ap＋aq＋bp＋bq (a，b，p，q都是单项式)
1.(2024兰州)计算：2a(a-1)-2a2=( )A. a B. -a C. 2a D. -2a
2.今天数学课上，老师讲了单项式乘多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：-3xy(4y-2x-1) = -12xy2+6x2y＋□，□的地方被钢笔水弄污了，你认为□内应填写 (　　)A. 3xy B. -3xy C. -1 D. 1
3.下列多项式相乘结果为a2－3a－18的是(　　)A．(a－2)(a＋9) B．(a＋2)(a－9)C．(a＋3)(a－6)　　 D．(a－3)(a＋6)
(1)(-4x)·(2x2+3x-1)；
解：(1)(-4x)·(2x2+3x-1) = (-4x)·(2x2)+(-4x)·3x+(-4x)·(-1)
= -8x3-12x2+4x；
(2)
(3) -2x2·(xy+y2)-5x(x2y-xy2)；
(3) -2x2·(xy+y2)-5x(x2y-xy2)= (-2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x)·(-xy2)
= -2x3y+(-2x2y2)+(-5x3y)+5x2y2
= -7x3y+3x2y2；
(4) (x - 8y)(x - y).
(4) (x - 8y)(x - y)=x·x+x·(- y)+(- 8y)·x+(- 8y)·(- y)=x2 -xy-8xy＋8y2=x2 -9xy＋8y2.
5. 先化简，再求值：(a－2b)(a2＋2ab＋4b2)-a(a-5b)(a＋3b)，其中 a = -1，b = 1.
当 a = -1，b = 1时，
解：原式 = a·a2+a·(2ab)+a·(4b2)- 2b ·a2- 2b · 2ab- 2b · 4b2 -(a2-5ab)(a＋3b) = a3-8b3-(a2·a+a2·3b-5ab·a-5ab·3b)
= a3-8b3-a3-3a2b＋5a2b＋15ab2
= - 8b3＋2a2b＋15ab2.
原式 = -8× 13 ＋2 × (-1)2 ×1 +15 ×(-1) × 12 = -21.
单(多)项式与多项式相乘
根据分配律用单项式乘多项式的每一项，再把所得的积相加.
先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.
字母表示：p(a＋b＋c)＝pa＋pb＋pc
字母表示：(a＋b)(p＋q)＝ap＋aq＋bp＋bq
知识点1　单项式与多项式相乘
1. 计算x(x－1)的结果为(　B　)
2. (教材随堂练习第1题改编)计算：
(1)m2·(2m＋1)＝ ⁠；
(2)－3x(x2－4x)＝ ⁠.
3. 已知x2＋x＝3，则7＋x(x＋1)＝ ⁠.
(1)5·(m＋m2n)·mn3；
解：原式＝(5m＋5m2n)·mn3 ＝5m2n3＋5m3n4；
4. (教材例题改编)计算：
知识点2　多项式与多项式相乘5. 计算(x－1)(x＋5)的结果为(　D　)
6. (教材例题改编)填空：(1)(3x－1)(x＋2)＝ ⁠；(2)(a＋2b)(a－2b)＝ ⁠；(3)( ＋4)(x＋3)＝x2＋ x＋12.
7. (教材习题第2题改编)计算：(1)(－2x＋y)2；
解：原式＝(－2x＋y)(－2x＋y) ＝(－2x)·(－2x)＋(－2x)·y＋y·(－2x)＋y2 ＝4x2－4xy＋y2；
解：原式＝3x2＋24xy－xy－8y2 ＝3x2＋23xy－8y2.
8. (教材复习题第7题改编)先化简，再求值：m(m＋5)－(m－3)(m＋2)，其 中m＝－1.
解：原式＝m2＋5m－(m2－m－6) ＝m2＋5m－m2＋m＋6 ＝6m＋6.因为m＝－1，所以原式＝(－1)×6＋6＝0.
知识点3　单(多)项式乘多项式的实际应用
9. 随着机械化水平的提高，收割机成为收割小麦的主要工具，若收割机 每小时可以收割(6ab2)2平方米小麦，在不考虑收割机调头及卸粮时间的情 况下，则收割机(a2b＋2ab)小时后能收割小麦 平方米.
(36a4b5＋72a3b5)
10. 如图所示的大长方形区域为一片麦田，若计划将该麦田改造为高标准 良田，将原麦田的长缩短a，宽缩短b，则改造后的长方形高标准良田的面 积(阴影部分)为 ⁠.
ab－4a－6b＋24
11. 已知y＝3x＋2，则3x(y＋1)－y(1＋3x)＋4的值为(　B　)
12. 若5y－2x＝4，xy＝3，则代数式(5－2x)(1＋y)的值为(　C　)
13. 已知A＝2m2＋m－a，B＝－5m，C＝10m3＋5m2－3m＋4，若A·B＋C 的值与m无关，则a的值为(　B　)
14.北宋沈括在《梦溪笔谈》中创立了“隙积术”引出了数酒坛的问题：如图，酒馆店家将酒坛一层层堆放，从上往下第一层有4排，每排有3个酒坛，共有12个酒坛，往下每一层比上一层多一排，且每一排比上一层多一个酒坛，则第n层的酒坛共有 ⁠个酒坛.
15. 欢欢在计算A×(－4x)时，因抄错运算符号，将乘号错写为加号，得到 的结果是2x2＋3x－1，(1)求正确的计算结果B；
解：根据题意可得，A＝2x2＋3x－1－(－4x)＝2x2＋7x－1，则正确的计算结果B＝(2x2＋7x－1)×(－4x)＝－8x3－28x2＋4x；
(2)若C＝2x2＋6x，在(1)的条件下，计算(A－C)·B的结果.
解：(A－C)·B＝[(2x2＋7x－1)－(2x2＋6x)]·(－8x3－28x2＋4x)＝(x－1)(－8x3－28x2＋4x)＝x(－8x3－28x2＋4x)－(－8x3－28x2＋4x)＝－8x4－28x3＋4x2＋8x3＋28x2－4x＝－8x4－20x3＋32x2－4x.
16. (综合与实践·操作探究)运用代数思想也能巧妙地解决一些图形问题. 现有若干张如图所示的三种卡片(a＜b).
【操作发现】(1)请你用1张甲卡片，2张乙卡片，3张丙卡片拼成一个长方 形(不重叠，无缝隙)，画出一种拼法的示意图，并根据拼图前后图形面积 之间的关系写出一个等式；
解：用1张甲卡片，2张乙卡片，3张丙卡片拼成一个长方形如解图所示(拼法不唯一，合理即可)，由图形面积关系可以得到的等式为(a＋b)(a＋2b)＝a2＋2b2＋3ab；