北师大版（2024）七年级下册（2024）3 探究三角形全等的条件课前预习课件ppt

这是一份北师大版（2024）七年级下册（2024）3 探究三角形全等的条件课前预习课件ppt，共19页。PPT课件主要包含了边边边SSS，几何语言，角边角ASA，角角边AAS，①两边及夹角，②两边及其一边的对角，连接AC，①和④等内容，欢迎下载使用。
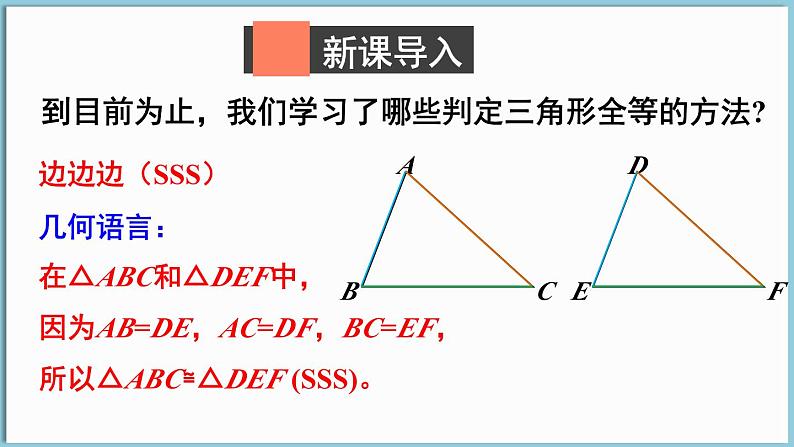
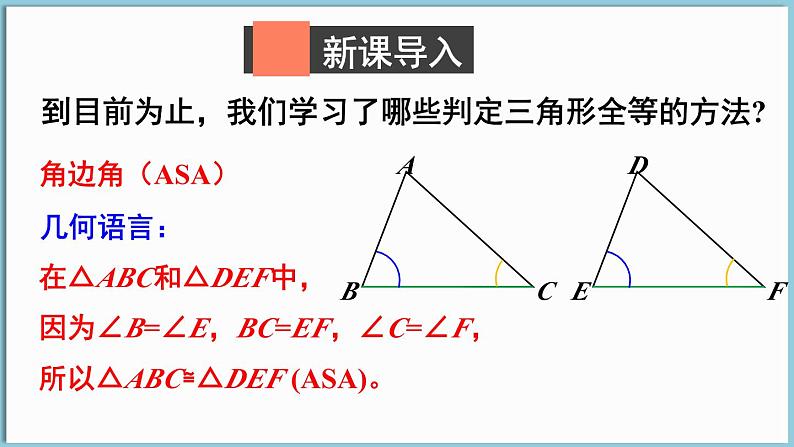
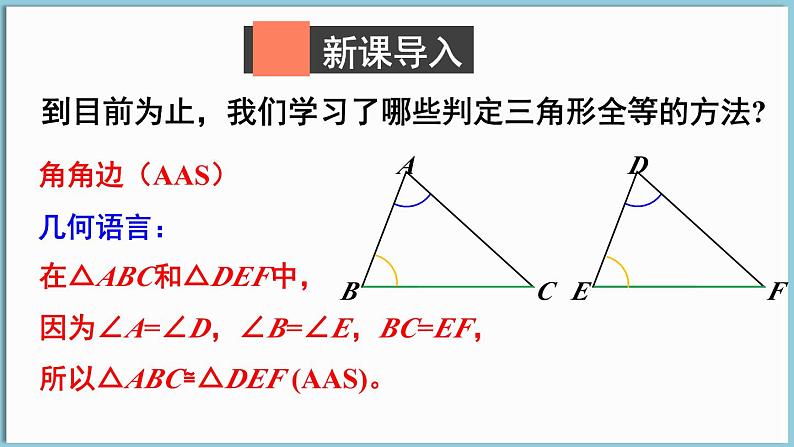
到目前为止，我们学习了哪些判定三角形全等的方法?
在△ABC和△DEF中，
所以△ABC≌△DEF (SSS)。
因为AB=DE，AC=DF，BC=EF，
所以△ABC≌△DEF (ASA)。
因为∠B=∠E，BC=EF，∠C=∠F，
所以△ABC≌△DEF (AAS)。
因为∠A=∠D，∠B=∠E，BC=EF，
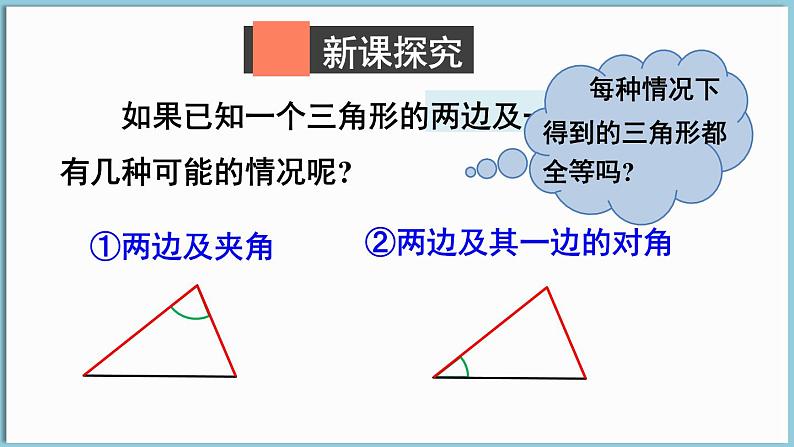
如果已知一个三角形的两边及一角，那么有几种可能的情况呢?
如果“两边及一角”条件中的角是两边的夹角，情况会怎样呢?
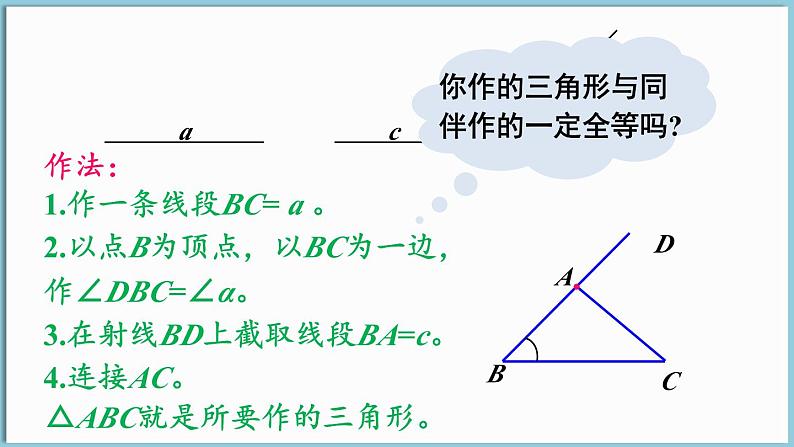
如图，已知线段a，c，∠α，用尺规作△ABC，使BC= a，AB=c，∠ABC=∠α。
1.作一条线段BC= a 。
2.以点B为顶点，以BC为一边，作∠DBC=∠α。
3.在射线BD上截取线段BA=c。
△ABC就是所要作的三角形。
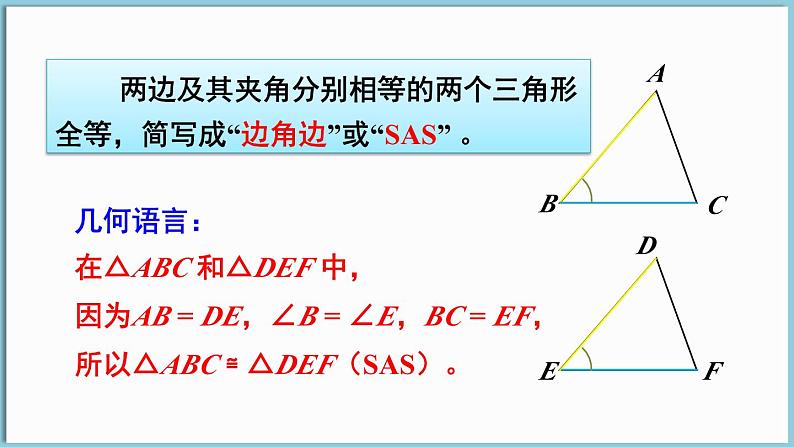
在△ABC 和△DEF 中，
因为AB = DE，∠B = ∠E，BC = EF，
所以△ABC ≌ △DEF（SAS）。
两边及其夹角分别相等的两个三角形全等，简写成“边角边”或“SAS” 。
1.分别找出各图中的全等三角形，并说明理由。
解：(1) △ABC≌△EFD (SAS) ； (2) △ABC≌△CDA (SAS) 。
【课本P104 随堂练习 第1题】
2.小明做了一只如图所示的风筝，其中∠EDH =∠FDH，ED = FD 。将上述条件标注在图中小明不用测量就知道EH = FH ，请你说明理由
解：在△DEH 和△DFH 中，
所以 △DEH ≌ △DFH（SAS）。
因为ED = FD，∠EDH = ∠FDH， DH = DH，
【课本P104 随堂练习 第2题】
所以 EH = FH 。
如果“两边及一角”条件中的角是其中一边的对角，情况会怎样呢?
如图，已知△ABC的AB边和边长为l的AC边，以及AC边的对角∠B，你能用尺规确定顶点C的位置吗?
发现:顶点 C 可能存在两个位置。
1.如图，在下列三角形中，哪两个三角形全等?
2.如图，CA 平分∠DCB，CB=CD ，DA的延长线交BC于点E，若∠EAC=49°，则∠BAC 的度数为________。
2.在△ABC 中，AB = AC，AD 是∠BAC的角平分线。 那么 BD 与 CD 相等吗?为什么?
解：相等 。理由：因为AD是∠BAC 的角平分线，所以∠BAD = ∠CAD。
所以△ABD ≌△ACD（SAS）。
所以 BD = CD。
又因为 AB=AC，AD =AD，
3.如图，BC∥EF，BC＝BE，AB＝FB，∠1＝∠2，若∠1＝60°，求∠C 的度数。
又因为在△ABC 和 △FBE 中，
BC = BE，AB = FB，
所以 △ABC ≌△FBE (SAS)，
所以∠C ＝∠BEF。
所以 ∠C ＝∠BEF ＝∠1 ＝ 60°。
解：因为∠1＝∠2，所以∠ABC ＝∠FBE 。
因为 BC ∥ EF，
4.如图，在湖泊的岸边有A、B两点，难以直接量出A、B两点间的距离。你能设计一种量出A、B 两点之间距离的方案吗?
因为CA = CD，∠ACB = ∠DCE，CB = CE，
解：在△ABC 和△DEC 中
所以△ABC ≌ △DEC（SAS）。
所以 AB = DE。