北师大版（2024）七年级下册（2024）3 探究三角形全等的条件教学演示ppt课件

这是一份北师大版（2024）七年级下册（2024）3 探究三角形全等的条件教学演示ppt课件，共35页。PPT课件主要包含了怎么办啊，为什么呢，玻璃1，玻璃2，所以ADAE，基础题，综合题，拓展提升等内容，欢迎下载使用。
1.探索并正确理解三角形全等的判定方法“ASA”和“AAS”.2.能运用三角形全等的判定方法“ASA”和“AAS”说明两个三角形全等.
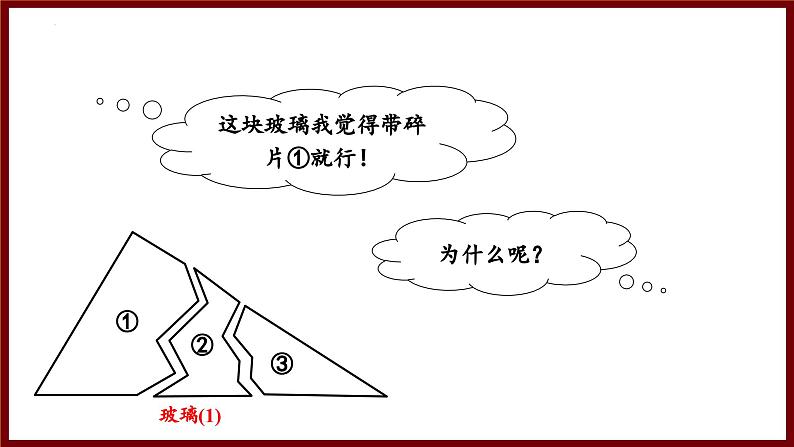
小钰在家中整理物品时，不小心将家里的几个三角形玻璃装饰品打碎了，她已经将碎片收集好并拼好，决定带最少的玻璃碎片去店里制作新的三角形玻璃装饰，带哪块去合适呢？
这块玻璃我觉得带碎片①就行！
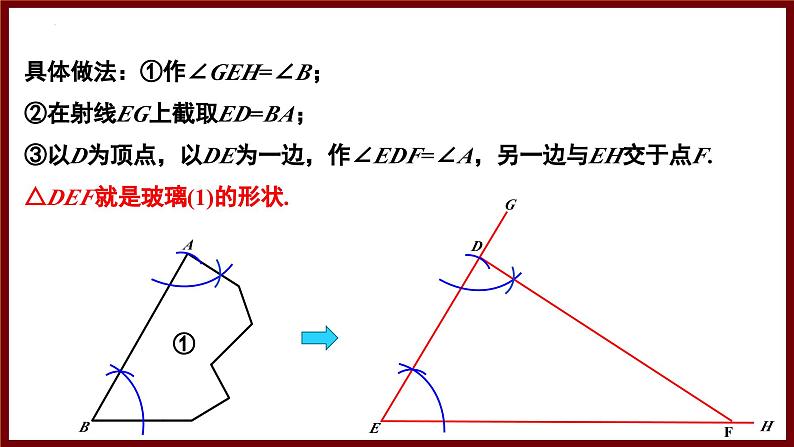
具体做法：①作∠GEH=∠B；②在射线EG上截取ED=BA；③以D为顶点，以DE为一边，作∠EDF=∠A，另一边与EH交于点F.△DEF就是玻璃(1)的形状.
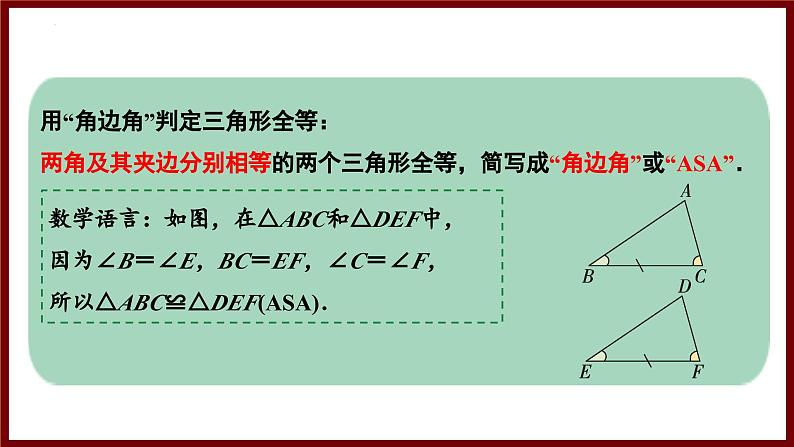
用“角边角”判定三角形全等：两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”．
数学语言：如图，在△ABC和△DEF中，因为∠B＝∠E，BC＝EF，∠C＝∠F，所以△ABC≌△DEF(ASA)．
例1 如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是( )
A．SSS B．SAS C．AAS D．ASA
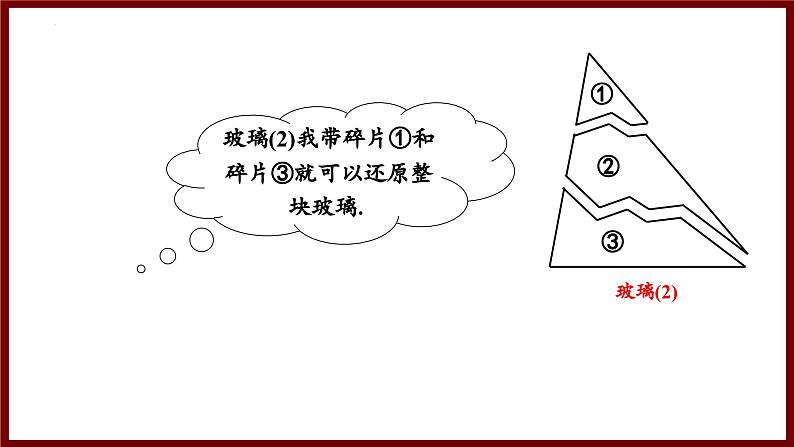
玻璃(2)我带碎片①和碎片③就可以还原整块玻璃.
具体做法：①作∠GEH=∠B；②在射线EH上截取EF=BC；③根据三角形内角和定理，计算出∠BCA的度数，并以F为顶点，以EF为一边，作∠EFD=∠BCA，另一边与EG交于点D.④量得∠EDF=∠A.
△DEF就是玻璃(2)的形状.
用“角角边”判定三角形全等：两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”．
数学语言：如图，在△ABC和△DEF中，因为∠B＝∠E，∠C＝∠F，AC＝DF，所以△ABC≌△DEF (AAS)．
例2 如图，已知∠1=∠2，若用“AAS”说明△ACB≌△BDA，还需添加条件( )
A．AD=BC B．BD=AC C．∠D=∠C D．OA=OB
1. 在△ABC与△A′B′C′中，已知∠A＝44°，∠B＝67°，∠C′＝69°，∠A′＝44°，且AC＝A′C′，那么这两个三角形( 　 )
A．一定不全等　 B．一定全等　 　C．不一定全等　　 D．以上都不对
2. 图中的两个三角形全等吗？请说明理由.
解：两个三角形全等；根据图中信息，三角形已经有两个角相等，且有一条边为公共边且为对应边，符合“角角边”的判定定理.
3. 如图，已知∠ACB=∠DBC，∠ABC=∠CDB，判断下面的两个三角形是否全等，并说明理由.
解：不全等，因为BC虽然是公共边，但不是对应边.
4. 已知：如图，点B，F，C，D在一条直线上，AB=ED， AB∥ED，AC∥EF. △ABC和△EDF全等吗，请说明理由.
解：△ABC和△EDF全等，理由如下：因为 AB∥ED，AC∥EF，所以∠B=∠D，∠ACB=∠EFD.
在△ABC与△EDF中，因为∠B=∠D，∠ACB=∠EFD，AB=ED，根据三角形全等的判定条件“AAS”，
可以得到△ ABC ≌△ EDF .
5. 如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C ，试说明：AD=AE.
解：在△ACD和△ABE中，
因为∠A=∠A ， AC=AB ，∠C=∠B，
可以得到△ACD≌△ABE.
根据三角形全等的判定条件“ASA”，
利用“角边角、角角边”判定三角形全等
用“ASA”判定三角形全等
用“AAS”判定三角形全等
两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”．
两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”．
数学语言：如图，在△ABC和△DEF中，因为∠B＝∠E，∠C＝∠F，AC＝DF，所以△ABC≌△DEF(AAS)．
知识点1　用“ASA”判定三角形全等
1. 如图，∠ABC＝∠DCB，若直接用“ASA”判定△ABC≌△DCB，则还需 添加的条件为(　D　)
2. 如图是小明家的装饰窗格，小明发现其中一块三角形玻璃坏了，需要重 新配一块，若需要给玻璃店的老板提供相关数据，才能重新配一块大小、 形状完全相同的新玻璃．小明将该三角形记作△ABC，则下列提供的信息 中，配出来的玻璃不．一．定．符合要求的是(　D　)
3. (教材随堂练习第1题改编)如图，点B，F，C，E在一条直线上，已知 ∠B＝∠E，BF＝CE，∠ACB＝∠DFE，试说明：△ABC≌△DEF.
知识点2　用“AAS”判定三角形全等
4. 如图，AO平分∠BAC，若直接用“AAS”判定△AOD≌△AOE，则还需 添加的条件为(　C　)
5. (教材随堂练习第1题改编)如图，已知∠DBC＝∠A＝90°，DE⊥AB于 点E，且BC＝BD，试说明：△DBE≌△BCA.
知识点3　已知两角及一边用尺规作三角形
6. 如图，已知△ABC，作∠MDN＝∠A，在射线DM上截取DE＝AB，以 点E为顶点，以ED为一边，作∠DEF＝∠B，EF交射线DN于点F，根据 上述作图步骤可得到△DEF≌△ABC，这种作一个三角形与已知三角形全 等的依据是 ⁠ ．
ASA（或两角及其夹边分别相等的两个三角形全等）
7. (教材素材改编)如图，已知∠α，∠β和线段a，若在△ABC中，∠B＝ ∠α，∠C＝∠β，BC＝2a，试用尺规作出△ABC(不写作法，保留作图痕 迹)．
8. 如图，已知∠ABD＝∠CBD，DB平分∠ADC，则下列结论一定成立的 是(　D　)
9. (教材例题改编)如图，在△ABC中，D，E分别是AB，AC边上一点，连 接DE并延长交AB的平行线CF于点F，若DE＝EF，AB＝7，CF＝5，则 BD的长度为(　B　)
10. 如图，在△ABC中，DE∥AB，DE＝AD，∠BDA＝∠CED，下列结 论：①△CDE≌△BAD；②∠C＝∠BAC；③AB＝CD；④∠CBA＝ ∠CAB． 其中正确的结论为______(填序号)．
11. 如图，在△ABC和△DEF中，∠C＝∠F，BC∥EF，点A，B，D，E 在同一条直线上，AD＝BE，试探究AC和DF的数量及位置关系，并说明 理由．
所以△ABC≌△DEF（AAS），所以AC＝DF，∠A＝∠FDE，所以AC∥DF，综上所述，AC＝DF且AC∥DF.
12. 如图，已知BF⊥AC，CE⊥AB，CE交BF于点D，AD平分∠BAC.
(1)试说明：△AFD≌△AED；
(2) 试说明：AB＝AC.
(1)当AD，A′D′分别是BC和B′C′边上的高线时，则AD＝A′D′.请补全下面 的解题思路；
解：（1）①∠ADB＝∠A'D'B'＝90°；②△ABD≌△A'B'D'；
13. (补充思路过程)如图，已知△ABC≌△A′B′C′.
(2)当AD与A′D′分别是∠BAC和∠B′A′C′的平分线时，请根据以上思路， 判断AD与A′D′的数量关系，并说明理由．